泰勒公式

一、泰勒公式

任何一个函数，都可以通过泰勒公式，表达成多项式的形式，在不同的小区域，多项式的系数不一样。
越高阶的项，系数越小（因为有阶乘）。

泰勒展开式

若 h(x) 在 x=_x_0 点的某个领域内有无限阶导数，那么在此领域内有：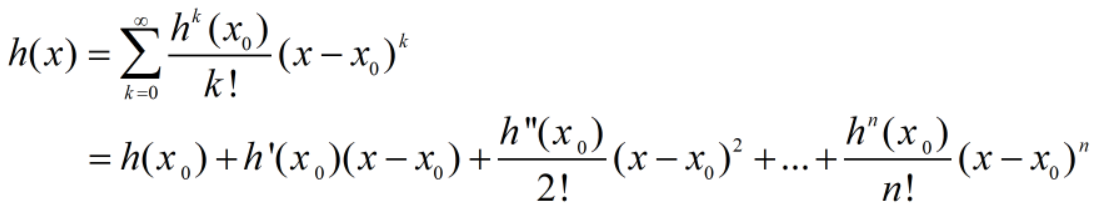

当 x 很接近 x_0 时，有 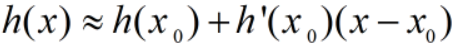，因为高次幂项都很小，可以忽略。
此时，函数 _h(x) 在 x=x_0 点附近关于 _x 的幂函数展开式，叫泰勒展开式。
【举例】
在 x 很接近 π/4的地方展开，函数曲线和原函数曲线有重合的部分。

多变量泰勒展开式

二、泰勒公式与神经网络

sigmoid存在n阶导数，sigmoid的泰勒展开，可以由无穷多项式表达。
通过神经元的一层，输出是一组序列（组数是神经元的个数），每个序列都可以展开为一个多项式。
神经网络的输出Y，本质是X的多项式，多项式系数由各个参数决定。

一层神经元网络，只要神经元足够多，学习时间足够长，可以拟合任意函数；但实际上并不容易拟合。
原因：1.神经元多，学习时间长，算力跟不上。2.高阶项不容易拟合。
例如：假设一个激活函数是平方函数：f(x)=(wx+w0)^2，该函数的三阶及以上导数为0，所以就无法拟合四阶函数。

神经网络越深，高阶项更容易出现大数值，更快的产生高阶项；激活函数（非线性），决定了高阶项。因为线性函数的二阶及以上导数为0，多层神经元叠加也无法出现高阶项。理论上讲，Relu的高阶项能力较弱，但通过Relu可以把神经网络做的很深，整体上效果也比较好。
最终是模型和待解决问题复杂度的匹配问题。
待解决问题，是一个函数（具体形式未知），问题的复杂程度，取决于函数高阶项。
机器学习的模型，也是一个函数（具体形式可知，但很复杂）。
待解决问题 VS 模型 的二维象限。
为什么需要高阶项？
实际问题中，待解决问题，都是复杂函数，高阶项很多。

机器学习模型的特点：
1.曲线平滑，输入轻微变化，输出也是轻微变化，不会导致输出的剧烈震荡。
从这点看，NLP难度远大于图像、声音处理。
很多业务场景中，人为规定的规则，项目有大量不平滑的问题，需要有一套规则系统。