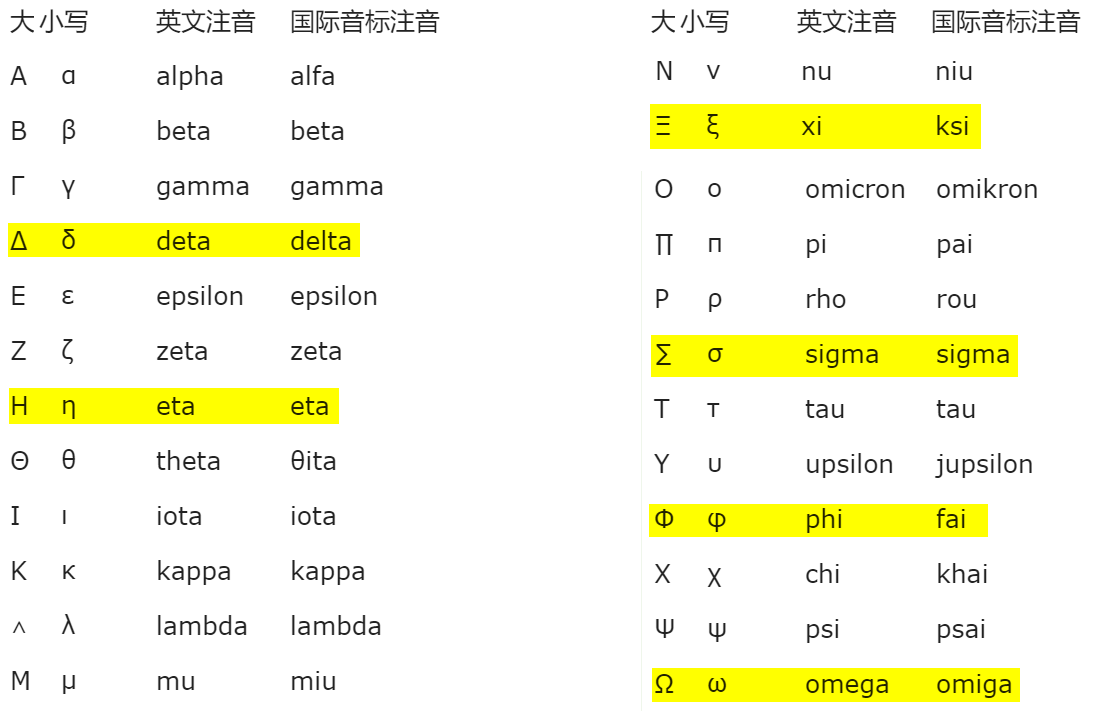
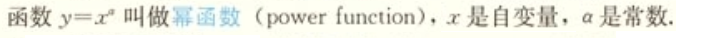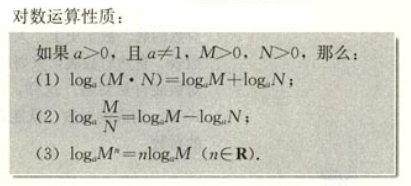1.符号、定义

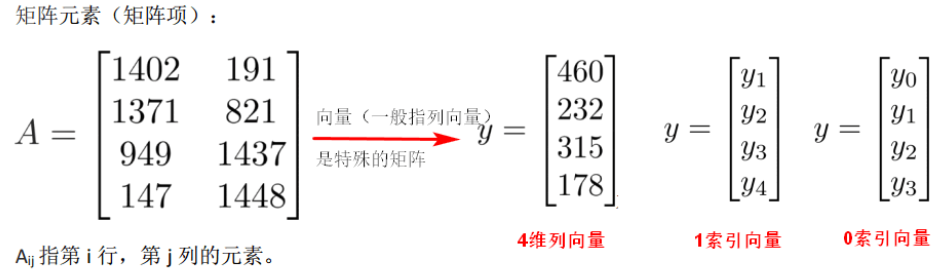
image.png
image.png

1.1根式

image.png

1.2对数

image.png

1.3向量

image.png
image.png

1.4导数

image.png
image.png

1.5定积分

image.png

1.6微积分

image.png
image.png

1.7偏导数

image.png
偏导数的几何意义：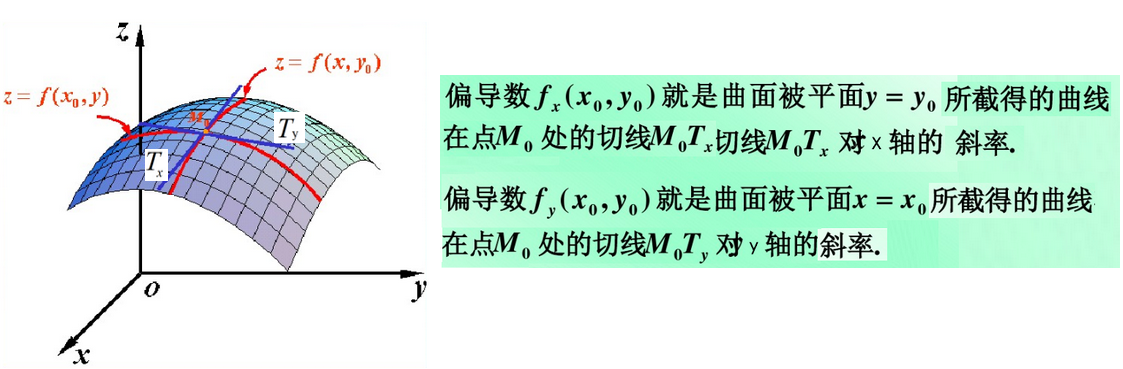
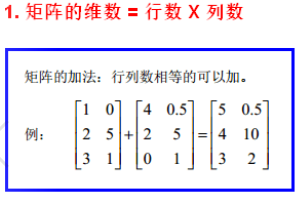
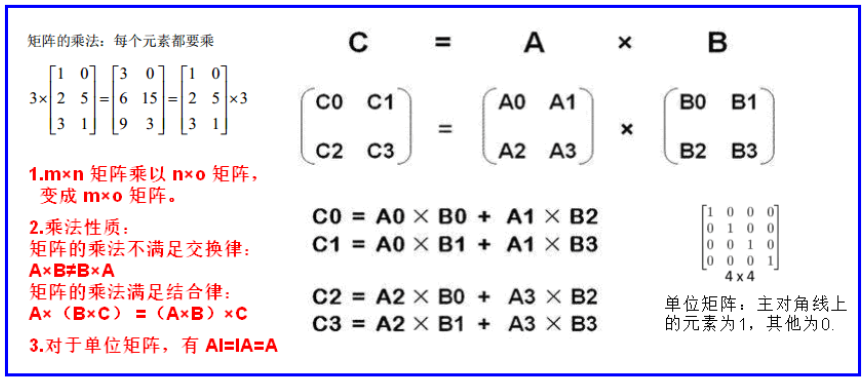
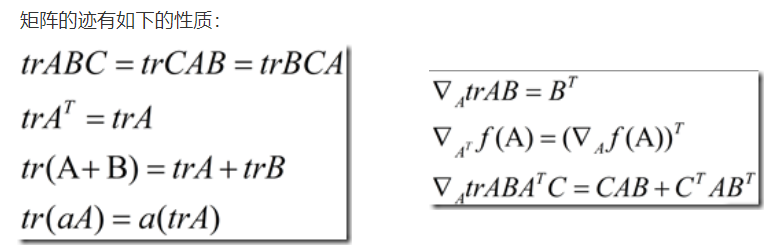
image.png

1.8 矩阵

矩阵的迹：在线性代数中，一个n×n矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵
A的迹（或迹数），一般记作tr(A)。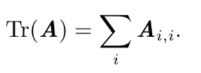数学基础知识 - 图14

image.png

矩阵与向量
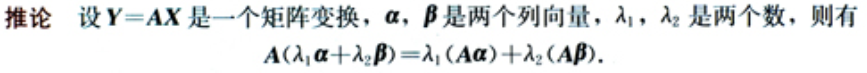
image.png
image.png

二阶矩阵变换
image.png

1.9 标准差

量化数据离散程度的方法：

  • 极差 = 最大值 — 最小值。但只有两个数据来评判一组数据，是不科学的。
  • 离均差 (deviation from mean)= 数据 — 均值。因为离散度是数据偏离均值的程度，可以将离均差累加，来衡量离散程度；但离均差有正有负，所以一般用离均差的绝对值之和，或离均差的平方和，衡量离散程度。

  • 方差（variance）：离均差平方和的平均值。离均差的平方和的大小和样本数量有关，为了增加可比性，对离均差的平方和求平均值。（之所以除以n-1而不是除以n，是因为这样能使我们以较小的样本集更好的逼近总体的标准差，即统计上所谓的“无偏估计”。）

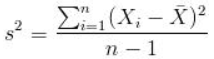
    image.png

  • 标准差：方差的算术平方根。方差是数据的平方，与检测值本身相差较大，所以用方差开根号来衡量离散度。

    1.            ![image.png](https://cdn.nlark.com/yuque/0/2019/png/317160/1557760718827-d0c03087-1449-41a5-a347-46706c777637.png#align=left&display=inline&height=91&name=image.png&originHeight=114&originWidth=268&size=9447&status=done&style=none&width=214.4)

  • 协方差（covariance）：协方差用于衡量两个变量的总体误差，方差是协方差的特殊情况（两个变量相同）。两个变量的变化趋势一致，协方差是正值；两个变量的变化趋势相反，协方差是负值；如果协方差是0，就是统计上讲的“相互独立”。期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为：

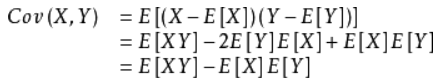
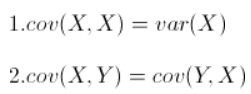
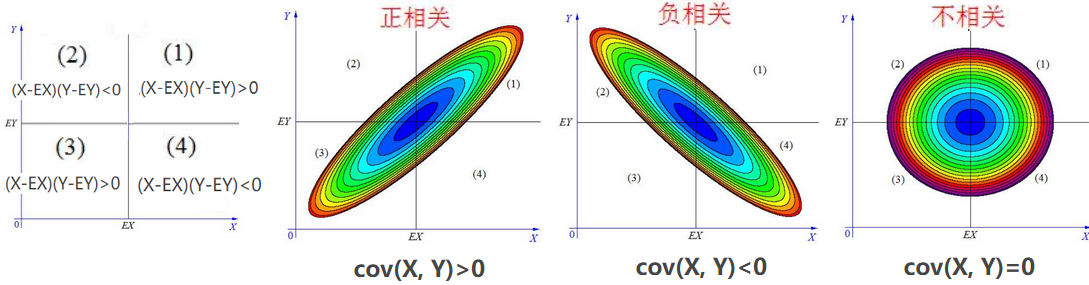
    image.png image.png
    image.png

方差variance 协方差covariance
度量数据离散程度。
描述一维数据。		 度量两个随机变量之间的关系/相关性，
描述二维数据。
描述多维数据（协方差矩阵）。
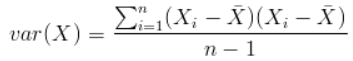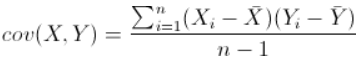image.png image.png

2.公式、定理、性质

2.1对数

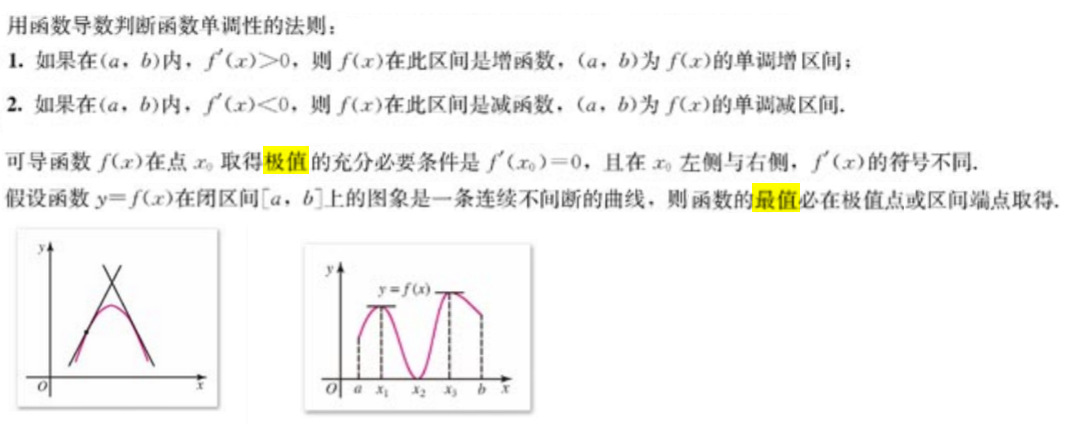
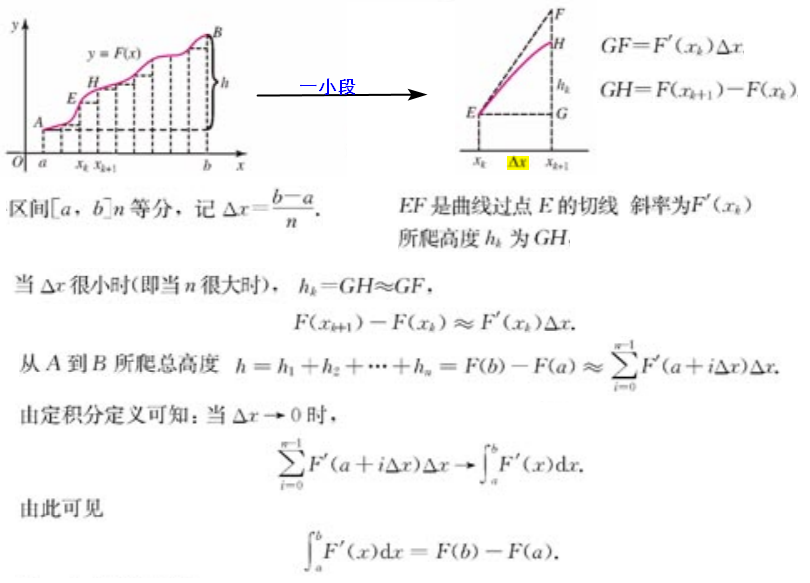
image.png

2.2导数、积分

【问题引出】求函数曲线的切线？求曲线形的面积？
【基本思想】求导和求积分是互为逆运算，运算的对象是函数/曲线，求导和求积分的基本思想是以直代曲、用高倍放大镜观察一条曲线的微小片段。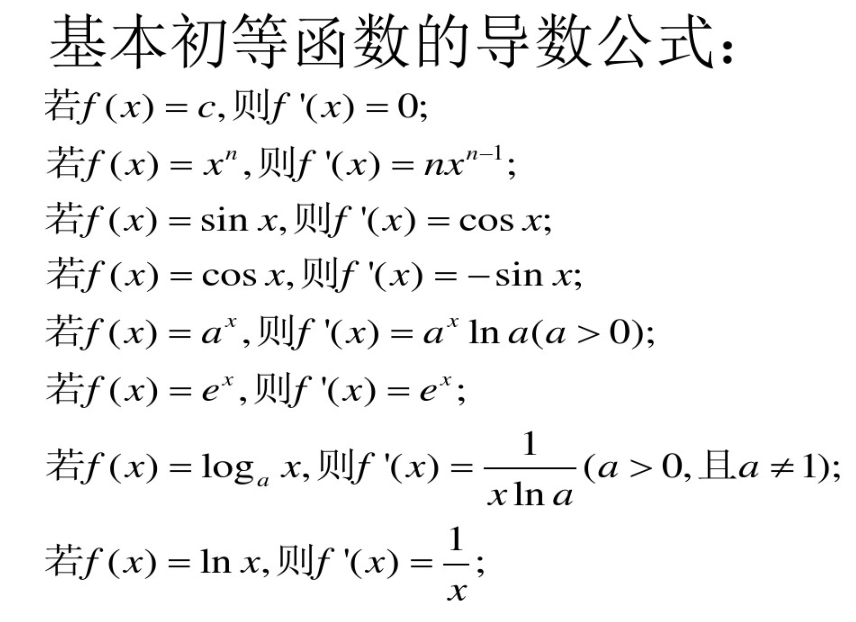
image.png
image.png
image.png image.png

2.2.1矩阵的导数

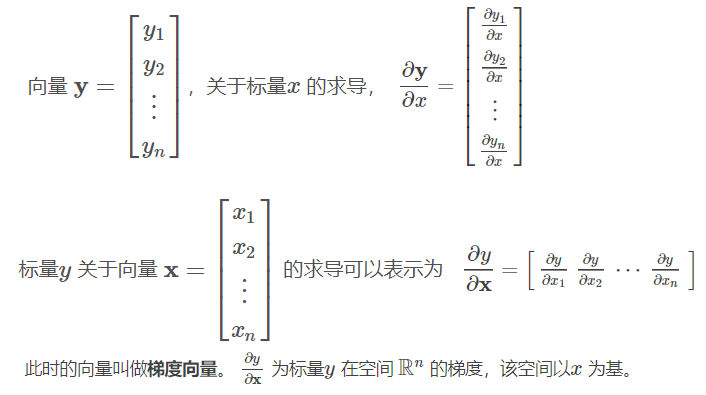
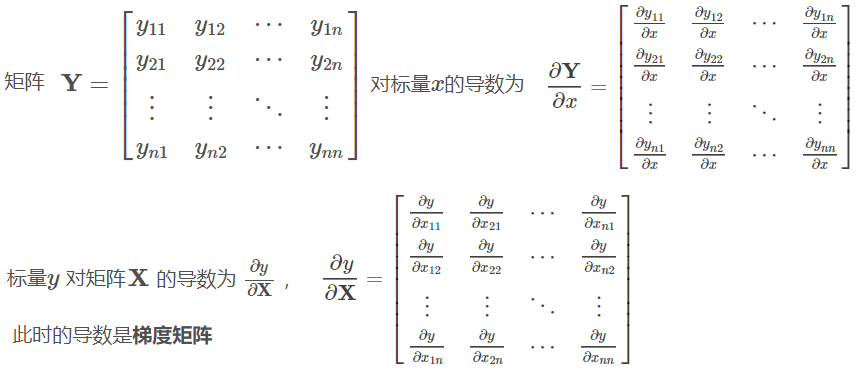
image.png
image.png

2.3高阶偏导数

image.png
image.png

2.4矩阵

image.png
image.png
image.png
image.png
image.png
image.png

3.函数

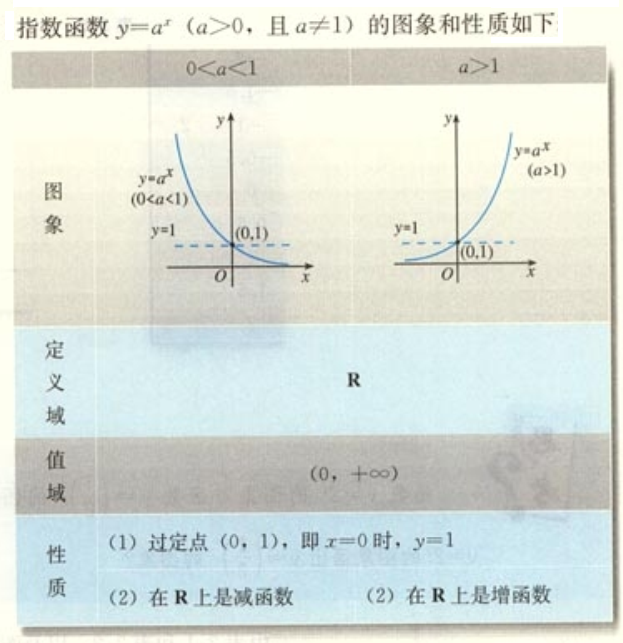
3.1指数函数

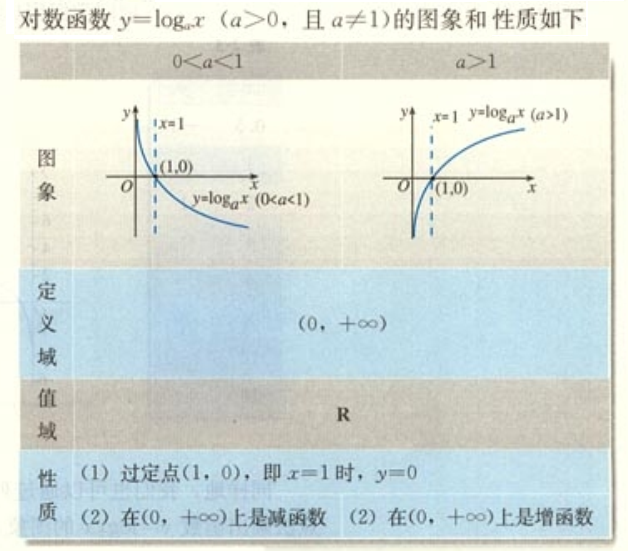
image.png

3.2对数函数

image.png

3.3幂函数

image.png