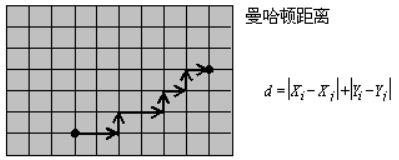
【注意】
- 计算两点的距离时,要保证两者的维数相等。
- 距离,本质上是两个同维事物在差异上的度量。
【总结】
| 范围 | 度量 | |
|---|---|---|
| 欧式距离 | 两点间的距离(直线距离) | |
| 曼哈顿距离 | 两点间的距离(非直线距离) | |
| 海明距离 | 衡量不同位的差异 | |
| 角度距离 | 衡量两点与原点之间连线的夹角 |
一、用长度度量
1.欧式距离(Euclidean Distance)
将样本的特征看做空间维度,
若有n个特征值的两点为: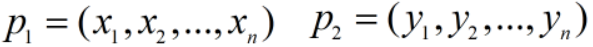 ,
,
则两点间的欧式距离为: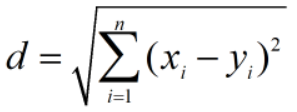
修正欧式距离
由欧式距离公式可知,当维数越多时,距离会越大;因此当样本的维数不一致时(例如:有的样本在某些维度上缺失数值),会造成距离误差(即共同的维数越高,计算出的距离越大)。因此,需要消除维数带来的差异。
修正欧式距离: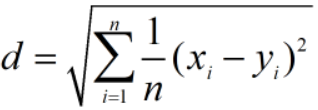
【示例】
| 观众电影评分表 | ||||
|---|---|---|---|---|
| 阿甘正传 | 阿凡达 | 让子弹飞 | 赎罪 | |
| A | 5 | 4 | 6 | 3 |
| B | 4 | 6 | - | - |
| C | 6 | 4 | 5 | 5 |
B有维度数值缺失,A和B的距离为:d=sqrt[1/2(5-4)^2+1/2(4-6)^2]=1.58,
A和C的距离为:d=sqrt[1/4(5-6)^2+1/4(4-4)^2+1/4(6-5)^2+1/4(3-5)^2]=1.22
所以,A和C的差异更小。
权重欧式距离
当n个维度上都有权重w时(衡量各个维度的重要性),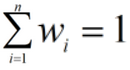
对于两点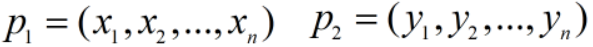 ,
,
修正权重的欧式距离为: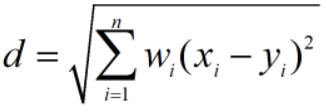
修正欧式距离是权重欧式距离的一个特例,即权重欧式距离在各个维度上的权重都为1/n。
修正权重
当有维度缺失的情况时,已有维度的权重不再满足相加为1,即 ,
,
此时需要进行权重归一化(当前权重除以参与计算的权重之和):
| 观众电影评分表 | ||||
|---|---|---|---|---|
| 阿甘正传 | 阿凡达 | 让子弹飞 | 赎罪 | |
| A | 5 | 4 | 6 | 3 |
| B | 4 | 6 | - | - |
| 原权重 | 0.3 | 0.2 | 0.4 | 0.1 |
| 修正权重 | 0.8 | 0.2 |
修正特征数值
不同的特征项,在实际意义中,是存在数值差异的;在计算距离时,距离受数值差异较大的特征项的影响更大,所以需要对数值进行修正。
特征a上修正的特征数值 = 特征a上原有的特征值/该特征上的均值
【示例】
| 身高(cm) | 体重(kg) | |
|---|---|---|
| A | 168 | 62 |
| B | 178 | 65 |
| 修正数值: | 平均身高172 | 平均体重62 |
| A | 168/172=0.98 | 62/62=1 |
| B | 178/172=1.03 | 65/62=1.05 |
2.曼哈顿距离(Manhattan Distance)
3.海明距离(Hamming distance)
在信息编码中,两个合法代码对应位上编码不同的位数称为码距(即对应位上相同为0,不同为1),又称海明距离。海明距离的本质是异或运算。
例如:,有3个位置上的编码不同,海明距离为3。
海明距离是曼哈顿距离的一个特例,即当曼哈顿距离中,每一维都取值0或1时。
二、用角度度量
1.角度度量
- 角度的度量对长度(长度即度量点到原点的距离)不敏感。
- 角度度量更多是衡量各维度在比例上的差异,和绝对数值关系不大。
相似度
角度参与计算,使用反余弦函数(代表相似度,角度越小,相似度越大):
对于n个维度的两点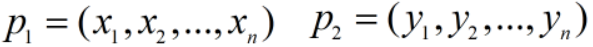 ,角度度量:
,角度度量:
相似度为:, 当
时,
分母其实是两点分别到原点的距离的乘积,可以看做是消除了长度的影响,因为角度度量对长度不敏感,只要各个对应的维度是成相同比例的,相似度就不变。
【示例】
假设上述数据中的隐藏信息为:男性普遍的兴趣在军事频道,不在美容频道;而女性普遍的兴趣在美容频道,不在军事频道。因此每个男性/女性用户在各个频道上的花销是存在比例差异的,此时用角度度量,可以计算出同一性别的用户的相似度更高。