11. 盛最多水的容器

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明：你不能倾斜容器，且 n 的值至少为 2。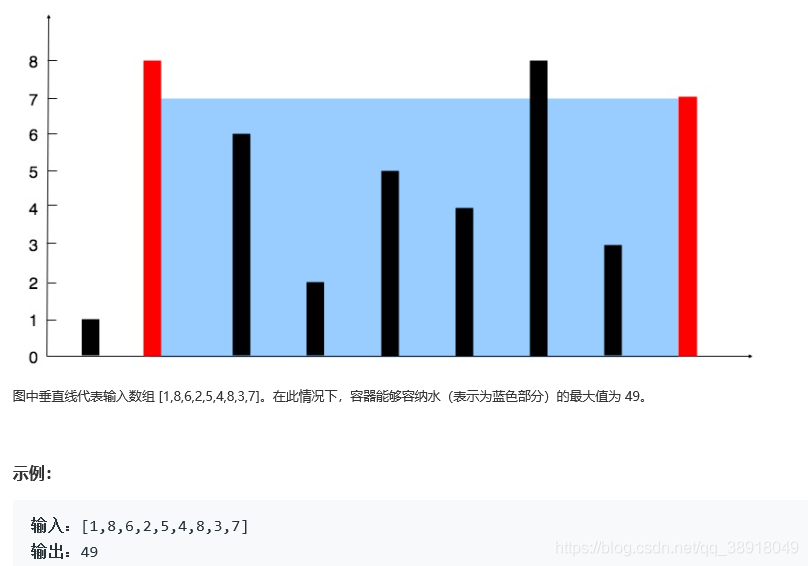

法一：最优的双指针
比较好理解的思路，左右两边的柱子往中间靠，保留最大值。
时间复杂度：O(N)，双指针总计最多遍历整个数组一次。
空间复杂度：O(1)，只需要额外的常数级别的空间

class Solution {
    public int maxArea(int[] height) {
        int left = 0;
        int right = height.length-1;
        int res = 0;
        while (left < right) {
            int area = (right - left) * Math.min(height[left], height[right]);
            res = Math.max(res, area);
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        return res;
    }
}

法二:不推荐暴力法
时间复杂度：o（n平方）

// 暴力法，不推荐
class Solution {
    public int maxArea(int[] height) {
        int area = 0;
        int max = 0;
        for (int i=0; i<height.length-1; i++) {
            for (int j=i+1; j<height.length; j++) {
                area = (j - i) * Math.min(height[i], height[j]);
                if (area > max) {
                    max = area;
                }
            }
        }
        return max;
    }
}