99. 恢复二叉搜索树

题目：

给你二叉搜索树的根节点 root ，该树中的两个节点被错误地交换。请在不改变其结构的情况下，恢复这棵树。
进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用常数空间的解决方案吗？

示例 1：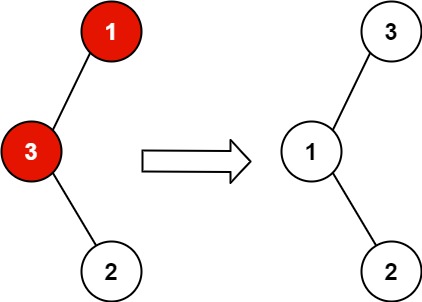

输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

示例 2：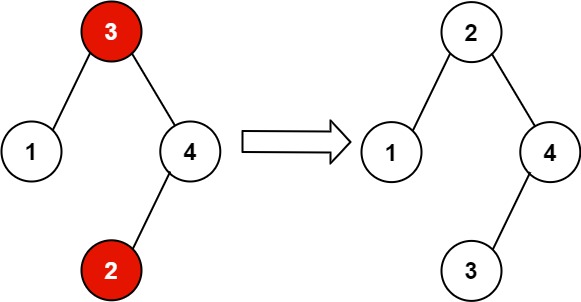

输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

提示：
树上节点的数目在范围 [2, 1000] 内
-231 <= Node.val <= 231 - 1

解答：

这道题难点，是找到那两个交换节点，把它交换过来就行了。
这里我们二叉树搜索树的中序遍历(中序遍历遍历元素是递增的)
如下图所示，中序遍历顺序是 4,2,3,1，我们只要找到节点 4 和节点 1 交换顺序即可！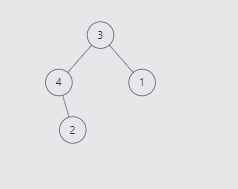

这里我们有个规律发现这两个节点：

• 第一个节点，是第一个按照中序遍历时候前一个节点大于后一个节点，我们选取前一个节点，这里指节点 4；
• 第二个节点，是在第一个节点找到之后，后面出现前一个节点大于后一个节点，我们选择后一个节点，这里指节点 1；

对于中序遍历，我们有两种方法。

• 方法一：迭代
• 方法二：递归

//方法一：迭代
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public void recoverTree(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode firstNode = null;
        TreeNode secondNode = null;
        TreeNode pre = new TreeNode(Integer.MIN_VALUE);
        TreeNode p = root;
        while (p != null || !stack.isEmpty()) {
            while (p != null) {
                stack.push(p);
                p = p.left;
            }
            p = stack.pop();
            if (firstNode == null && pre.val > p.val) firstNode = pre;
            if (firstNode != null && pre.val > p.val) secondNode = p;
            pre = p;
            p = p.right;
        }
        int tmp = firstNode.val;
        firstNode.val = secondNode.val;
        secondNode.val = tmp;
    }
}

//方法二：递归
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    TreeNode firstNode = null;
    TreeNode secondNode = null;
    TreeNode preNode = new TreeNode(Integer.MIN_VALUE);
    public void recoverTree(TreeNode root) {
        in_order(root);
        int tmp = firstNode.val;
        firstNode.val = secondNode.val;
        secondNode.val = tmp;
    }
    private void in_order(TreeNode root) {
        if (root == null) return;
        in_order(root.left);
        if (firstNode == null && preNode.val > root.val) firstNode = preNode;
        if (firstNode != null && preNode.val > root.val) secondNode = root;
        preNode = root;
        in_order(root.right);
    }
}