1.   图是较线性表和树更为复杂的数据结构，因此和线性表、树对节点的定义有所不同。在本章中主要是介绍图结构在计算机中的具体实现。

图的概述

图的基本概念

图是一种数据结构，其中结点可以具有零个或多个相邻元素。两个结点之间的连接称为边。结点也可以称为顶点。
概念为：由顶点（Vertex）集和边( Edge）集组成， 记为G＝（V，E）,其中V 是有穷非空集合，称为顶点集，v ∈V称为顶点。E是有穷集合，称为边集， e∈E 称为边。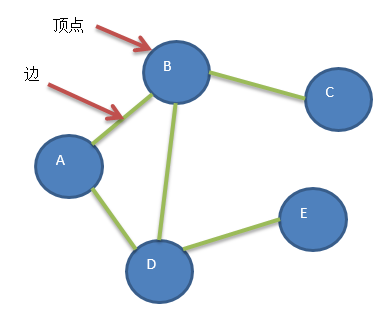
image.png

为什么要有图

1)前面我们学了线性表和树
2)线性表局限于一个直接前驱和一个直接后继的关系
3)树也只能有一个直接前驱也就是父节点
4)当我们需要表示多对多的关系时， 这里我们就用到了图

几种常见图

  • 在图中，如果代表边的顶点对（或序偶）是无序的，则称为无向图。无向图中代表边的无序顶点对通常用圆括号括起来，用以表示一条无向边。如(i，j)表示顶点i与顶点j的一条无向边，显然，(i，j)和(j，i)所代表的是同一条边。

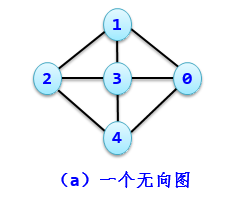
image.png

  • 如果表示边的顶点对（或序偶）是有序的，则称为有向图。在有向图中代表边的顶点对通常用尖括号括起来，用以表示一条有向边（又称为弧），如表示从顶点i到顶点j的一条边。

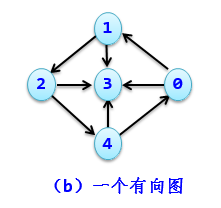
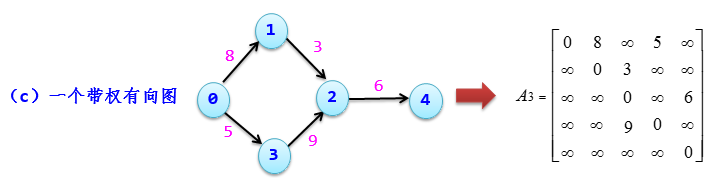
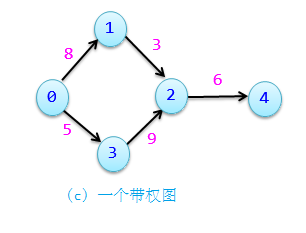
image.png

  • 图中每一条边都可以附有一个对应的数值，这种与边相关的数值称为权。权可以表示从一个顶点到另一个顶点的距离或花费的代价。边上带有权的图称为带权图

image.png

图的基本术语

  • 在一个无向图中，若存在一条边(i，j)，则称顶点i和顶点j为该边的两个端点，并称它们互为邻接点，即顶点i是顶点j的一个邻接点，顶点j也是顶点i的一个邻接点。
  • 在一个有向图中，若存在一条边，则称此边是顶点i的一条出边，同时也是顶点j的一条入边。i和j分别为此边的起始端点（简称为起点）和终止端点（简称终点）。并称顶点j是i的出边邻接点，顶点i是j的入边邻接点。
  • 在无向图中，顶点所具有的边的数目称为该顶点的度。在有向图中，顶点i的度又分为入度和出度，以顶点i为终点的入边的数目，称为该顶点的入度。以顶点i为起点的出边的数目，称为该顶点的出度。一个顶点的入度与出度的和为该顶点的度。
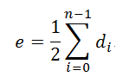
  • 若一个图（无论有向图或无向图）中有n个顶点和e条边，每个顶点的度为di（0≤i≤n-1），则有：image.png


  • 图的存储结构

    邻接矩阵

    邻接矩阵是表示顶点之间邻接关系的矩阵。设G=(V，E)是含有n（设n>0）个顶点的图，各顶点的编号为0～n-1，则G的邻接矩阵数组A是n阶方阵。
    （所谓邻接矩阵，就是一个反应边与边之间联系的一个二维数组。这个二维数组我们使用A[n][n]来表示，其中 n 是顶点数。）

  • 如果是不带权图，则二维数组中的每一个元素的值根据是否有边，设置为 0 或 1：

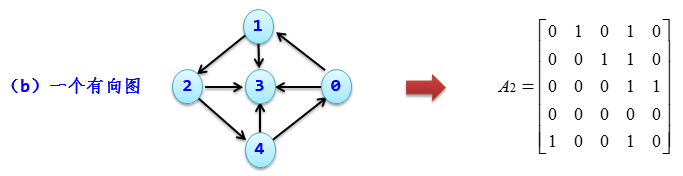
image.png

  • 如果是带权图，则：

image.png

邻接矩阵表述形式

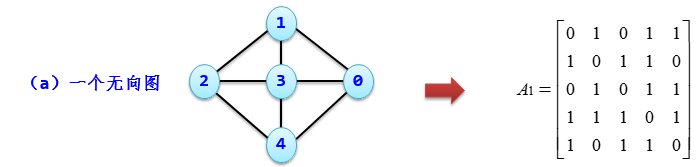
image.png
可以这样理解上图：
第一行表示：0 顶点与 1、3、4 顶点有边，与自身和 2 顶点没有边
第二行表示：1 顶点与 0、2、3 顶点有边，与自身和 4 顶点没有边
第三行表示：2 顶点与 1、3、4 顶点有边，与自身和 0 顶点没有边
… …
image.png
image.png