141. 环形链表

给定一个链表，判断链表中是否有环。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。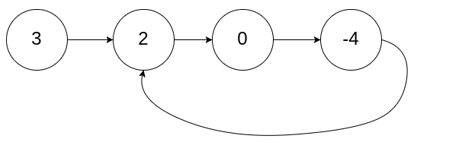

示例 2：
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。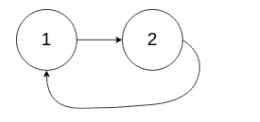

示例 3：
输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

进阶：
你能用 O(1)（即，常量）内存解决此问题吗？
法一：快慢指针
时间复杂度：O(n)，让我们将 nnn 设为链表中结点的总数。为了分析时间复杂度，我们分别考虑下面两种情况。
空间复杂度：O(1)，我们只使用了慢指针和快指针两个结点，所以空间复杂度为 O(1)。

public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) return false;
        ListNode slow = head;
        ListNode fast = head.next;
        while (slow != fast) {
            if (fast == null || fast.next == null ) return false;
            slow = slow.next;
            fast = fast.next.next;
        }
        return true;
    }
}

法二：哈希表
时间复杂度：O(n)，对于含有 n 个元素的链表，我们访问每个元素最多一次。添加一个结点到哈希表中只需要花费 O(1) 的时间。
空间复杂度：O(n)，空间取决于添加到哈希表中的元素数目，最多可以添加 n个元素。

public class Solution {
    public boolean hasCycle(ListNode head) {
        HashSet<ListNode> set = new HashSet<>();
        while (head != null) {
            if (set.contains(head)) return true;
            set.add(head);
            head = head.next;
        }
        return false;
    }
}