1.    如果说深度优先遍历是在一个方向上“一头扎到底”，那么广度优先遍历则恰恰相反：先在各个方向上各走出1步，再在各个方向上走出第2步、第3步……一直到各个方向全部走完。听起来有些抽象，下面让我们通过二叉树的**层序遍历**，来看一看广度优先是怎么回事。<br />       层序遍历，顾名思义，就是二叉树按照从根节点到叶子节点的层次关系，一层一层横向遍历各个节点。<br />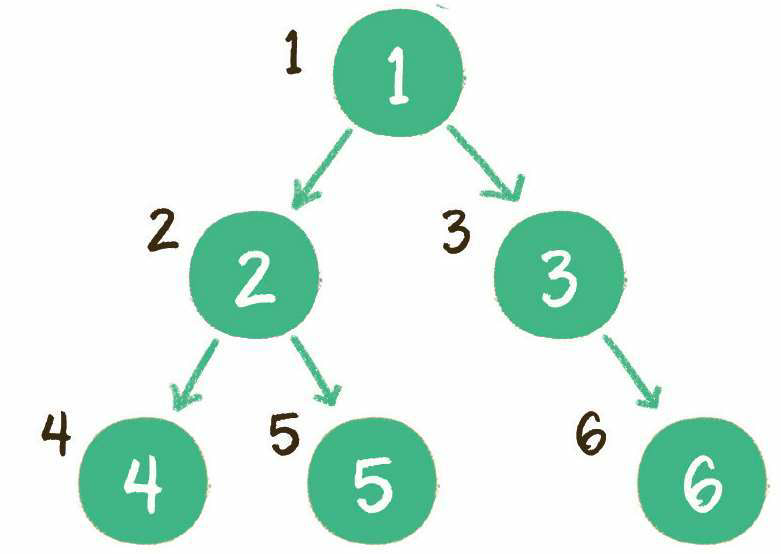![image.png](https://cdn.nlark.com/yuque/0/2021/png/955151/1612856386554-bdf87963-7767-4184-981d-7ac4fc0c9203.png#height=138&id=x3bEY&margin=%5Bobject%20Object%5D&name=image.png&originHeight=554&originWidth=781&originalType=binary&ratio=1&size=215720&status=done&style=none&width=195)<br />上图就是一个二叉树的层序遍历，每个节点左侧的序号代表该节点的输出顺序。<br />可是，二叉树同一层次的节点之间是没有直接关联的，如何实现这种层序遍历呢？<br />这里同样需要借助一个数据结构来辅助工作，这个数据结构就是队列。

详细遍历步骤如下：

  1. 根节点1进入队列。
    image.png
    2. 节点1出队，输出节点1，并得到节点1的左孩子节点2、右孩子节点3。让节点2和节点3入队。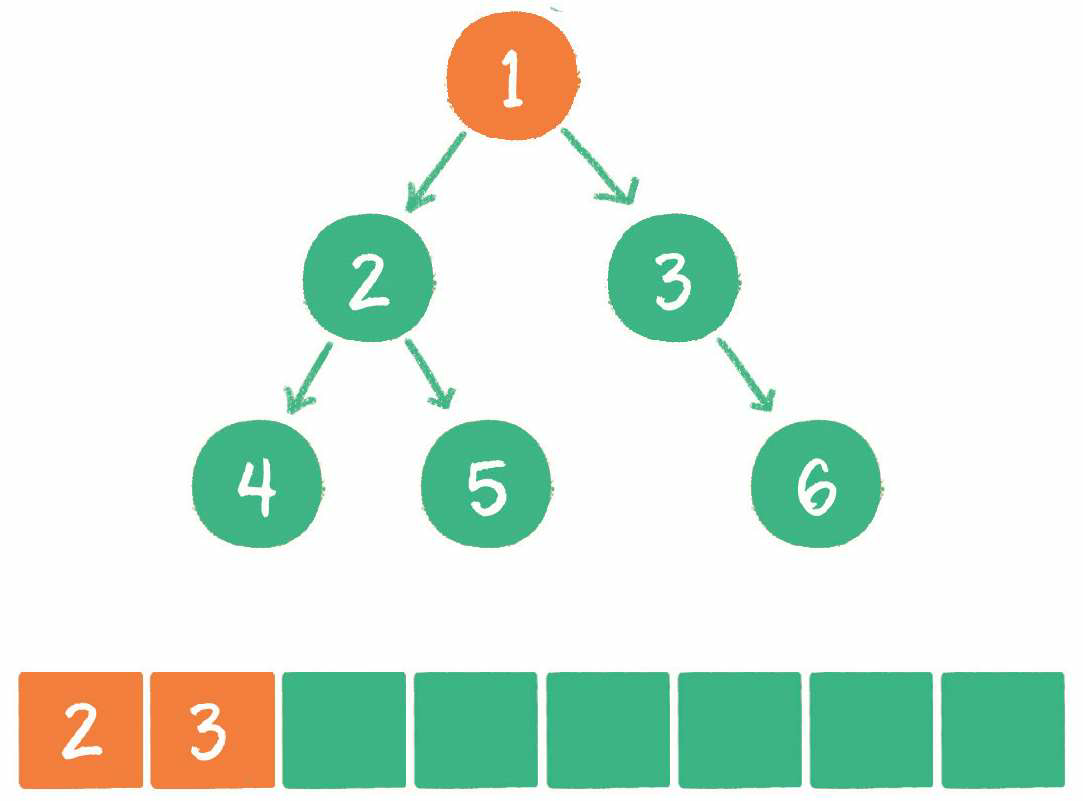
    image.png
    3. 节点2出队，输出节点2，并得到节点2的左孩子节点4、右孩子节点5。让节点4和节点5入队。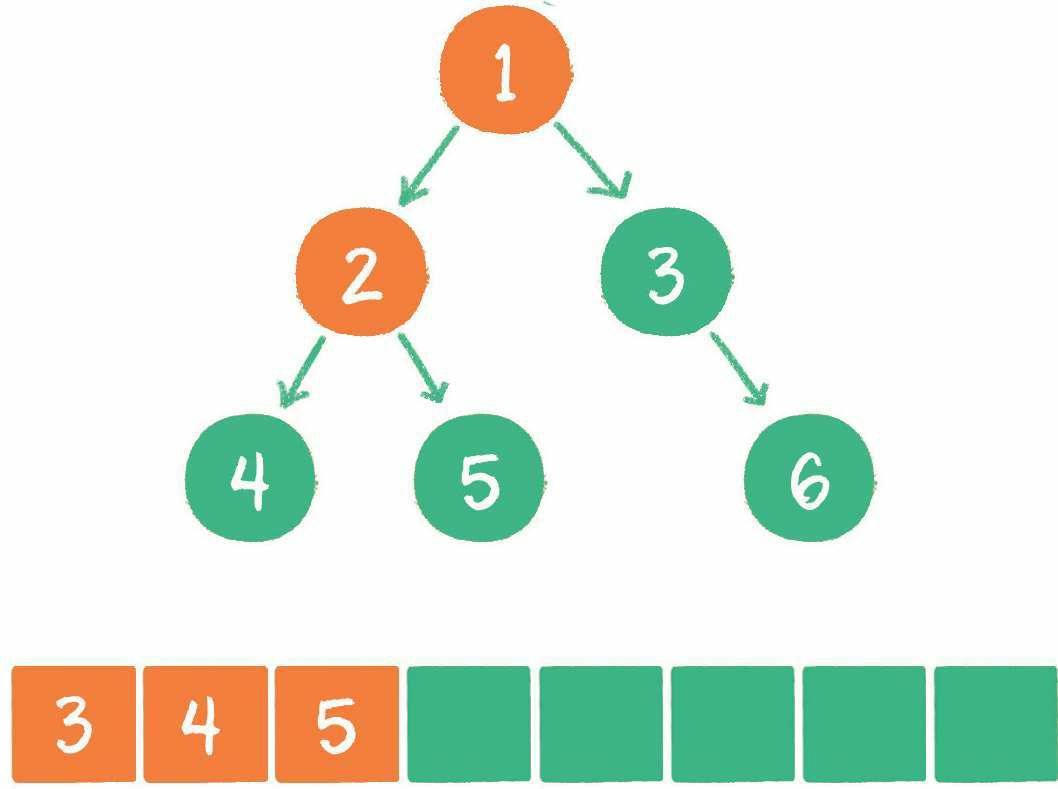
    image.png
    4. 节点3出队，输出节点3，并得到节点3的右孩子节点6。让节点6入队。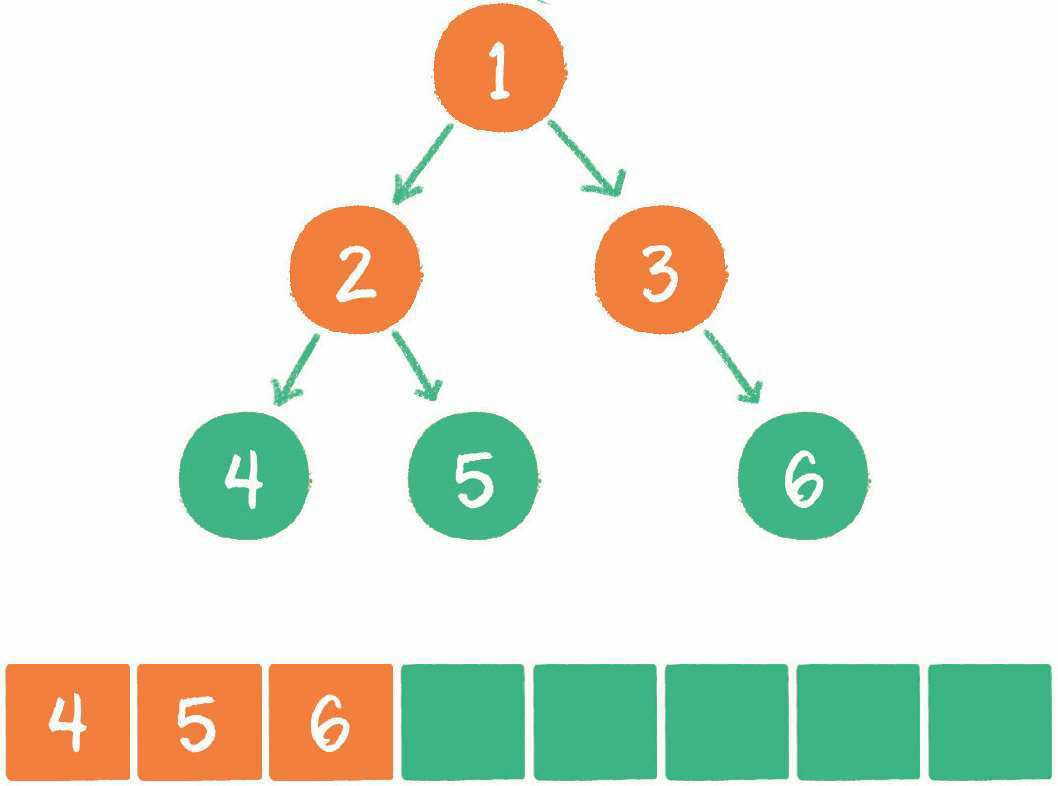
    image.png
    5. 节点4出队，输出节点4，由于节点4没有孩子节点，所以没有新节点入队。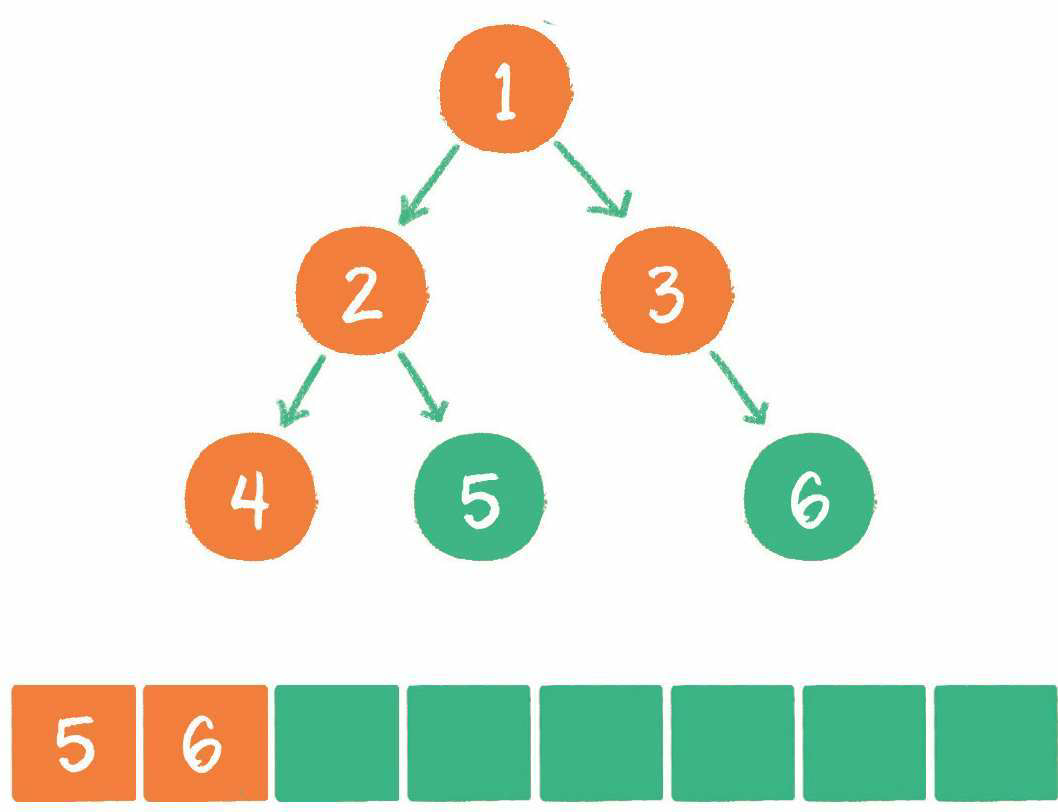
    image.png
    6. 节点5出队，输出节点5，由于节点5同样没有孩子节点，所以没有新节点入队。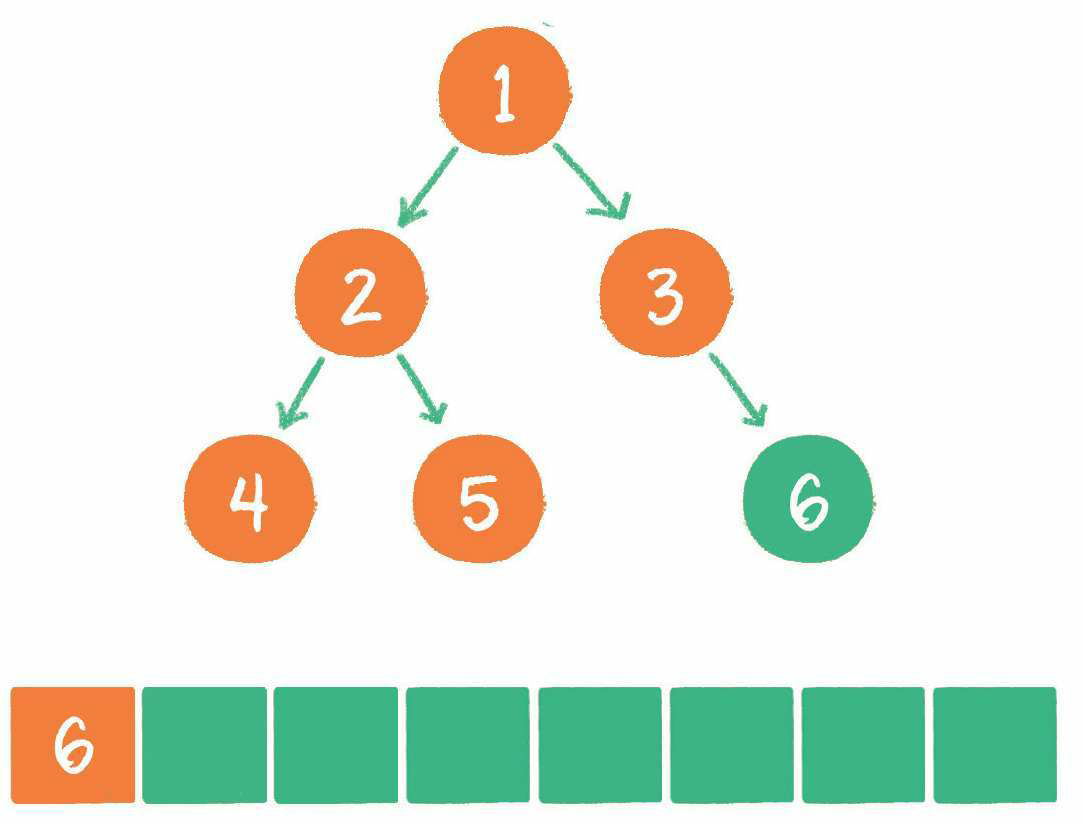
    image.png
    7. 节点6出队，输出节点6，节点6没有孩子节点，没有新节点入队。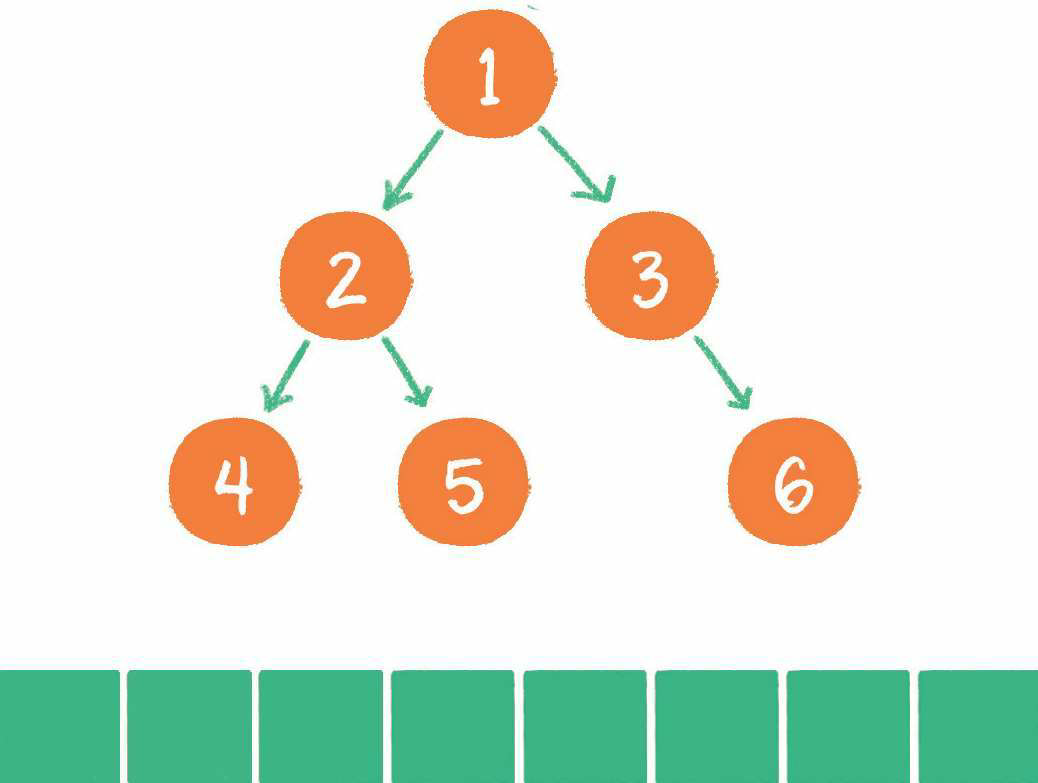
    image.png
    到此为止，所有的节点都遍历输出完毕。

实现代码

  1. /**
  2.   * 二叉树层序遍历
  3.   */
  4. import java.util.LinkedList;
  5. import java.util.Queue;
  7. class TreeNode {
  8.     int value;
  9.     TreeNode left;
  10.     TreeNode right;
  12.     TreeNode(int value) {
  13.         this.value = value;
  14.     }
  15. }
  17. public class Test {
  18.     public static void main(String[] args) {
  19.         TreeNode[] node = new TreeNode[10];// 以数组形式生成一棵完全二叉树
  20.         for (int i = 0; i < 10; i++) {
  21.             node[i] = new TreeNode(i);
  22.         }
  23.         for (int i = 0; i < 10; i++) {
  24.             if (i * 2 + 1 < 10)
  25.                 node[i].left = node[i * 2 + 1];
  26.             if (i * 2 + 2 < 10)
  27.                 node[i].right = node[i * 2 + 2];
  28.         }
  29.         // 广度优先遍历（也叫层序遍历）
  30.         levelOrderTraversal(node[0]);
  31.     }
  33.     public static void levelOrderTraversal(TreeNode biTree) {
  34.         Queue<TreeNode> queue = new LinkedList<TreeNode>();
  35.         //offer方法：向队列尾部插入元素（越界时返回假）
  36.         queue.offer(biTree);
  37.         while (!queue.isEmpty()) {
  38.             //poll方法：从队列头部删除元素（队列为空时返回null）
  39.             TreeNode node = queue.poll();
  40.             System.out.print(node.value + " ");
  41.             if (node.left != null) {
  42.                 queue.offer(node.left);
  43.             }
  44.             if (node.right != null) {
  45.                 queue.offer(node.right);
  46.             }
  47.         }
  48.     }
  49. }