一、队列的概述
要弄明白什么是队列,我们同样可以用一个生活中的例子来说明。<br />假如公路上有一条单行隧道,所有通过隧道的车辆只允许从隧道入口驶入,从隧道出口驶出,不允许逆行。<br /><br />因此,要想让车辆驶出隧道,只能按照它们驶入隧道的顺序,先驶入的车辆先驶出,后驶入的车辆后驶出,任何车辆都无法跳过它前面的车辆提前驶出。<br />
队列(queue)是一种线性数据结构,它的特征和行驶车辆的单行隧道很相似。不同于栈的先入后出,队列中的元素只能先入先出(First In First Out,简称FIFO)。队列的出口端叫作队头(front),队列的入口端叫作队尾(rear)。
我们把向队列中插入元素的过程称为入队(Enqueue),删除元素的过程称为出队(Dequeue)并把允许入队的一端称为队尾,允许出队的一端称为队头,没有任何元素的队列则称为空队。其一般结构如下:<br />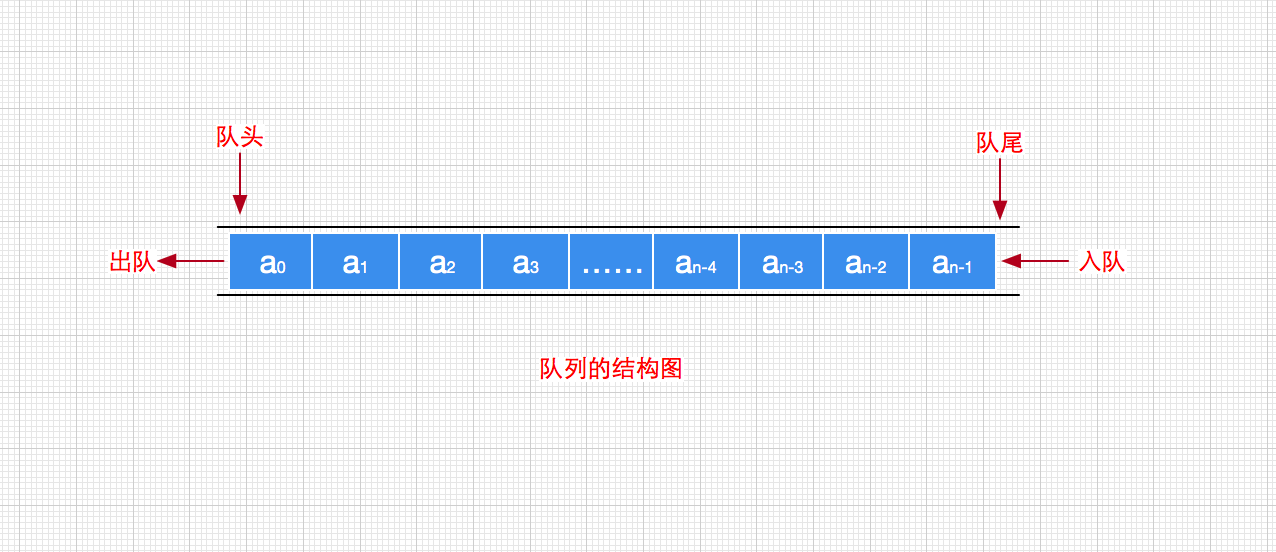
二、队列功能说明
关于队列的操作,我们这里主要实现入队,出队,判断空队列和清空队列等操作,声明队列接口Queue(队列抽象数据类型)如下:
/**
* 队列抽象数据类型
*/
public interface Queue<T> {
/**
* 返回队列长度
* @return
*/
int size();
/**
* 判断队列是否为空
* @return
*/
boolean isEmpty();
/**
* data 入队,添加成功返回true,否则返回false,可扩容
* @param data
* @return
*/
boolean add(T data);
/**
* offer 方法可插入一个元素,这与add 方法不同,
* 该方法只能通过抛出未经检查的异常使添加元素失败。
* 而不是出现异常的情况,例如在容量固定(有界)的队列中
* NullPointerException:data==null时抛出
* @param data
* @return
*/
boolean offer(T data);
/**
* 返回队头元素,不执行删除操作,若队列为空,返回null
* @return
*/
T peek();
/**
* 返回队头元素,不执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
T element();
/**
* 出队,执行删除操作,返回队头元素,若队列为空,返回null
* @return
*/
T poll();
/**
* 出队,执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
T remove();
/**
* 清空队列
*/
void clearQueue();
}
2.1 入队
入队(enqueue)就是把新元素放入队列中,只允许在队尾的位置放入元素,新元素的下一个位置将会成为新的队尾。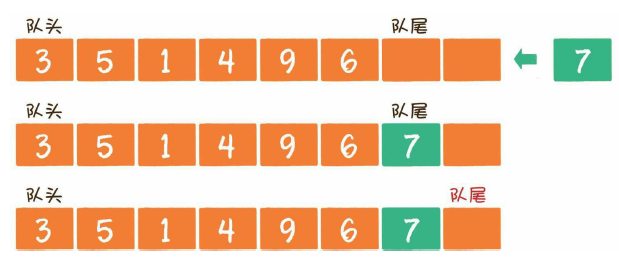
2.2 出队
出队操作(dequeue)就是把元素移出队列,只允许在队头一侧移出元素,出队元素的后一个元素将会成为新的队头。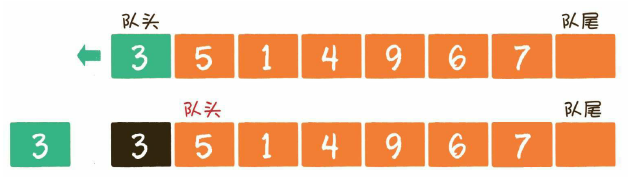
下面我们就来分别实现顺序队列和链式队列
三、队列的设计
3.1 顺序队列
关于顺序队列(底层都是利用数组作为容器)的实现,我们将采用顺序循环队列的结构来实现,在给出实现方案前先来分析一下为什么不直接使用顺序表作为底层容器来实现。
实际上采用顺序表实现队列时,入队操作直接执行顺序表尾部插入操作,其时间复杂度为O(1),出队操作直接执行顺序表头部删除操作,其时间复杂度为O(n),主要用于移动元素,效率低,既然如此,我们就把出队的时间复杂度降为O(1)即可,为此在顺序表中添加一个头指向下标front和尾指向下标,出队和入队时只要改变front、rear的下标指向取值即可,此时无需移动元素,因此出队的时间复杂度也就变为O(1)。其过程如下图所示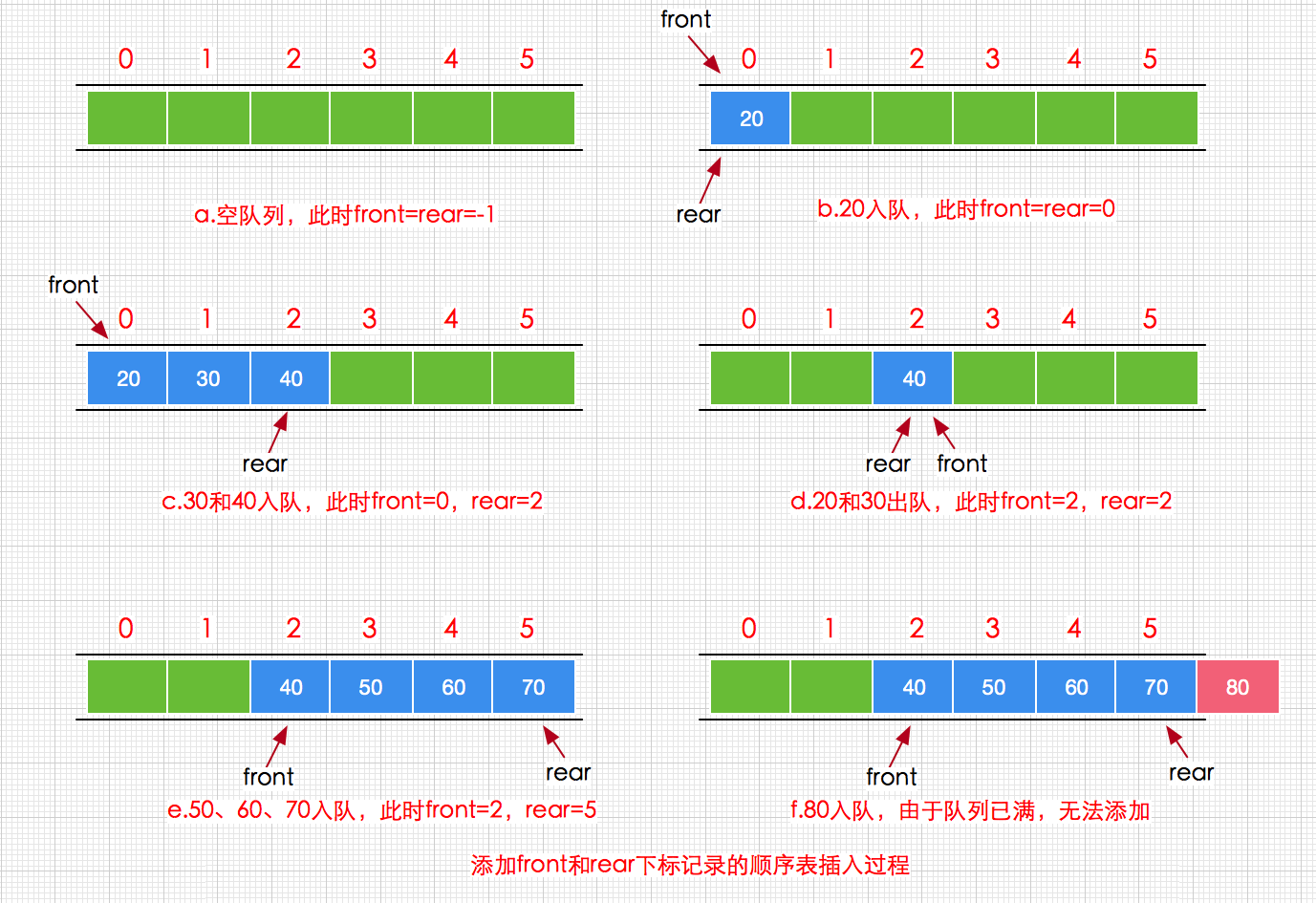
3.2 循环队列
从上节图的演示过程,(a)操作时,是空队列此时front和rear都为-1,同时可以发现虽然我们通过给顺序表添加front和rear变量记录下标后使用得出队操作的时间复杂度降为O(1),但是却出现了另外一个严重的问题,那就是空间浪费,从图中的(d)和(e)操作可以发现,20和30出队后,遗留下来的空间并没有被重新利用,反而是空着,所以导致执行(f)操作时,出现队列已满的假现象,这种假现象我们称之为假溢出,之所以出现这样假溢出的现象是因为顺序表队列的存储单元没有重复利用机制,而解决该问题的最合适的方式就是将顺序队列设计为循环结构,接下来我们就通过循环顺序表来实现队列,可以称为循环队列。
循环队列是什么意思呢?让我们看看下面的例子。
假设一个队列经过反复的入队和出队操作,还剩下2个元素,在“物理”上分布于数组的末尾位置。这时又有一个新元素将要入队。
在数组不做扩容的前提下,如何让新元素入队并确定新的队尾位置呢?我们可以利用已出队元素留下的空间,让队尾指针重新指回数组的首位。
这样一来,整个队列的元素就“循环”起来了。在物理存储上,队尾的位置也可以在队头之前。当再有元素入队时,将其放入数组的首位,队尾指针继续后移即可。
一直到(队尾下标+1)%数组长度 = 队头下标时,代表此队列真的已经满了。需要注意的是,队尾指针指向的位置永远空出1位,所以队列最大容量比数组长度小1。
四、循环队列的实现
循环队列就是将顺序队列设计为在逻辑结构上收尾相接的循环结构,这样我们就可以重复利用存储单元,其整体过程如下图所示:<br />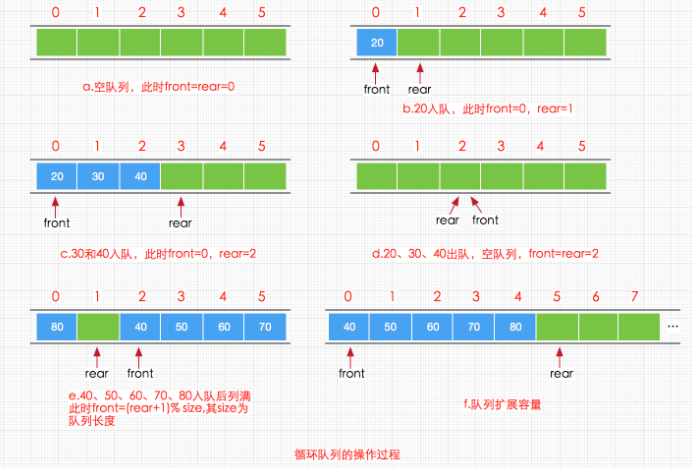<br />简单分析一下:<br />其中采用循环结构的顺序表,可以循环利用存储单元,因此有如下计算关系(其中size为队列长度):
//其中front、rear的下标的取值范围是0~size-1,不会造成假溢出。
front=(front+1)%size;//队头下标
rear=(rear+1)%size;
- front为队头元素的下标,rear则指向下一个入队元素的下标
- 当front=rear时,我们约定队列为空。
- 出队操作改变front下标指向,入队操作改变rear下标指向,size代表队列容量。
- 约定队列满的条件为front=(rear+1)%size,注意此时队列中仍有一个空的位置,此处留一个空位主要用于避免与队列空的条件front=rear相同。
- 队列内部的数组可扩容,并按照原来队列的次序复制元素数组
了解了队列的实现规则后,我们重点分析一下入队add方法和出队poll方法,其中入队add方法实现如下:
/**
* data 入队,添加成功返回true,否则返回false,可扩容
* @param data
* @return
*/
@Override
public boolean add(T data) {
//判断是否满队
if (this.front==(this.rear+1)%this.elementData.length){
ensureCapacity(elementData.length*2+1);
}
//添加data
elementData[this.rear]=data;
//更新rear指向下一个空元素的位置
this.rear=(this.rear+1)%elementData.length;
size++;
return true;
}
在add方法中我们先通过this.front==(this.rear+1)%this.elementData.length判断队列是否满,在前面我们约定过队列满的条件为front=(rear+1)%size,如果队列满,则先通过ensureCapacity(elementData.length*2+1)扩容,该方法实现如下:
/**
* 扩容的方法
* @param capacity
*/
public void ensureCapacity(int capacity) {
//如果需要拓展的容量比现在数组的容量还小,则无需扩容
if (capacity<size)
return;
T[] old = elementData;
elementData= (T[]) new Object[capacity];
int j=0;
//复制元素
for (int i=this.front; i!=this.rear ; i=(i+1)%old.length) {
elementData[j++] = old[i];
}
//恢复front,rear指向
this.front=0;
this.rear=j;
}
这个方法比较简单,主要创建一个新容量的数组,并把旧数组中的元素复制到新的数组中,这里唯一的要注意的是,判断久数组是否复制完成的条件为i!=this.rear,同时循环的自增条件为i=(i+1)%old.length。扩容后直接通过rear添加新元素,最后更新rear指向下一个入队新元素。对于出队操作poll的实现如下:
/**
* 出队,执行删除操作,返回队头元素,若队列为空,返回null
* @return
*/
@Override
public T poll() {
T temp=this.elementData[this.front];
this.front=(this.front+1)%this.elementData.length;
size--;
return temp;
}
出队操作相对简单些,直接存储要删除元素的数据,并更新队头front的值,最后返回删除元素的数据。ok~,关于循环结构的顺序队列,我们就分析到此,最后给出循环顺序队列的实现源码,其他方法比较简单,注释也很清楚,就不过多分析了:
/**
* 循环队列的实现
*/
public class SeqQueue<T> {
private T elementData[]; //存放元素的数组
private int front,rear; //队头、队尾指针
private int size;
public SeqQueue(){
elementData= (T[]) new Object[10];
front=rear=0;
}
public SeqQueue(int capacity){
elementData= (T[]) new Object[capacity];
front=rear=0;
}
//获取队列的长度
public int size() {
return size;
}
//判断队列是否为空
public boolean isEmpty() {
return front==rear;
}
//入队,可扩容
public boolean add(T data) {
//判断是否满队(满队条件为front=(rear+1)%size,因为队头、队尾至少间隔一个空间)
if (front==(rear+1)%elementData.length){
ensureCapacity(elementData.length*2+1);
}
//添加data
elementData[rear]=data;
//更新rear指向下一个空元素的位置
rear=(rear+1)%elementData.length;
size++;
return true;
}
//返回队头元素,不执行删除操作,若队列为空,返回null
public T peek() {
return elementData[front];
}
//出队,执行删除操作,返回队头元素,若队列为空,返回null
public T poll() {
T temp=this.elementData[this.front];
this.front=(this.front+1)%this.elementData.length;
size--;
return temp;
}
//扩容的方法
public void ensureCapacity(int capacity) {
//如果需要拓展的容量比现在数组的容量还小,则无需扩容
if (capacity<size)
return;
T[] old = elementData;
elementData= (T[]) new Object[capacity];
int j=0;
//复制元素
for (int i=this.front; i!=this.rear ; i=(i+1)%old.length) {
elementData[j++] = old[i];
}
//恢复front,rear指向
this.front=0;
this.rear=j;
}
public static void main(String[] args) {
SeqQueue<String> sq = new SeqQueue<>();
sq.add("A");
sq.add("B");
sq.add("C");
System.out.println("size->"+sq.size());
int l=sq.size(); //size 在减少,必须先记录
for (int i=0;i<l;i++){
System.out.println("sq.poll->"+sq.poll());
}
sq.add("D");
System.out.println("sq.peek->"+sq.peek());
}
}
五、链式队列的实现
分析完顺序队列,我们接着看看链式队列的设计与实现,对于链式队列,将使用带头指针front和尾指针rear的单链表实现,front直接指向队头的第一个元素,rear指向队尾的最后一个元素,其结构如下: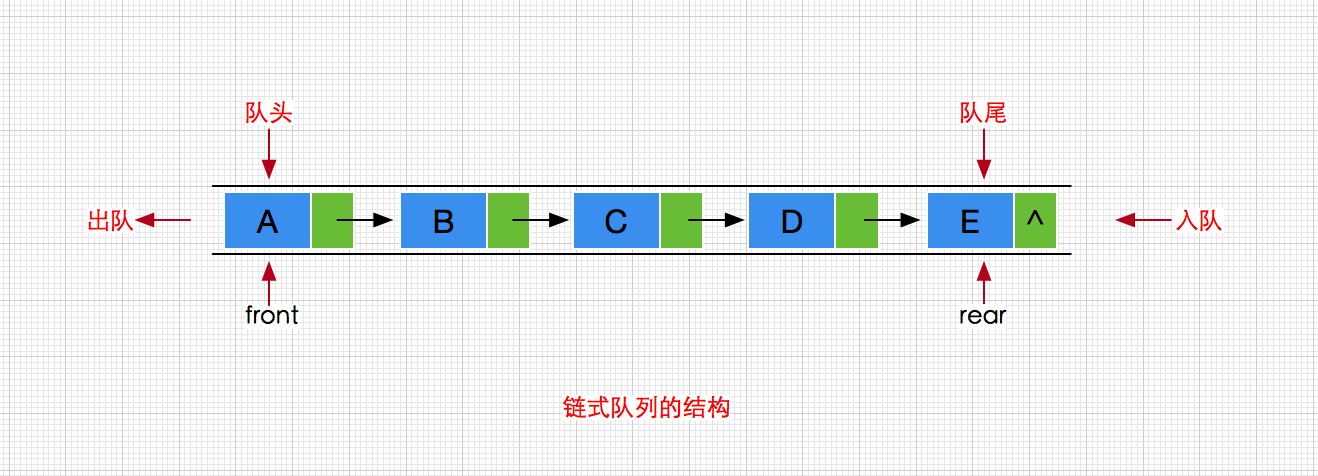
之所以选择单链表(带头尾指针)而不采用循环双链表或者双链表主要是双链表的空间开销(空间复杂度,多前继指针)相对单链表来说大了不少,而单链表只要新增头指针和尾指针就可以轻松实现常数时间内(时间复杂度为O(1))访问头尾结点。下面我们来看看如何设计链式队列:
- 以上述的图为例分别设置front和rear指向队头结点和队尾结点,使用单链表的头尾访问时间复杂度为O(1)。
- 设置初始化空队列,使用front=rear=null,并且约定条件
front==null&&rear==null成立时,队列为空。 - 出队操作时,若队列不为空获取队头结点元素,并删除队头结点元素,更新front指针的指向为front=front.next
- 入队操作时,使插入元素的结点在rear之后并更新rear指针指向新插入元素。
- 当第一个元素入队或者最后一个元素出队时,同时更新front指针和rear指针的指向。
这一系列过程如下图所示:
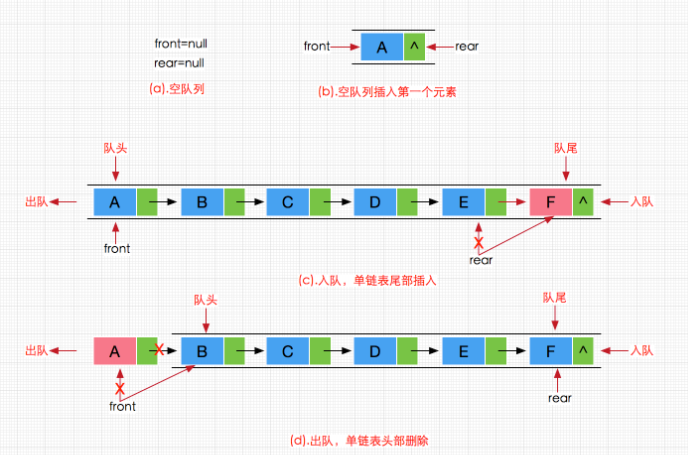
ok~,关于链式队列的设计都分析完,至于实现就比较简单了,和之前分析过的单链表区别不大,因此这里我们直接给出实现代码即可:
/**
* 链式队列的实现
*/
public class LinkedQueue<T> {
// 链表节点
private static class Node<T> {
T data;
Node next;
Node(T data, Node next) {
this.data = data;
this.next = next;
}
}
//指向队头和队尾的结点 front==null&&rear==null时,队列为空
private Node<T> front, rear;
private int size;
//返回队列长度
public int size() {
return size;
}
//判断队列是否为空
/**
* 这里的判断队列是否为空与循环链表不同,
* 由于存在头指针与尾指针指向同一个元素的情况,
* 所以当front==null&&rear==null时,队列为空
*/
public boolean isEmpty() {
return front == null && rear == null;
}
//入队
public boolean add(T data) {
Node<T> q = new Node<>(data, null);
if (this.front == null) {// 空队列插入
this.front = q;
} else {// 非空队列,尾部插入
this.rear.next = q;
}
this.rear = q;
size++;
return true;
}
//返回队头元素,不执行删除操作,若队列为空,返回null
public T peek() {
return this.isEmpty() ? null : this.front.data;
}
//出队,执行删除操作,返回队头元素,若队列为空,返回null
public T poll() {
if (this.isEmpty())
return null;
T x = this.front.data;
this.front = this.front.next;
if (this.front == null)
this.rear = null;
size--;
return x;
}
public static void main(String[] args) {
LinkedQueue<String> q = new LinkedQueue<>();
q.add("A");
q.add("B");
q.add("C");
System.out.println("size->"+q.size());
int l=q.size(); //size 在减少,必须先记录
for (int i=0;i<l;i++){
System.out.println("q.poll->"+q.poll());
}
q.add("D");
System.out.println("q.peek->"+q.peek());
}
}

