后序遍历（LRD）是 二叉树遍历的一种，也叫做 后根遍历、后序周游，可记做左右根。后序遍历有 递归算法和非递归算法两种。在二叉树中，先左后右再根。巧记：左右根。
后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。即：
若 二叉树为空则结束返回，
否则：
（1）后序遍历左子树
（2）后序遍历右子树
（3）访问根结点
如图所示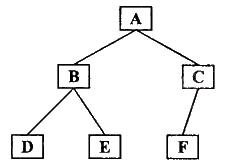

后序遍历结果：DEBFCA

实现代码

public class Test {
    public static void main(String[] args) {
        // 以数组形式生成一棵完全二叉树
        TreeNode[] node = new TreeNode[10];
        for (int i = 0; i < 10; i++) {
            node[i] = new TreeNode(i);
        }
        for (int i = 0; i < 10; i++) {
            if (i * 2 + 1 < 10)
                node[i].left = node[i * 2 + 1];
            if (i * 2 + 2 < 10)
                node[i].right = node[i * 2 + 2];
        }
        postOrderRe(node[0]);
    }
    public static void postOrderRe(TreeNode biTree) {
        // 后序遍历递归实现
        if (biTree == null) {
            return;
        } else {
            postOrderRe(biTree.left);
            postOrderRe(biTree.right);
            System.out.print(biTree.value + " ");
        }
    }
}
//节点结构
class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    TreeNode(int value) {
        this.value = value;
    }
}