后序遍历（LRD）是 二叉树遍历的一种，也叫做 后根遍历、后序周游，可记做左右根。后序遍历有 递归算法和非递归算法两种。在二叉树中，先左后右再根。巧记：左右根。
后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。即：
若 二叉树为空则结束返回，否则：
（1）后序遍历左子树
（2）后序遍历右子树
（3）访问根结点
如图所示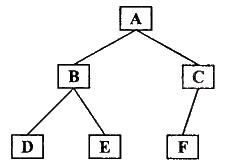

后序遍历结果：DEBFCA

算法核心思想：

首先要搞清楚先序、中序、后序的非递归算法共同之处：用栈来保存先前走过的路径，以便可以在访问完子树后,可以利用栈中的信息,回退到当前节点的双亲节点,进行下一步操作。<br />    后序遍历的非递归算法是三种顺序中最复杂的，原因在于，后序遍历是先访问左、右子树,再访问根节点，而在非递归算法中，利用栈回退到时，并不知道是从左子树回退到根节点，还是从右子树回退到根节点，如果从左子树回退到根节点，此时就应该去访问右子树，而如果从右子树回退到根节点，此时就应该访问根节点。所以相比前序和后序，必须得在压栈时添加信息，以便在退栈时可以知道是从左子树返回，还是从右子树返回进而决定下一步的操作。

实现代码

import java.util.Stack;

public class Test {
    public static void main(String[] args) {
        TreeNode[] node = new TreeNode[10];// 以数组形式生成一棵完全二叉树
        for (int i = 0; i < 10; i++) {
            node[i] = new TreeNode(i);
        }
        for (int i = 0; i < 10; i++) {
            if (i * 2 + 1 < 10)
                node[i].left = node[i * 2 + 1];
            if (i * 2 + 2 < 10)
                node[i].right = node[i * 2 + 2];
        }
        // 后序遍历非递归实现
        postOrderRe(node[0]);
    }

    public static void postOrderRe(TreeNode biTree) {
        int leftFlag = 1;// 在辅助栈里表示左节点
        int rightFlag = 2;// 在辅助栈里表示右节点
        Stack<TreeNode> stack = new Stack<TreeNode>();
        // 辅助栈，用来判断子节点返回父节点时处于左节点还是右节点。
        Stack<Integer> stackHelp = new Stack<Integer>();
        while (biTree != null || !stack.empty()) {
            while (biTree != null) {
                // 将节点压入栈1，并在栈2将节点标记为左节点
                stack.push(biTree);
                stackHelp.push(leftFlag);
                biTree = biTree.left;
            }
            while (!stack.empty() && stackHelp.peek() == rightFlag) {
                // 如果是从右子节点返回父节点，则任务完成，将两个栈的栈顶弹出
                stackHelp.pop();
                System.out.print(stack.pop().value + " ");
            }
            if (!stack.empty() && stackHelp.peek() == leftFlag) {
                // 如果是从左子节点返回父节点，则将标记改为右子节点
                stackHelp.pop();
                stackHelp.push(rightFlag);
                biTree = stack.peek().right;
            }
        }
    }
}

//节点结构
class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;

    TreeNode(int value) {
        this.value = value;
    }
}