一、栈的概述:
要弄明白什么是栈,我们需要先举一个生活中的例子。<br /> <br /> 假如有一个又细又长的圆筒,圆筒一端封闭,另一端开口。往圆筒里放入乒乓球,先放入的靠近圆筒底部,后放入的靠近圆筒入口。<br /><br /> 那么,要想取出这些乒乓球,则只能按照和放入顺序相反的顺序来取,先取出后放入的,再取出先放入的,而不可能把最里面最先放入的乒乓球优先取出。<br />
栈(stack)是一种线性数据结构,它就像一个上图所示的放入乒乓球的圆筒容器,栈中的元素只能先入后出(First In Last Out,简称FILO)。最早进入的元素存放的位置叫作栈底(bottom),最后进入的元素存放的位置叫作栈顶(top)。
栈这种数据结构既可以用数组来实现,也可以用链表来实现。
二、栈的功能说明
栈是一种用于存储数据的简单数据结构,有点类似链表或者顺序表(统称线性表),栈与线性表的最大区别是数据的存取的操作,我们可以这样认为栈(Stack)是一种特殊的线性表,其插入和删除操作只允许在线性表的一端进行,一般而言,把允许操作的一端称为栈顶(Top),不可操作的一端称为栈底(Bottom),同时把插入元素的操作称为入栈(Push),删除元素的操作称为出栈(Pop)。若栈中没有任何元素,则称为空栈,栈的结构如下图: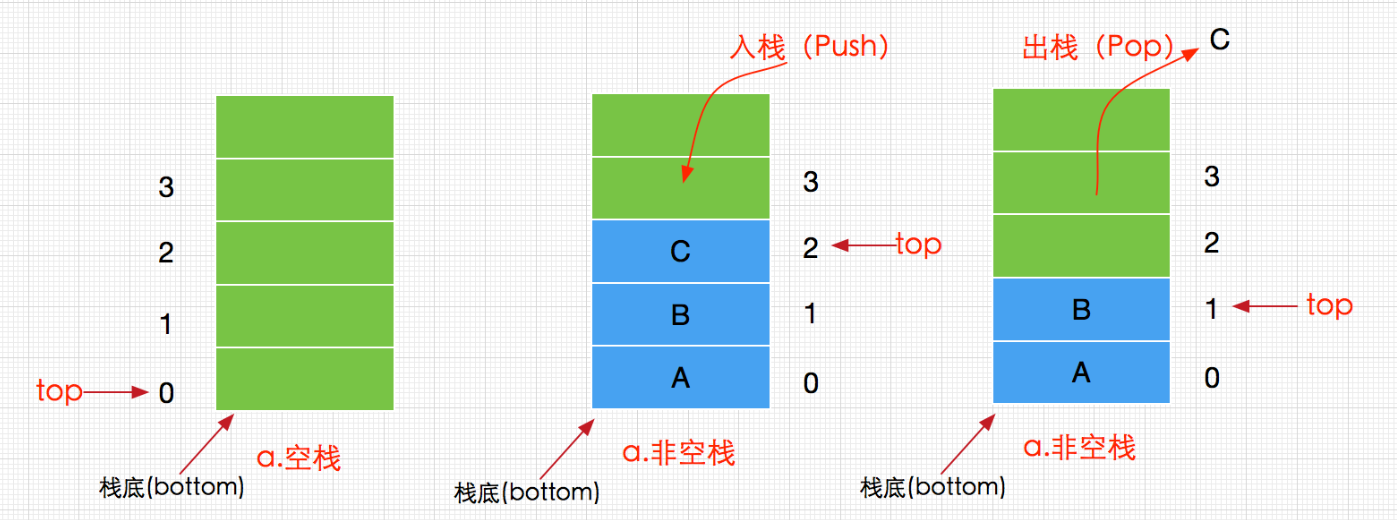
由图我们可看成栈只能从栈顶存取元素,同时先进入的元素反而是后出,而栈顶永远指向栈内最顶部的元素。到此可以给出栈的正式定义:
栈(Stack)是一种有序特殊的线性表,只能在表的一端(称为栈顶,top,总是指向栈顶元素)执行插入和删除操作,最后插入的元素将第一个被删除,因此栈也称为后进先出(Last In First Out,LIFO)或先进后出(First In Last Out FILO)的线性表。
栈的基本操作创建栈,判空,入栈,出栈,获取栈顶元素等,注意栈不支持对指定位置进行删除,插入;一般定义方法如下:
| 方法 | 功能 |
|---|---|
| push() | 元素入栈 |
| pop() | 出栈,返回栈顶元素,同时从栈中移除该元素 |
| peek() | 返回栈顶元素,未出栈 |
| isEmpty() | 栈是否为空 |
完成接口Stack声明,代码如下:
/**
* 栈接口抽象数据类型
*/
public interface Stack<T> {
/**
* 栈是否为空
* @return
*/
boolean isEmpty();
/**
* data元素入栈
* @param data
*/
void push(T data);
/**
* 出栈,返回栈顶元素,同时从栈中移除该元素
* @return
*/
T pop();
/**
* 返回栈顶元素,未出栈
* @return
*/
T peek();
}
2.1 入栈
入栈操作(push)就是把新元素放入栈中,只允许从栈顶一侧放入元素,新元素的位置将会成为新的栈顶。<br />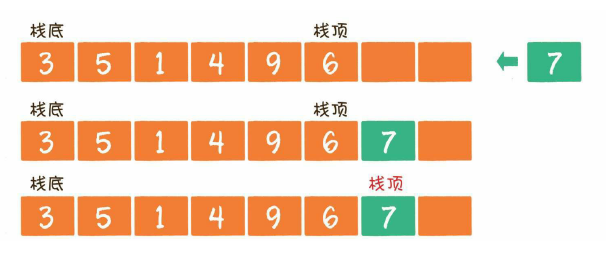
2.2 出栈
出栈操作(pop)就是把元素从栈中弹出,只有栈顶元素才允许出栈,出栈元素的前一个元素将会成为新的栈顶。<br />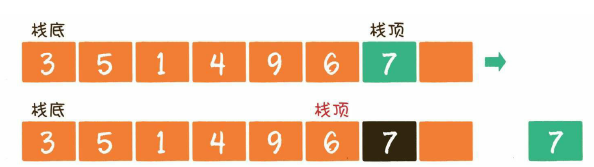
三、使用数组实现栈
栈的内部以数组或顺序表为基础,实现对元素的存取操作,也可以称为顺序栈。
我们使用内部数据组来实现栈。这里先声明一个顺序栈其代码如下,实现Stack和Serializable接口:
/**
* 顺序栈的实现
*/
public class SeqStack<T> implements Stack<T>,Serializable {
private static final long serialVersionUID = -5413303117698554397L;
/**
* 栈顶指针,-1代表空栈
*/
private int top=-1;
/**
* 容量大小默认为10
*/
private int capacity=10;
/**
* 存放元素的数组
*/
private T[] array;
private int size;
public SeqStack(int capacity){
array = (T[]) new Object[capacity];
}
public SeqStack(){
array= (T[]) new Object[this.capacity];
}
//.......省略其他代码
}
其获取栈顶元素值的peek操作过程如下图(未删除只获取值):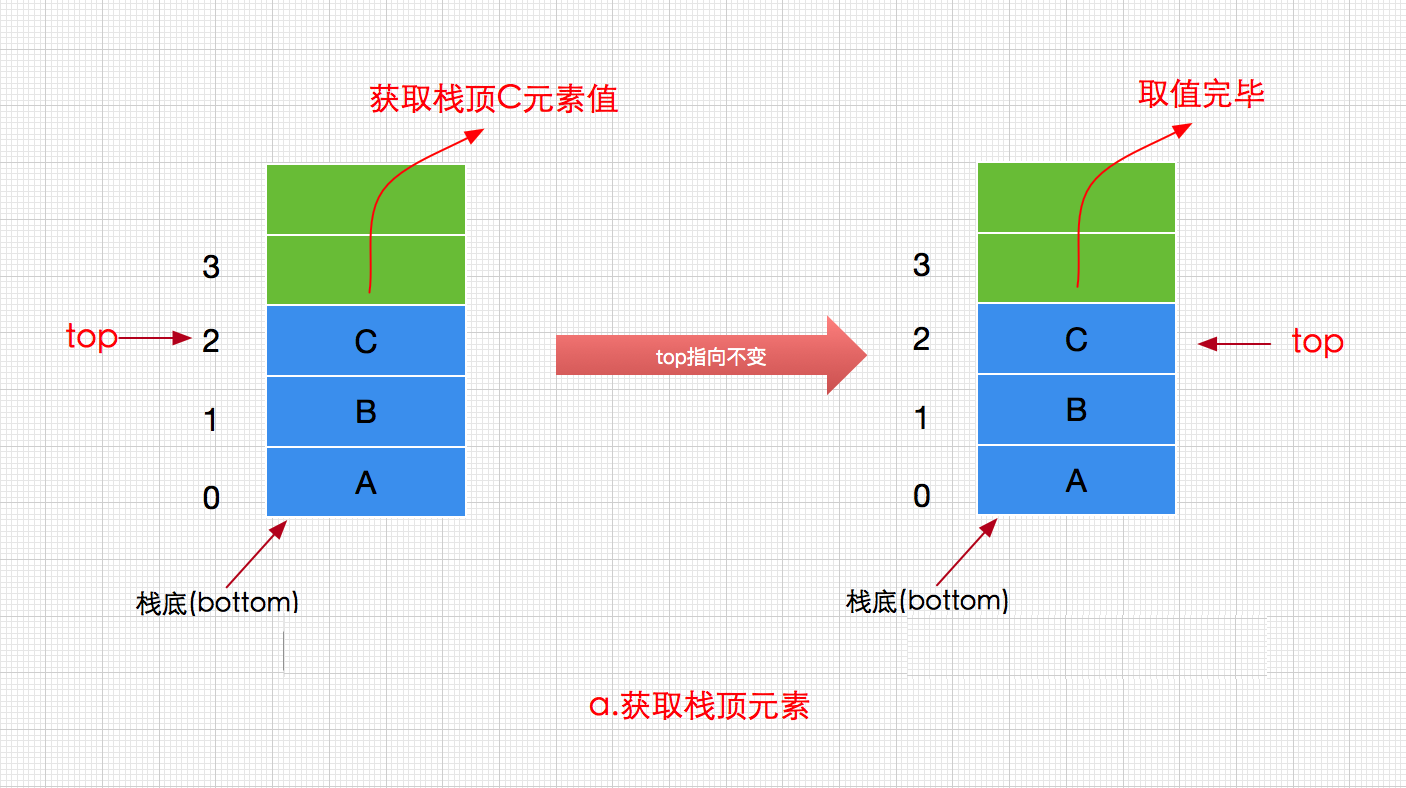
代码如下:
/**
* 获取栈顶元素的值,不删除
* @return
*/
@Override
public T peek() {
if(isEmpty())
new EmptyStackException();
return array[top];
}
从栈添加元素的过程如下(更新栈顶top指向):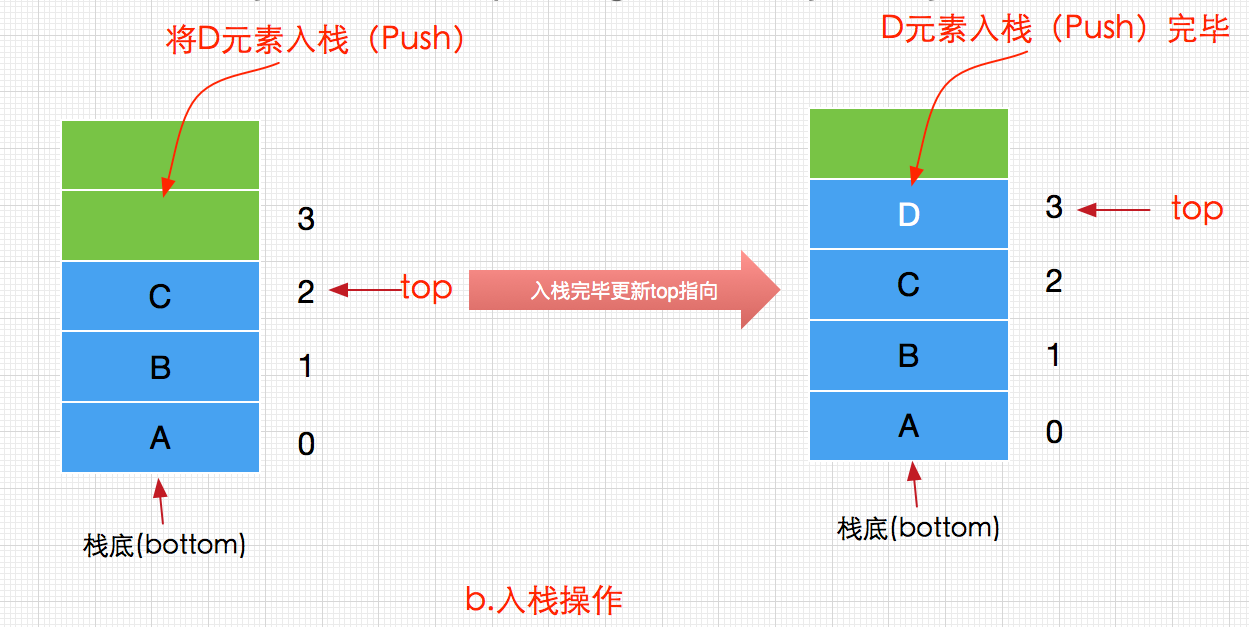
代码如下:
/**
* 添加元素,从栈顶(数组尾部)插入
* 容量不足时,需要扩容
* @param data
*/
@Override
public void push(T data) {
//判断容量是否充足
if(array.length==size)
ensureCapacity(size*2+1);//扩容
//从栈顶添加元素
array[++top]=data;
size++;
}
栈弹出栈顶元素的过程如下(删除并获取值):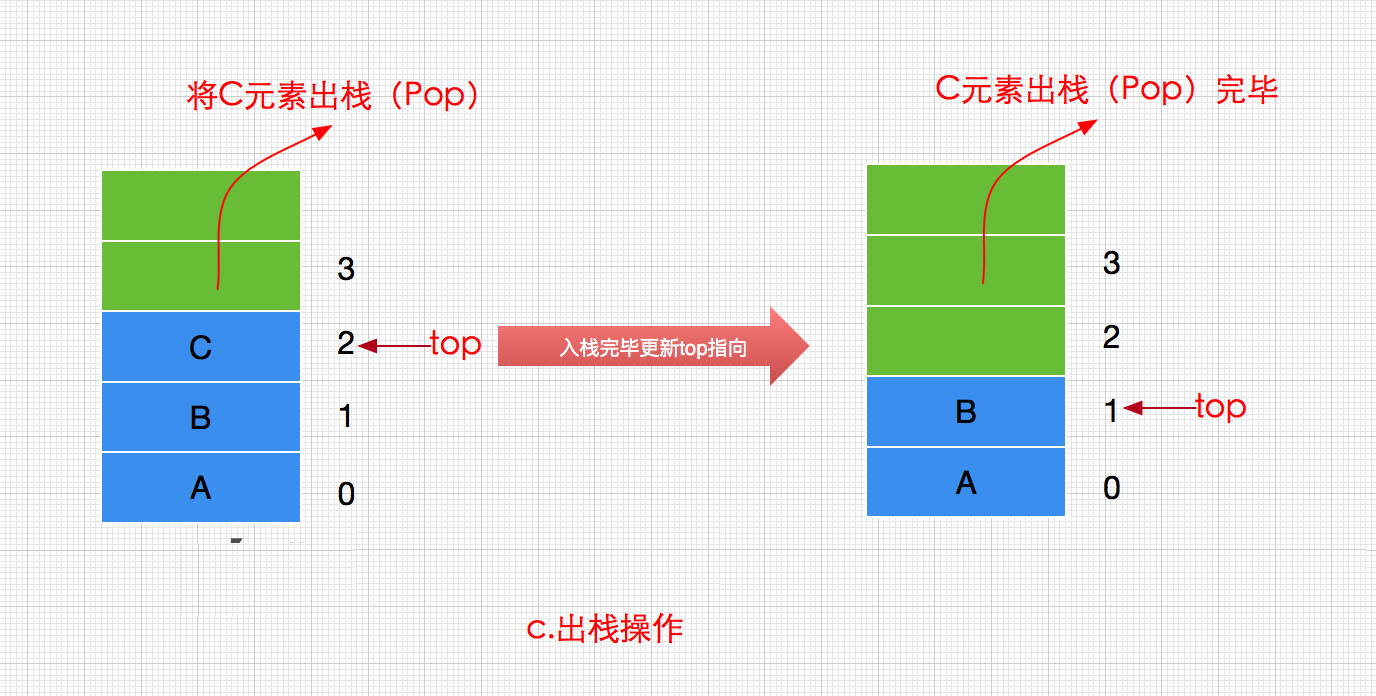
代码如下:
/**
* 从栈顶(顺序表尾部)删除
* @return
*/
@Override
public T pop() {
if(isEmpty())
new EmptyStackException();
size--;
return array[top--];
}
到此,顺序栈的主要操作已实现完,是不是发现很简单,确实如此,栈的主要操作就这样,当然我们也可以通过前一篇介绍的MyArrayList作为基础来实现顺序栈,这个也比较简单,后面也会提供带代码,这里就不过多啰嗦了。下面给出顺序栈的整体实现代码:
import java.util.EmptyStackException;
/**
* 顺序栈的实现
*/
public class SeqStack<T> {
/**
* 栈顶指针,-1代表空栈
*/
private int top=-1;
/**
* 容量大小默认为10
*/
private int capacity=10;
/**
* 存放元素的数组
*/
private T[] array;
private int size;
public SeqStack(int capacity){
array = (T[]) new Object[capacity];
}
public SeqStack(){
array= (T[]) new Object[this.capacity];
}
public int size(){
return size;
}
@Override
public boolean isEmpty() {
return this.top==-1;
}
/**
* 添加元素,从栈顶(数组尾部)插入
* @param data
*/
@Override
public void push(T data) {
//判断容量是否充足
if(array.length==size)
ensureCapacity(size*2+1);//扩容
//从栈顶添加元素
array[++top]=data;
size++;
}
/**
* 获取栈顶元素的值,不删除
* @return
*/
@Override
public T peek() {
if(isEmpty())
new EmptyStackException();
return array[top];
}
/**
* 从栈顶(顺序表尾部)删除
* @return
*/
@Override
public T pop() {
if(isEmpty())
new EmptyStackException();
size--;
return array[top--];
}
/**
* 扩容的方法
* @param capacity
*/
public void ensureCapacity(int capacity) {
//如果需要拓展的容量比现在数组的容量还小,则无需扩容
if (capacity<size)
return;
T[] old = array;
array = (T[]) new Object[capacity];
//复制元素
for (int i=0; i<size ; i++)
array[i]=old[i];
}
public static void main(String[] args){
SeqStack<String> s=new SeqStack<>();
s.push("A");
s.push("B");
s.push("C");
System.out.println("size->"+s.size());
int l=s.size();//size 在减少,必须先记录
for (int i=0;i<l;i++){
System.out.println("s.pop->"+s.pop());
}
System.out.println("s.peek->"+s.peek());
}
}
四、使用链表实现栈
了解完顺序栈,我们接着来看看链式栈,所谓的链式栈(Linked Stack),就是采用链式存储结构的栈,由于我们操作的是栈顶一端,因此这里采用单链表(不带头结点)作为基础,直接实现栈的添加,获取,删除等主要操作即可。其操作过程如下图: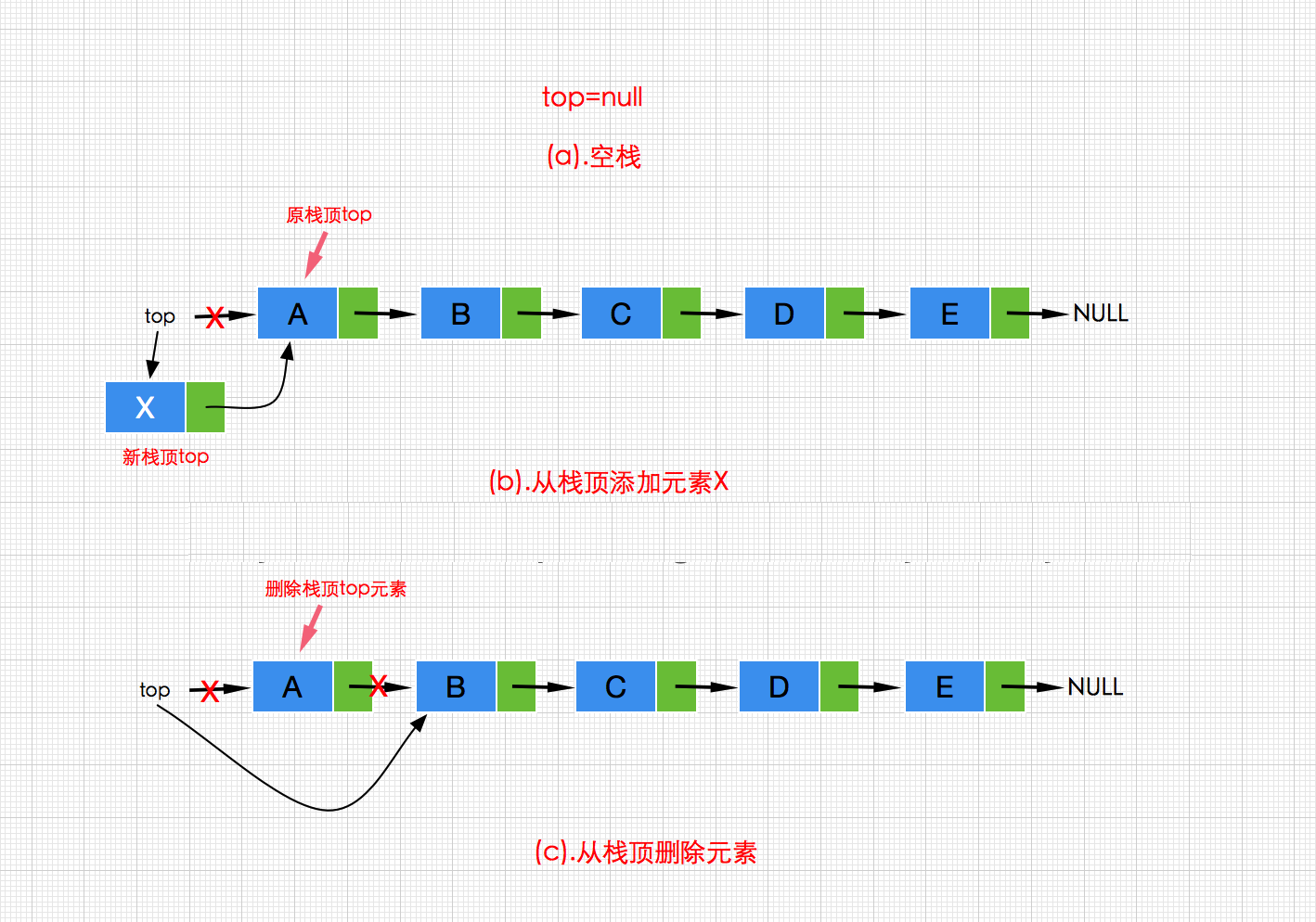
从图可以看出,无论是插入还是删除直接操作的是链表头部也就是栈顶元素,因此我们只需要使用不带头结点的单链表即可。代码实现如下,比较简单,不过多分析了:
/**
* 栈的链式实现
*/
public class LinkedStack<T> {
// 链表节点
private static class Node<T> {
T data;
Node next;
Node(T data,Node next) {
this.data = data;
this.next = next;
}
}
private Node<T> top; //栈顶指针
private int size; //栈的长度
//获取栈的长度
public int size() {
return size;
}
//判断栈是否为空
public boolean isEmpty() {
return top == null || top.data == null;
}
//入栈
public void push(T data){
if (this.top == null) {// 调用pop()后top可能为null
this.top = new Node<>(data, null);
} else if (this.top.data == null) {
this.top.data = data;
} else {
Node<T> p = new Node<>(data, this.top);
top = p;// 更新栈顶
}
size++;
}
//获取栈顶元素
public T peek(){
if (isEmpty()) {
throw new EmptyStackException();
}
return top.data;
}
//出栈
public T pop(){
if (isEmpty()) {
throw new EmptyStackException();
}
T data = top.data;
top = top.next;
size--;
return data;
}
public static void main(String[] args) {
LinkedStack<String> sl = new LinkedStack<>();
sl.push("A");
sl.push("B");
sl.push("C");
int length = sl.size();
for (int i = 0; i < length; i++) {
System.out.println("sl.pop->" + sl.pop());
}
}
}
最后我们来看看顺序栈与链式栈中各个操作的算法复杂度(时间和空间)对比,顺序栈复杂度如下:
| 操作 | 时间复杂度 |
|---|---|
| SeqStack空间复杂度(用于N次push) | O(n) |
| push()时间复杂度 | O(1) |
| pop()时间复杂度 | O(1) |
| peek()时间复杂度 | O(1) |
| isEmpty()时间复杂度 | O(1) |
链式栈复杂度如下:
| 操作 | 时间复杂度 |
|---|---|
| SeqStack空间复杂度创建(用于N次push) | O(n) |
| push()时间复杂度 | O(1) |
| pop()时间复杂度 | O(1) |
| peek()时间复杂度 | O(1) |
| isEmpty()时间复杂度 | O(1) |
由此可知栈的主要操作都可以在常数时间内完成,这主要是因为栈只对一端进行操作,而且操作的只是栈顶元素。
五、栈的应用
栈是一种很重要的数据结构,在计算机中有着很广泛的应用,如下一些操作都应用到了栈。
- 符号匹配
- 中缀表达式转换为后缀表达式
- 计算后缀表达式
- 实现函数的嵌套调用
- HTML和XML文件中的标签匹配
- 网页浏览器中已访问页面的历史记录
接下来我们分别对符合匹配,中缀表达式转换为后缀表达式进行简单的分析,以加深我们对栈的理解。
- 符号匹配在编写程序的过程中,我们经常会遇到诸如圆括号“()”与花括号“{}”,这些符号都必须是左右匹配的,这就是我们所说的符合匹配类型,当然符合不仅需要个数相等,而且需要先左后右的依次出现,否则就不符合匹配规则,如“)(”,明显是错误的匹配,而“()”才是正确的匹配。有时候符合如括号还会嵌套出现,如“9-(5+(5+1))”,而嵌套的匹配原则是一个右括号与其前面最近的一个括号匹配,事实上编译器帮我检查语法错误是也是执行一样的匹配原理,而这一系列操作都需要借助栈来完成,接下来我们使用栈来实现括号”()”是否匹配的检测。判断原则如下(str=”((5-3)*8-2)”):
- a.设置str是一个表达式字符串,从左到右依次对字符串str中的每个字符char进行语法检测,如果char是,左括号则入栈,如果char是右括号则出栈(有一对匹配就可以去匹配一个左括号,因此可以出栈),若此时出栈的字符char为左括号,则说明这一对括号匹配正常,如果此时栈为空或者出栈字符不为左括号,则表示缺少与char匹配的左括号,即目前不完整。
- b.重复执行a操作,直到str检测结束,如果此时栈为空,则全部括号匹配,如果栈中还有左括号,是说明缺少右括号。
- 整个检测算法的执行流程如下图 :
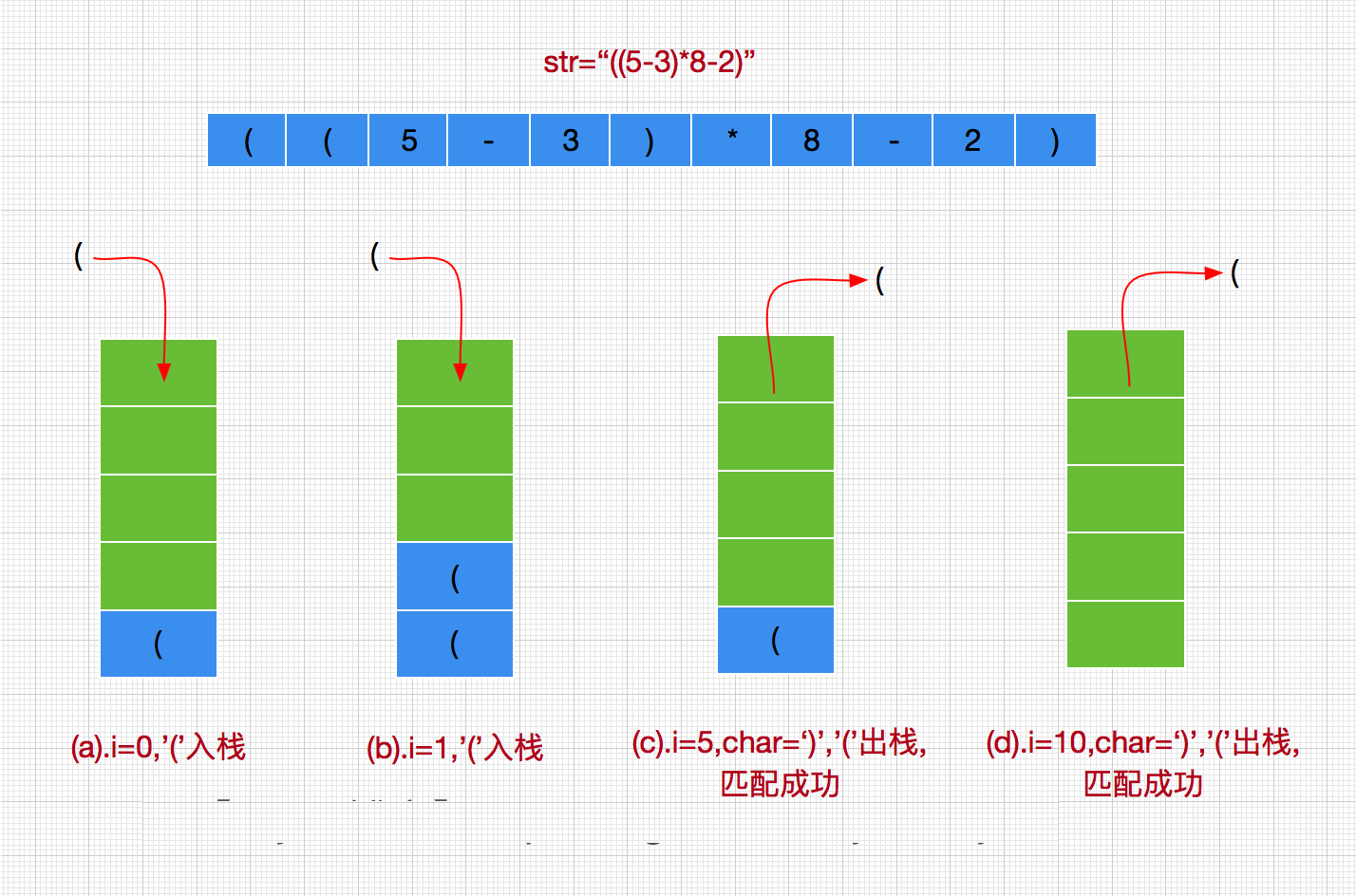
接着我们用栈作为存储容器通过代码来实现这个过程,代码如下: ```java /**
- 表达式检测 */ import java.util.Stack;
public class CheckExpression {
public static boolean isValid(String expstr) {
// 创建栈
Stack<Character> stack = new Stack<>();
// 遍历字符串中的每一个字符
for (int i = 0; i < expstr.length(); i++) {
char ch = expstr.charAt(i);
// 如果当前字符是左括号就直接入栈
if (ch == '(') {
stack.push(ch);
} else if (ch == ')') {
// 栈中只有左括号,所以当前字符为')'时栈空了,就相当于栈中没有对应的'('了
if (stack.isEmpty()) {
return false;
}
// 如果当前字符是右括号就出栈
stack.pop();
}
}
return stack.isEmpty();
}
public static void main(String args[]) {
String expstr = "((5-3)*8-2)";
System.out.println(isValid(expstr));
}
} ```

