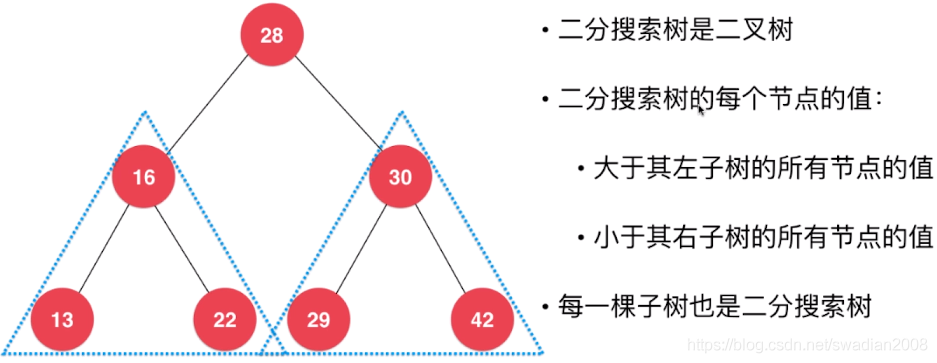
1、二分搜索树(BST:Binary Search Tree)说明
二分搜索树(BST:Binary Search Tree)或者称为二叉查找树是一种特殊的二叉树,它改善了二叉树节点查找的效率。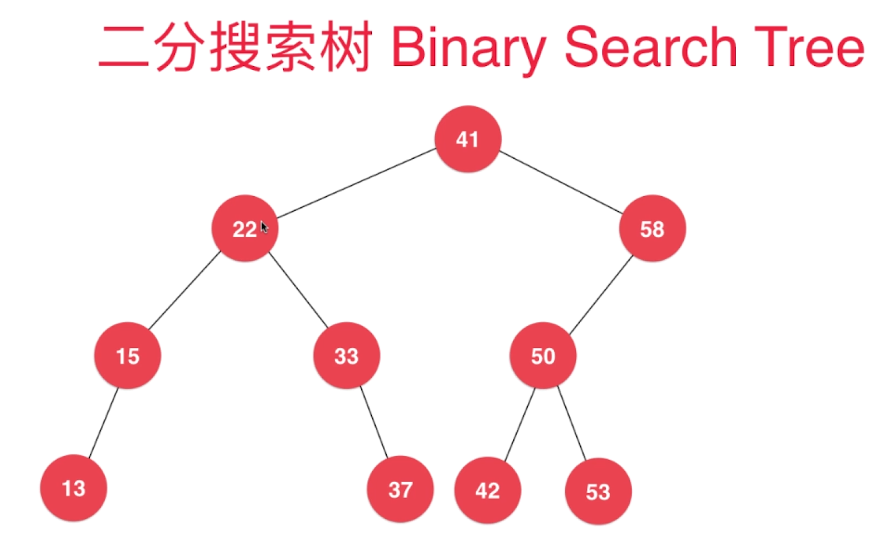
2、二分搜索树性质:
需要满足以下两个条件:
- 本身是有序树(若将树中每个结点的各子树看成是从左到右有次序的(即不能互换),则称该树为有序树(Ordered Tree));
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
对于任意一个节点 n
- 其左子树(left subtree)下的每个后代节点(descendant node)的值都小于节点 n 的值;
- 其右子树(right subtree)下的每个后代节点的值都大于节点 n 的值。
所谓节点 n 的子树,可以将其看作是以节点 n 为根节点的树。子树的所有节点都是节点 n 的后代,而子树的根则是节点 n 本身。
二分搜索树可以非常大的提高我们查找数据的速度。比如我们需要查找42这个数据,就可以直接去根节点28的右子树查找,这是因为根据二分搜索树的定义,根节点的左子树此时的数据都是小于28的。
正因为二分搜索树的这个特点,所以,要求使用二分搜索树进行存储的数据都必须具备可比较性。
举例:
下图中展示了两个二叉树。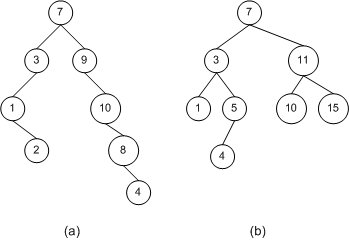
(a)不是二分搜索树。因为节点 10 的右孩子节点 8 小于节点 10,但却出现在节点 10 的右子树中。同样,节点 8 的右孩子节点 4 小于节点 8,但出现在了它的右子树中。
(b)是一个二分搜索树(BST),它符合二叉查找树的性质规定。
无论是在哪个位置,只要不符合二叉查找树的性质规定,就不是二叉查找树。例如,节点 9 的左子树只能包含值小于节点 9 的节点,也就是 8 和 4。
构建二分搜索树代码
1、创建节点类
public class Node<E> {public E e;public Node left;public Node right;public Node(E e) {this.e = e;this.left = null;this.right = null;}public Node() {this(null);}}
2、创建二分搜索树
为了让大家对二分搜索树有一个直观的认识,我们创建二分搜索树如下。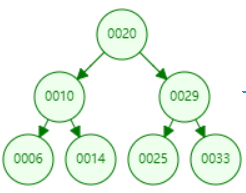
代码
public class TestMain {
public static void main(String[] args) {
int[] arr = {6,10,14,20,25,29,33};
Node<Integer>[] nodeArr = new Node[arr.length];
for (int i=0;i<arr.length;i++) {
nodeArr[i] = new Node<Integer>(arr[i]);
}
nodeArr[3].left = nodeArr[1];
nodeArr[3].right = nodeArr[5];
nodeArr[1].left = nodeArr[0];
nodeArr[1].right = nodeArr[2];
nodeArr[5].left = nodeArr[4];
nodeArr[5].right = nodeArr[6];
}
}
3、二分查找说明:
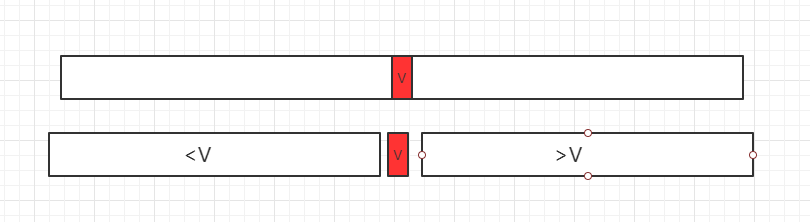
从二分搜索树的性质可知,BST 各节点存储的数据必须能够与其他的节点进行比较。给定任意两个节点,BST 必须能够判断这两个节点的值是小于、大于还是等于。<br /> 二分查找法的思想在 1946 年提出,查找问题是计算机中非常重要的基础问题,对于有序数列,才能使用二分查找法。如果我们要查找一元素,先看数组中间的值V和所需查找数据的大小关系,分三种情况:
- 等于所要查找的数据V,直接找到
- 小于所要查找的数据 V,在小于 V 部分分组继续查询
- 大于所要查找的数据 V,在大于 V 部分分组继续查询
假设我们要查找 BST 中的某一个节点。例如在上图中的二分搜索树(b)中,我们要查找值为 10 的节点。<br /> 我们从根开始查找。可以看到,根节点的值为 7,小于我们要查找的节点值 10。因此,如果节点 10 存在,必然存在于其右子树中,所以应该跳到节点 11 继续查找。此时,节点值 10 小于节点 11 的值,则节点 10 必然存在于节点 11 的左子树中。在查找节点 11 的左孩子,此时我们已经找到了目标节点 10,定位于此。<br /> 如果我们要查找的节点在树中不存在呢?例如,我们要查找节点 9。重复上述操作,直到到达节点 10,它大于节点 9,那么如果节点 9 存在,必然存在于节点 10 的左子树中。然而我们看到节点 10 根本就没有左孩子,因此节点 9 在树中不存在。<br />总结来说,我们使用的查找算法过程如下:<br /> 假设我们要查找节点 n,从 BST 的根节点开始。算法不断地比较节点值的大小直到找到该节点,或者判定不存在。每一步我们都要处理两个节点:树中的一个节点,称为节点 c,和要查找的节点 n,然后并比较 c 和 n 的值。开始时,节点 c 为 BST 的根节点。然后执行以下步骤:
- 如果 c 值为空,则 n 不在 BST 中;
- 比较 c 和 n 的值;
- 如果值相同,则找到了指定节点 n;
- 如果 n 的值小于 c,那么如果 n 存在,必然在 c 的左子树中。回到第 1 步,将 c 的左孩子作为 c;
如果 n 的值大于 c,那么如果 n 存在,必然在 c 的右子树中。回到第 1 步,将 c 的右孩子作为 c;
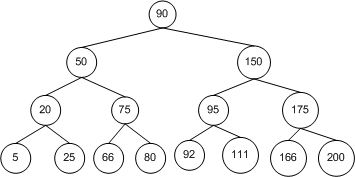
通过 BST 查找节点,理想情况下我们需要检查的节点数可以减半。如下图中的 BST 树,包含了 15 个节点。从根节点开始执行查找算法,第一次比较决定我们是移向左子树还是右子树。对于任意一种情况,一旦执行这一步,我们需要访问的节点数就减少了一半,从 15 降到了 7。同样,下一步访问的节点也减少了一半,从 7 降到了 3,以此类推。
根据这一特点,查找算法的时间复杂度应该是 O(log2n),简写为 O(lg n)。我们分析时间复杂度。可知,log2n = y,相当于 2y = n。即,如果节点数量增加 n,查找时间只缓慢地增加到 log2n。下图中显示了 O(log2n) 和线性增长 O(n) 的增长率之间的区别。时间复杂度为 O(log2n) 的算法运行时间为下面那条线。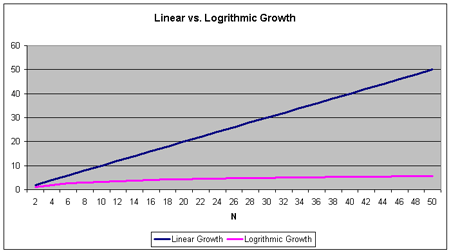
从上图可以看出,O(log2n) 曲线几乎是水平的,随着 n 值的增加,曲线增长十分缓慢。举例来说,查找一个具有 1000 个元素的数组,需要查询 1000 个元素,而查找一个具有 1000 个元素的 BST 树,仅需查询不到10 个节点(log21024 = 10)。查找代码:
/** * 搜索二分搜索树中是否包含元素 e * 时间复杂度 O(log n) * @param node * @param e * @return */ public static boolean contains(Node node,int e) { if(node==null) { return false; }else if(node.data == e) { return true; }else if(node.data > e) { return contains(node.left,e); }else { return contains(node.right,e); } }
特殊情况说明
而实际上,对于 BST 查找算法来说,其十分依赖于树中节点的拓扑结构,也就是节点间的布局关系。下图描绘了一个节点插入顺序为 20, 50, 90, 150, 175, 200 的 BST 树。这些节点是按照递升顺序被插入的,结果就是这棵树没有广度(Breadth)可言。也就是说,它的拓扑结构其实就是将节点排布在一条线上,而不是以扇形结构散开,所以查找时间也为 O(n)。<br />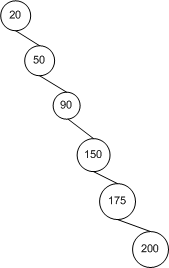<br /> 当 BST 树中的节点以扇形结构散开时,对它的插入、删除和查找操作最优的情况下可以达到亚线性的运行时间 O(log2n)。因为当在 BST 中查找一个节点时,每一步比较操作后都会将节点的数量减少一半。尽管如此,如果拓扑结构像上图中的样子时,运行时间就会退减到线性时间 O(n)。因为每一步比较操作后还是需要逐个比较其余的节点。也就是说,在这种情况下,在 BST 中查找节点与在数组(Array)中查找就基本类似了。<br /> 因此,**BST 算法查找时间依赖于树的拓扑结构。最佳情况是 O(log2n),而最坏情况是 O(n)。**<br />**该问题如何解决,我们会在“红黑树”中进行说明。**
4、对二分搜索树进行操作:
4.1 插入节点
我们不仅需要了解如何在二分搜索树中查找一个节点,还需要知道如何在二分搜索树中插入和删除一个节点。<br />当向树中插入一个新的节点时,该节点将总是作为叶子节点。所以,最困难的地方就是如何找到该节点的父节点。类似于查找算法中的描述,我们将这个新的节点称为节点 n,而遍历的当前节点称为节点 c。开始时,节点 c 为 BST 的根节点。则定位节点 n 父节点的步骤如下:
- 如果节点 c 为空,则节点 c 的父节点将作为节点 n 的父节点。如果节点 n 的值小于该父节点的值,则节点 n 将作为该父节点的左孩子;否则节点 n 将作为该父节点的右孩子。
- 比较节点 c 与节点 n 的值。
- 如果节点 c 的值与节点 n 的值相等,则说明用户在试图插入一个重复的节点。解决办法可以是直接丢弃节点 n,或者可以抛出异常。
- 如果节点 n 的值小于节点 c 的值,则说明节点 n 一定是在节点 c 的左子树中。则将父节点设置为节点 c,并将节点 c 设置为节点 c 的左孩子,然后返回至第 1 步。
- 如果节点 n 的值大于节点 c 的值,则说明节点 n 一定是在节点 c 的右子树中。则将父节点设置为节点 c,并将节点 c 设置为节点 c 的右孩子,然后返回至第 1 步。
当合适的节点找到时,该算法结束。从而使新节点被放入 BST 中成为某一父节点合适的孩子节点。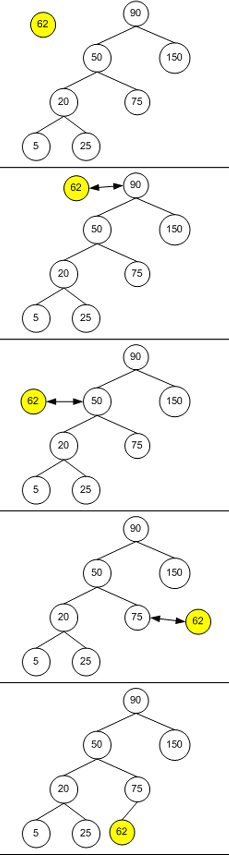
BST 的插入算法的复杂度与查找算法的复杂度是一样的:最佳情况是 O(log2n),而最坏情况是 O(n)。因为它们对节点的查找定位策略是相同的。
实现代码
class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
}
/**
* 二分搜索树(不能有重复数据)
*/
class Bst {
private Node root; // 根节点
private int size;
public Bst() {
root = null;
size = 0;
}
// 向二分搜索树中添加元素(使用递归方式)
public void add(int value) {
root = add(root, value);
}
// 向以node为根的二分搜索树中插入元素
private Node add(Node node, int value) {
// 如果已经深入到一个空节点时,也就意味着肯定要添加一个新元素了。(这个作为结束条件)
if (node == null) {
size++;
return new Node(value);
}
// 如果相等,则什么都不做(因为不能有重复数据)
if (value < node.value) {
node.left = add(node.left, value);
} else if (value > node.value) {
node.right = add(node.right, value);
}
return node;
}
}
4.2.查找节点
实现代码
// 查找
public boolean contains(int value) {
return contains(root, value);
}
private boolean contains(Node node, int value) {
if (node == null) {
return false;
}
if (value < node.value) {
return contains(node.left, value);
} else if (value > node.value) {
return contains(node.right, value);
} else {
return true;
}
}
4.3.删除最大值最小值节点
删除最大值和最小值:
根据二分搜索树的特点:从根节点开始一直向左走,直到没有左子节点时就是最小值。
同理,从根节点开始一直向右走,直到没有右子节点时就是最大值。
最小值特点:要么是左边最后一个叶子节点,要么是左边的一个只有右节点的节点。 最大值特点:要么是右边最后一个叶子节点,要么是有边的一个只有左节点的节点。
因此,当删除一个最大值或最小值时,可以直接使用左节点或右节点来替换删除的节点。
实现代码
// 删除最小值(先寻找最小元素,然后在删除)
// 寻找最小值
public int minimum() {
if (size == 0) {
// 不合法的参数异常
throw new IllegalArgumentException("BST is empty!");
}
return minimum(root).value;
}
private Node minimum(Node node) {
if (node.left == null) {
return node;
}
return minimum(node.left);
}
// 删除最小值
public int removeMin() {
int ret = minimum();
root = removeMin(root);
return ret;
}
private Node removeMin(Node node) {
// node.left==null时,node即为最左边节点
if (node.left == null) {
// 如果当前要删除的节点有右子树,那么还要将右子树节点进行替换
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 递归查找最左边节点
node.left = removeMin(node.left);
return node;
}
// 删除最大值(先寻找最大元素,然后在删除)
// 寻找最大值
public int maximum() {
if (size == 0) {
throw new IllegalArgumentException("BST is empty!");
}
return maximum(root).value;
}
private Node maximum(Node node) {
if (node.right == null) {
return node;
}
return maximum(node.right);
}
// 删除最大值
public int removeMax() {
int ret = maximum();
root = removeMax(root);
return ret;
}
private Node removeMax(Node node) {
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
4.2 删除节点
从 BST 中删除节点比插入节点难度更大。因为删除一个非叶子节点,就必须选择其他节点来填补因删除节点所造成的树的断裂。如果不选择节点来填补这个断裂,那么就违背了 BST 的性质要求。
当删除二叉树中的一个带有左右节点的节点时,可以遵循 Hibbard Deletion 规则:
- 寻找比当前要删除的节点大且距离最近的节点来替换,这个节点就是当前要删除节点的右子树下的左子树节点(最底层的)
- 因为它一定是比当前要删除的节点大,而且是最小的最大值。 或者说:用当前要删除的节点的右边的最小值来替换当前节点。
和查找、插入算法类似,删除算法的运行时间也与 BST 的拓扑结构有关,最佳情况是 O(log2n),而最坏情况是 O(n)。
实现代码
// 删除
public void remove(int value) {
remove(root, value);
}
private Node remove(Node node, int value) {
if (node == null) {
return null;
}
if (value < node.value) {
node.left = remove(node.left, value);
return node;
} else if (value > node.value) {
node.right = remove(node.right, value);
return node;
} else {
// 待删除节点左子树为空的情况
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 待删除节点右子树为空的情况
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 待删除节点左右子树都不为空的情况(找到后继节点)
Node successor = minimum(node.right);
// 注意,removeMin中已经做了size--,所以下面就不在size--了
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
4.3 遍历节点
对于线性的连续的数组来说,遍历数组采用的是单向的迭代法。从第一个元素开始,依次向后迭代每个元素。而 BST 则有三种常用的遍历方式:
- 前序遍历(Perorder traversal)
- 中序遍历(Inorder traversal)
后序遍历(Postorder traversal)
当然,这三种遍历方式的工作原理是类似的。它们都是从根节点开始,然后访问其子节点。区别在于遍历时,访问节点本身和其子节点的顺序不同。<br />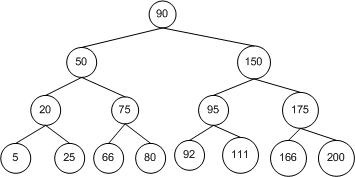前序遍历(Perorder traversal)
前序遍历从当前节点(节点 c)开始访问,然后访问其左孩子,再访问右孩子。开始时,节点 c 为 BST 的根节点。算法如下:
- 访问节点 c;
- 对节点 c 的左孩子重复第 1 步;
- 对节点 c 的右孩子重复第 1 步;
则上图中树的遍历结果为:90, 50, 20, 5, 25, 75, 66, 80, 150, 95, 92, 111, 175, 166, 200。
中序遍历(Inorder traversal)
中序遍历是从当前节点(节点 c)的左孩子开始访问,再访问当前节点,最后是其右节点。开始时,节点 c 为 BST 的根节点。算法如下:
- 访问节点 c 的左孩子;
- 对节点 c 重复第 1 步;
- 对节点 c 的右孩子重复第 1 步。
则上图中树的遍历结果为:5, 20, 25, 50, 66, 75, 80, 90, 92, 95, 111, 150, 166, 175, 200。
后序遍历(Postorder traversal)
后序遍历首先从当前节点(节点 c)的左孩子开始访问,然后是右孩hib子,最后才是当前节点本身。开始时,节点 c 为 BST 的根节点。算法如下:
- 访问节点 c 的左孩子;
- 对节点 c 的右孩子重复第1 步;
- 对节点 c 重复第 1 步;
则上图中树的遍历结果为:5, 25, 20, 66, 80, 75, 50, 92, 111, 95, 166, 200, 175, 150, 90。
5、BST综合代码
import java.util.LinkedList;
import java.util.Queue;
class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
}
/**
* 二分搜索树(不能有重复数据)
*/
class Bst {
private Node root; // 根节点
private int size;
public Bst() {
root = null;
size = 0;
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
// 向二分搜索树中添加元素(使用递归方式)
public void add(int value) {
root = add(root, value);
}
// 向以node为根的二分搜索树中插入元素
private Node add(Node node, int value) {
// 如果已经深入到一个空节点时,也就意味着肯定要添加一个新元素了。(这个作为结束条件)
if (node == null) {
size++;
return new Node(value);
}
// 如果相等,则什么都不做(因为不能有重复数据)
if (value < node.value) {
node.left = add(node.left, value);
} else if (value > node.value) {
node.right = add(node.right, value);
}
return node;
}
// 查找
public boolean contains(int value) {
return contains(root, value);
}
private boolean contains(Node node, int value) {
if (node == null) {
return false;
}
if (value < node.value) {
return contains(node.left, value);
} else if (value > node.value) {
return contains(node.right, value);
} else {
return true;
}
}
// 前序遍历
public void preOrder() {
preOrder(root);
System.out.print("\n");
}
private void preOrder(Node node) {
if (node == null) {
return;
}
System.out.print(node.value + " ");
preOrder(node.left);
preOrder(node.right);
}
// 中序遍历
public void inOrder() {
inOrder(root);
System.out.print("\n");
}
private void inOrder(Node node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.print(node.value + " ");
inOrder(node.right);
}
// 后序遍历
public void postOrder() {
postOrder(root);
System.out.print("\n");
}
private void postOrder(Node node) {
if (node == null) {
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.print(node.value + " ");
}
// 层序遍历
public void levelOrder() {
Queue<Node> queue = new LinkedList();
queue.add(root);
while (!queue.isEmpty()) {
Node cur = queue.remove();
System.out.print(cur.value + " ");
if (cur.left != null) {
queue.add(cur.left);
}
if (cur.right != null) {
queue.add(cur.right);
}
}
System.out.print("\n");
}
/**
* 删除最大值和最小值: 根据二分搜索树的特点:从根节点开始一直向左走,直到没有左子节点时就是最小值。
* 同理,从根节点开始一直向右走,直到没有右子节点时就是最大值。
*
* 最小值特点:要么是左边最后一个叶子节点,要么是左边的一个只有右节点的节点。 最大值特点:要么是右边最后一个叶子节点,要么是有边的一个只有左节点的节点。
* 因此,当删除一个最大值或最小值时,可以直接使用左节点或右节点来替换删除的节点。
*/
// 删除最小值(先寻找最小元素,然后在删除)
// 寻找最小值
public int minimum() {
if (size == 0) {
// 不合法的参数异常
throw new IllegalArgumentException("BST is empty!");
}
return minimum(root).value;
}
private Node minimum(Node node) {
if (node.left == null) {
return node;
}
return minimum(node.left);
}
// 删除最小值
public int removeMin() {
int ret = minimum();
root = removeMin(root);
return ret;
}
private Node removeMin(Node node) {
// node.left==null时,node即为最左边节点
if (node.left == null) {
// 如果当前要删除的节点有右子树,那么还要将右子树节点进行替换
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 递归查找最左边节点
node.left = removeMin(node.left);
return node;
}
// 删除最大值(先寻找最大元素,然后在删除)
// 寻找最大值
public int maximum() {
if (size == 0) {
throw new IllegalArgumentException("BST is empty!");
}
return maximum(root).value;
}
private Node maximum(Node node) {
if (node.right == null) {
return node;
}
return maximum(node.right);
}
// 删除最大值
public int removeMax() {
int ret = maximum();
root = removeMax(root);
return ret;
}
private Node removeMax(Node node) {
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
/**
* 当删除二叉树中的一个带有左右节点的节点时,可以遵循 Hibbard Deletion 规则:
* 寻找比当前要删除的节点大且距离最近的节点来替换,这个节点就是当前要删除节点的右子树下的左子树节点(最底层的),
* 因为它一定是比当前要删除的节点大,而且是最小的最大值。 或者说:用当前要删除的节点的右边的最小值来替换当前节点。
*/
// 删除
public void remove(int value) {
remove(root, value);
}
private Node remove(Node node, int value) {
if (node == null) {
return null;
}
if (value < node.value) {
node.left = remove(node.left, value);
return node;
} else if (value > node.value) {
node.right = remove(node.right, value);
return node;
} else {
// 待删除节点左子树为空的情况
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 待删除节点右子树为空的情况
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 待删除节点左右子树都不为空的情况(找到后继节点)
Node successor = minimum(node.right);
// 注意,removeMin中已经做了size--,所以下面就不在size--了
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
}
public class Test {
public static void main(String[] args) {
Bst bst = new Bst();
System.out.println(bst.isEmpty());
System.out.println(bst.size());
int[] nums = { 5, 1, 6, 8, 3, 0, 7, 2, 9, 4 };
for (int num : nums) {
bst.add(num);
}
///////////////////////////
// 5 //
// / \ //
// 1 6 //
// / \ \ //
// 0 3 8 //
// / \ / \ //
// 2 4 7 9 //
///////////////////////////
System.out.println(bst.isEmpty());
System.out.println(bst.size());
System.out.println(bst.contains(10));
// 前序遍历
bst.preOrder(); // 5,1,0,3,2,4,6,8,7,9
// 中序遍历
bst.inOrder(); // 0,1,2,3,4,5,6,7,8,9
// 后序遍历
bst.postOrder(); // 0,2,4,3,1,7,9,8,6,5
// 层序遍历
bst.levelOrder(); // 5,1,6,0,3,8,2,4,7,9
bst.removeMin();
bst.removeMax();
bst.remove(6);
bst.remove(2);
bst.inOrder();
}
}