分析

题目：构造无向图如下

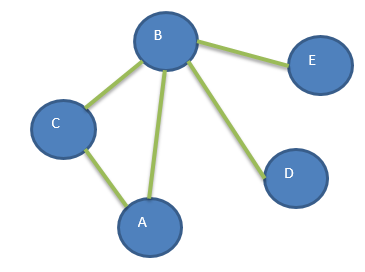
说明
(1) 存储顶点String 使用 ArrayList
(2) 保存矩阵 int[][] edges

编写程序，输出为邻接矩阵如下：

说明
(1) 1 表示能够直接连接
(2) 0 表示不能直接连接

代码实现

import java.util.ArrayList;
import java.util.Arrays;
public class Graph {
    private ArrayList<String> vertexList; // 存储顶点集合
    private int[][] edges; // 存储图对应的邻结矩阵
    private int numOfEdges; // 表示边的数目
    // 构造器，初始化矩阵和vertexList
    public Graph(int n) {
        edges = new int[n][n];
        vertexList = new ArrayList<String>(n);
        numOfEdges = 0;
    }
    // 返回顶点的个数
    public int getNumOfVertex() {
        return vertexList.size();
    }
    // 得到边的数目
    public int getNumOfEdges() {
        return numOfEdges;
    }
    // 返回结点i(下标)对应的顶点 0->"A" 1->"B" 2->"C"
    public String getValueByIndex(int i) {
        return vertexList.get(i);
    }
    // 返回v1和v2的权值
    public int getWeight(int v1, int v2) {
        return edges[v1][v2];
    }
    // 显示图对应的矩阵
    public void showGraph() {
        for (int[] link : edges) {
            System.err.println(Arrays.toString(link));
        }
    }
    // 插入结点
    public void insertVertex(String vertex) {
        vertexList.add(vertex);
    }
    // 添加边
    /**
     * @param v1     表示点的下标即使第几个顶点 "A"-"B" "A"->0 "B"->1
     * @param v2     第二个顶点对应的下标
     * @param weight 表示权重
     */
    public void insertEdge(int v1, int v2, int weight) {
        // 因为构建的是无向图，所以这里直接设置顶点之间的双向边
        edges[v1][v2] = weight;
        edges[v2][v1] = weight;
        numOfEdges++;
    }
    public static void main(String[] args) {
        // 顶结点的个数
        int n = 5;
        String Vertexs[] = { "A", "B", "C", "D", "E" };
        // 创建图对象
        Graph graph = new Graph(n);
        // 循环的添加顶点
        for (String vertex : Vertexs) {
            graph.insertVertex(vertex);
        }
        // 添加边
        // A-B A-C B-C B-D B-E
        graph.insertEdge(0, 1, 1); // A-B
        graph.insertEdge(0, 2, 1); //
        graph.insertEdge(1, 2, 1); //
        graph.insertEdge(1, 3, 1); //
        graph.insertEdge(1, 4, 1); //
        // 获取顶点的个数
        System.out.println("顶点个数："+graph.getNumOfVertex());
        // 获取边的数目
        System.out.println("边个数："+graph.getNumOfEdges());
        // 获取结点i(下标)对应的顶点 0->"A" 1->"B" 2->"C"
        System.out.println("结点下标对应的顶点："+graph.getValueByIndex(1));
        // 获取v1和v2的权值
        System.out.println("权值："+graph.getWeight(1,2));
        // 显示邻结矩阵
        graph.showGraph();
    }
}