深度优先和广度优先这两个概念不止局限于二叉树，它们更是一种抽象的算法思想，决定了访问某些复杂数据结构的顺序。在访问树、图，或其他一些复杂数据结构时，这两个概念常常被使用到。<br />      所谓深度优先，顾名思义，就是偏向于纵深，“一头扎到底”的访问方式。可能这种说法有些抽象，下面就通过前面学过的二叉树的前序遍历、中序遍历、后序遍历，来看一看深度优先是怎么回事吧。

使用前序遍历为例

二叉树的前序遍历，输出顺序是根节点、左子树、右子树。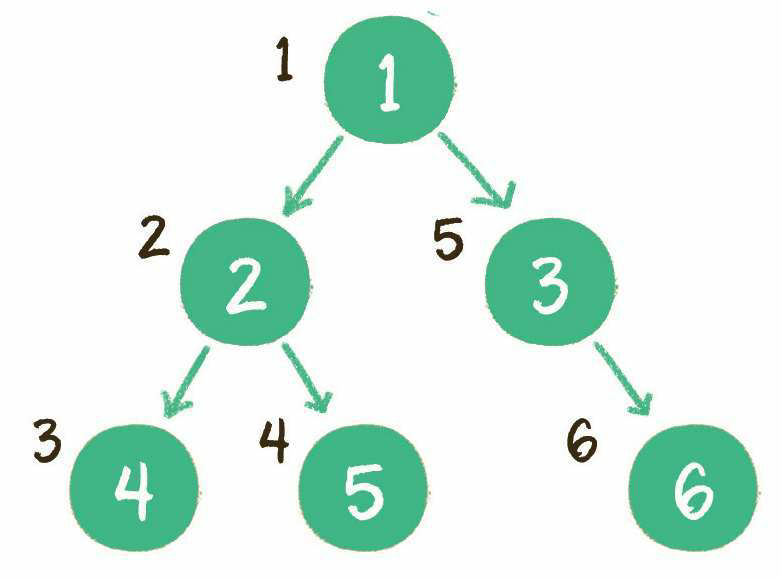

上图就是一个二叉树的前序遍历，每个节点左侧的序号代表该节点的输出顺序，详细步骤如下。
1. 首先输出的是根节点1。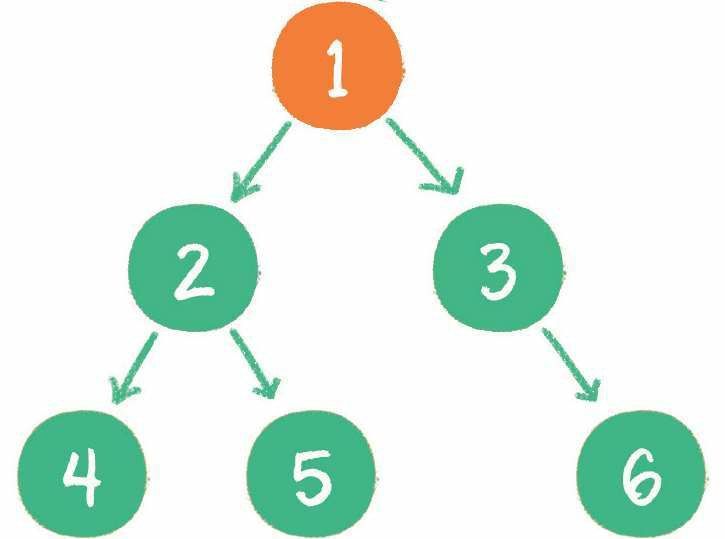

2. 由于根节点1存在左孩子，输出左孩子节点2。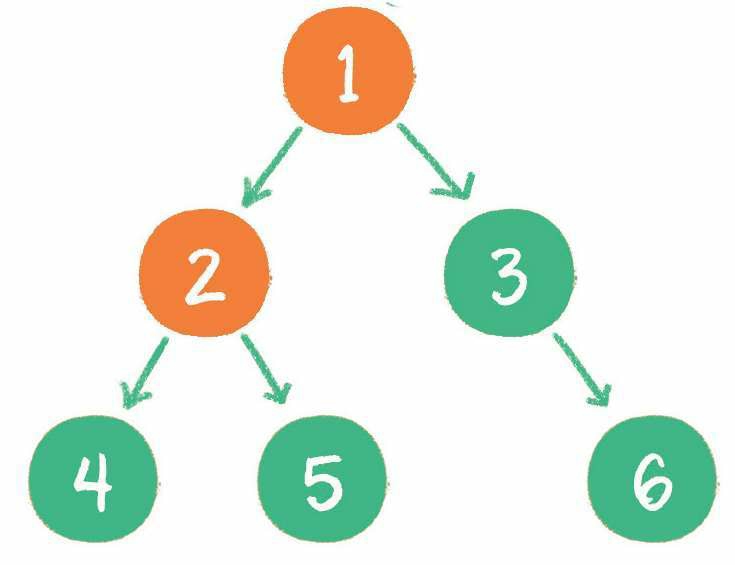

3. 由于节点2也存在左孩子，输出左孩子节点4。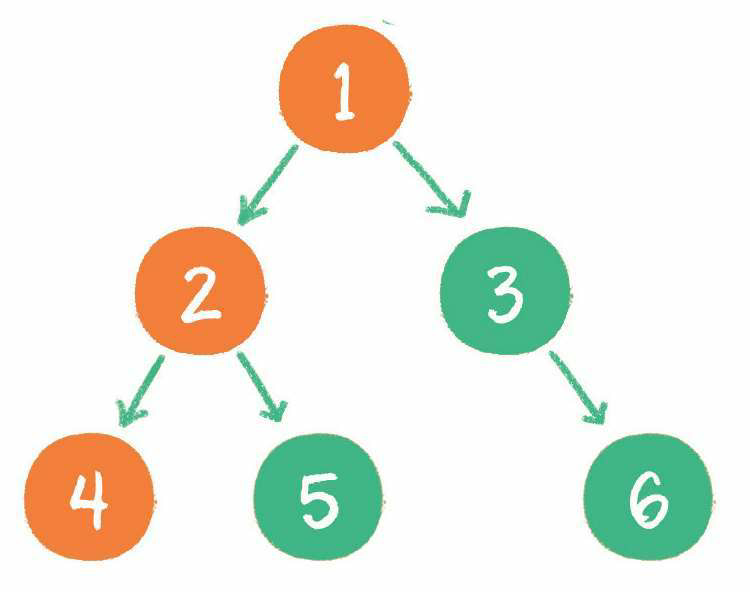

4. 节点4既没有左孩子，也没有右孩子，那么回到节点2，输出节点2的右孩子节点5。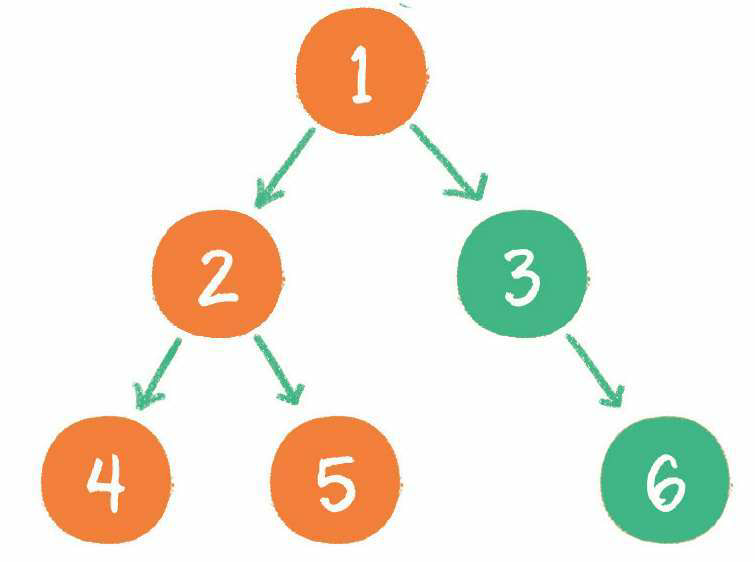

5. 节点5既没有左孩子，也没有右孩子，那么回到节点1，输出节点1的右孩子节点3。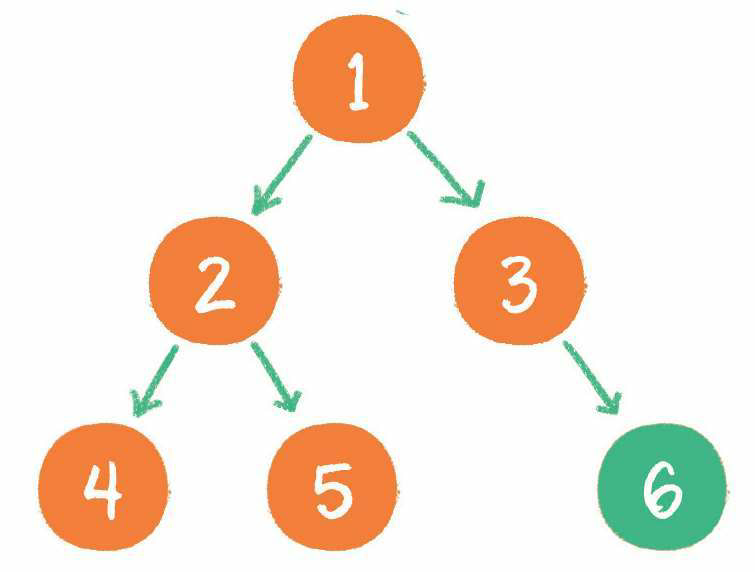

6. 节点3没有左孩子，但是有右孩子，因此输出节点3的右孩子节点6。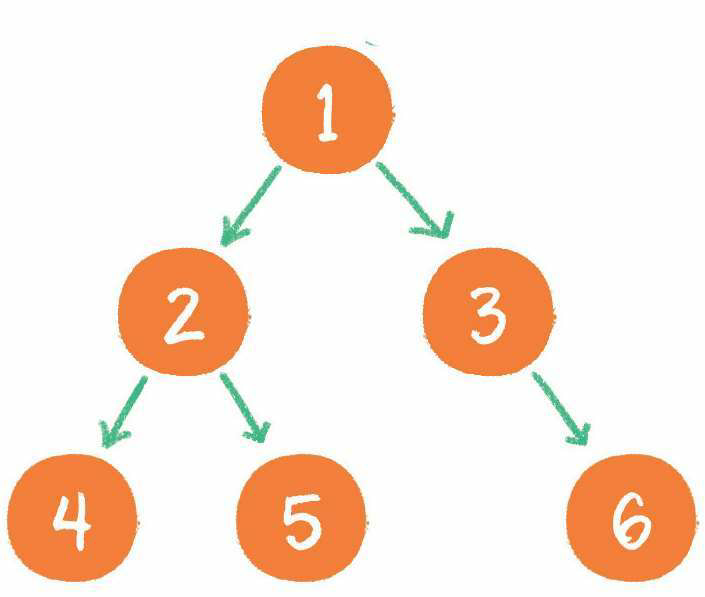

到此为止，所有的节点都遍历输出完毕。