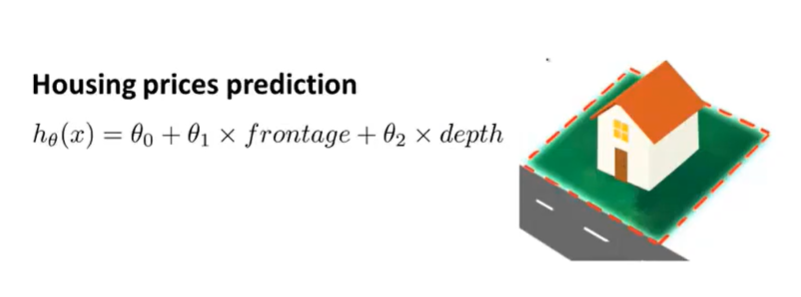
目的
高阶特征
也可以将面积作为特征函数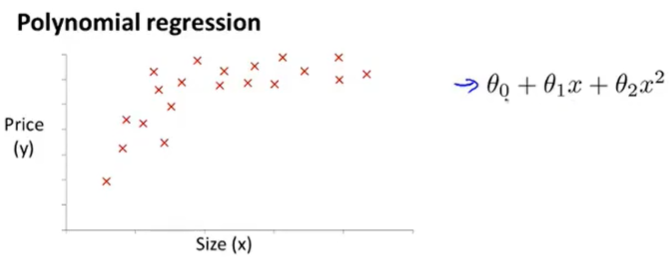
预测函数中有更高阶的特征量
特征缩放将更重要（幂会放大/缩小数据范围）
需要使得值具有可比性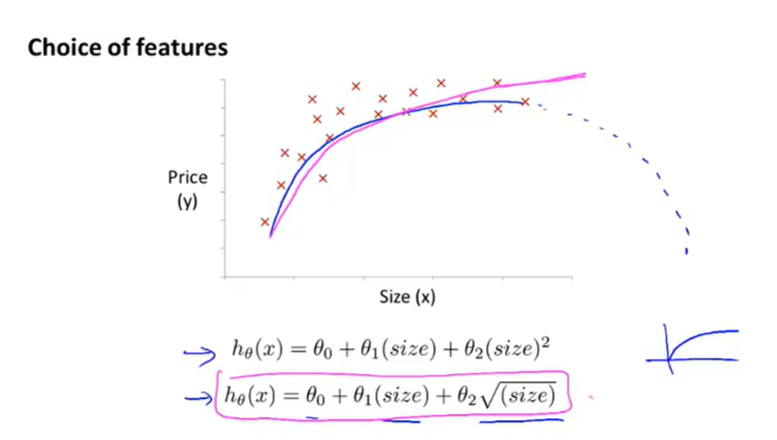
需要选取合适的特征函数
比如二次函数最终会下降，不适合房价预测上
可以通过某种算法自动寻找合适的描述
正规方程
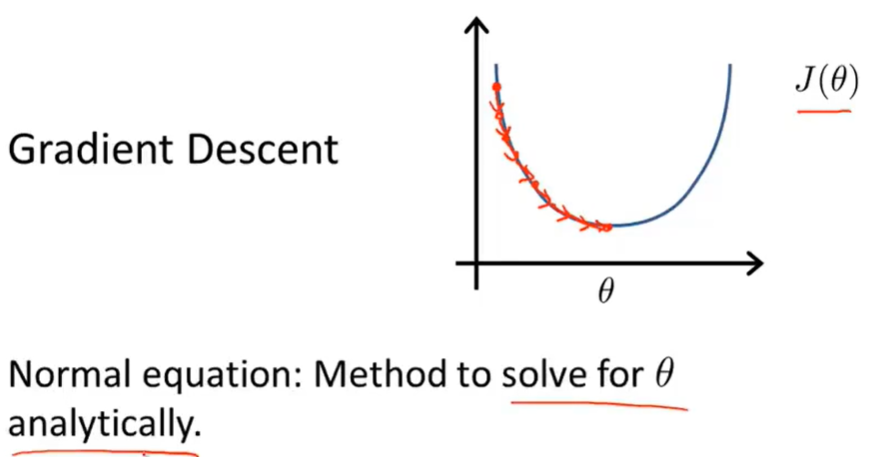
不需要迭代，通过解析方程直接得到最优解
当特征函数为1维时，直接对代价函数求导，取导数零值处，求最小值
但当特征函数为n+1维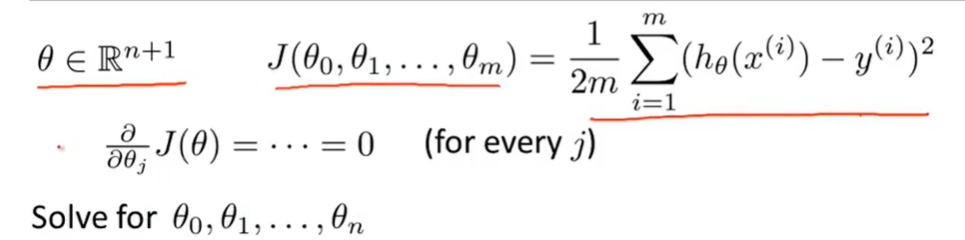
需要逐个对模型参数θ求偏导，然后置零，求出参数
这个过程较为复杂
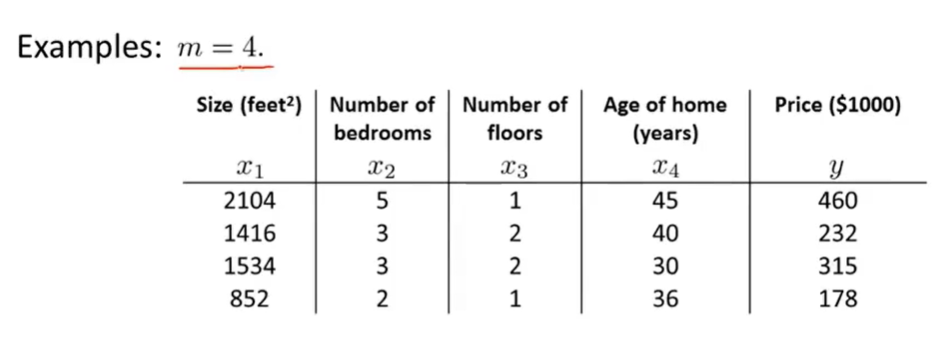
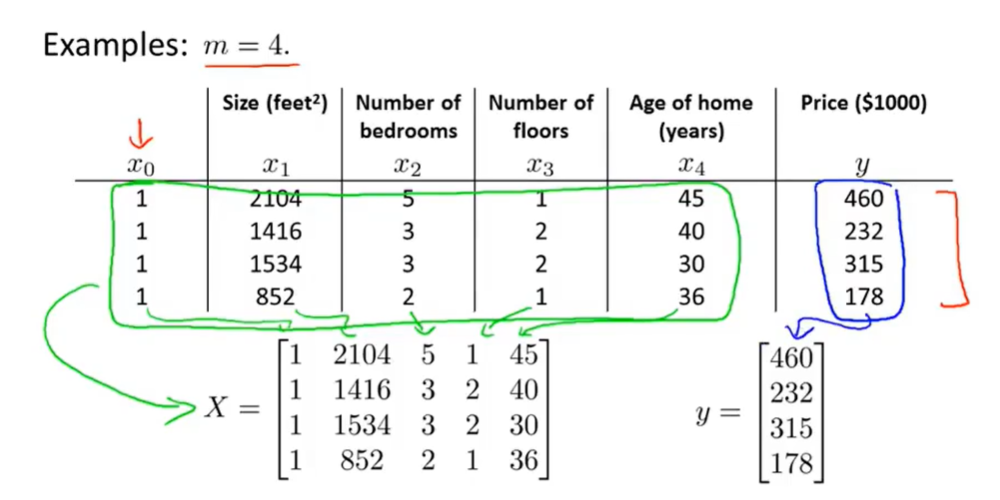
即可求得代价函数最小的模型参数
正规方程法无需特征缩放
对比
特征变量不多（小于1W）正规方程法可能更合适
但在大量特征函数下，梯度下降法会更快
- 如果正规方程法中的矩阵不可逆
- 即遇到奇异矩阵
pinv：求伪逆矩阵，即使不可逆也可求解
inv：求逆矩阵
不可逆矩阵发生的情况
- 多余的特征变量（线性相关的特征变量考虑删掉）
- 样本数少于特征变量（考虑删除特征或正则化）
若有收获，就点个赞吧
0 人点赞
