基本概念

image.png

image.png

步骤分析

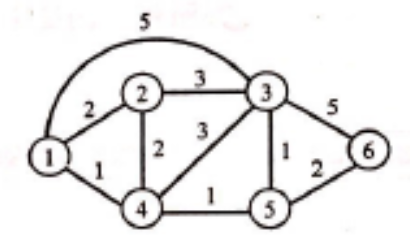
【数据结构】最短路径算法Dijkstra - 图3

  • 图的输入 | | n1 | n2 | n3 | n4 | n5 | n6 | | —- | —- | —- | —- | —- | —- | —- | | n1 | 0 | 2 | 1 | 5 | inf | inf | | n2 | 2 | 0 | 2 | 3 | inf | inf | | n3 | 1 | 2 | 0 | 3 | 1 | inf | | n4 | 5 | 3 | 3 | 0 | 1 | 5 | | n5 | inf | inf | 1 | 1 | 0 | 2 | | n6 | inf | inf | inf | 5 | 2 | 0 |

  • 迭代过程

    • 定义如下记号

【数据结构】最短路径算法Dijkstra - 图4 | N’ | D(2),P(2) | D(3),P(3) | D(4),P(4) | D(5),P(5) | D(6),P(6) | | —- | —- | —- | —- | —- | —- | | 1 | [D(2) Vs D(1)+C(1,2)]
[2 = 0 + 2]
D(2),P(2) = 2,1 | [D(3) Vs D(1)+C(1,3)]
[1 = 0 + 1]
D(3),P(3) = 1,1(MIN) | [D(4) Vs D(1)+C(1,4)]
[5 = 0 + 5]
D(4),P(4) = 5,1 | [D(5) Vs D(1)+C(1,5)]
[inf = 0 + inf]
D(5),P(5) = inf | [D(6) Vs D(1)+C(1,6)]
[inf = 0 + inf]
D(6),P(6) = inf | | 1,3 | [D(2) Vs D(3)+C(3,2)]
[2 < 1 + 2]
D(2),P(2) = 保留2,1 | | [D(4) Vs D(3)+C(3,4)]
[5 > 1 + 3]
D(4),P(4) = 更新4,3 | [D(5) Vs D(3)+C(3,5)]
[inf < 1 + 1]
D(5),P(5) = 更新2,3(MIN) | [D(6) Vs D(3)+C(3,6)]
[inf = inf]
D(6),P(6) = inf | | 1,3,5 | [D(2) Vs D(5)+C(5,2)]
[2 < 2 + inf]
D(2),P(2) = 保留2,1(MIN) | | [D(4) Vs D(5)+C(5,4)]
[4 > 2 + 1]
D(4),P(4) = 更新3,5 | | [D(6) Vs D(5)+C(5,6)]
[inf > 2 + 2]
D(6),P(6) = 更新4,5 | | 1,3,5,2 | | | [D(4) Vs D(2)+C(2,4)]
[3 < 2 + 3]
D(4),P(4) = 保留3,5(MIN) | | [D(6) Vs D(2)+C(2,6)]
[4 < 2 + inf]
D(6),P(6) = 保留4,5 | | 1,3,5,2,4 | | | | | [D(6) Vs D(4)+C(4,6)]
[4 < 3 + 5]
D(6),P(6) = 保留4,5(MIN) | | 1,3,5,2,4,6 | | | | | |

C++实现

  1. /*
  2.  * Copyright (c) 2020 - ~, Wang Xi
  3.  *
  4.  * DIJKSTRA ALGORITHM
  5.  * Used in C++
  6.  *
  7.  * Change Logs:
  8.  * Date           Author       Notes                Mail
  9.  * 2021-04-17     WangXi       first version        WangXi_chn@foxmail.com
  10.  */
  12. #include <iostream>
  13. #include <string>
  15. using namespace std;
  17. // Record the calculate result and be used in iteration
  18. struct Result
  19. {
  20.     string path;
  21.     int value;
  22.     bool visit;
  23. };
  25. class Graph
  26. {
  27. public:
  28.     int _inf_ = 10000;
  29.     int vexnum = 6;
  30.     int soucenode = 1;
  31.     int arc[6][6] = {
  32.                         {0,        2,        1,        5,    _inf_,    _inf_},
  33.                         {2,        0,        2,        3,    _inf_,    _inf_},
  34.                         {1,        2,        0,        3,        1,    _inf_},
  35.                         {5,        3,        3,        0,        1,        5},
  36.                         {_inf_,    _inf_,    1,        1,        0,        2},
  37.                         {_inf_, _inf_,    _inf_,    5,        2,        0}
  38.     };;
  39.     Result result[6];
  41.     Graph(void);
  42.     void GraphInit();
  43.     string GraphPrint();
  44.     string PathPrint();
  45.     void Dijkstra();
  47. };
  49. Graph::Graph(void)
  50. {
  51.     this->GraphInit();
  52.     cout << this->GraphPrint() << endl;
  53.     this->Dijkstra();
  54.     cout << this->PathPrint() << endl;
  55. }
  57. void Graph::GraphInit() {
  58.     for (int i = 0; i < this->vexnum; i++)
  59.     {
  60.         this->result[i].path = "";
  61.         this->result[i].value = 0;
  62.         this->result[i].visit = false;
  63.     }
  64. }
  66. string Graph::GraphPrint()
  67. {
  68.     string result = "图的邻接矩阵为：\r\n";
  69.     int count_row = 0;
  70.     int count_col = 0;
  72.     while (count_row != this->vexnum)
  73.     {
  74.         count_col = 0;
  75.         while (count_col != this->vexnum)
  76.         {
  77.             if (arc[count_row][count_col] == this->_inf_)
  78.                 result = result + "∞" + "\t";
  79.             else
  80.                 result = result + std::to_string(arc[count_row][count_col]) + "\t";
  82.             ++count_col;
  83.         }
  84.         ++count_row;
  85.         result += "\r\n";
  86.     }
  87.     result += "\r\n";
  89.     return result;
  90. }
  92. string Graph::PathPrint()
  93. {
  94.     string str;
  96.     str = "以D" + std::to_string(this->soucenode) + "为起点的最短路径为：\r\n";
  97.     for (int i = 0; i != this->vexnum; i++)
  98.     {
  99.         if (result[i].value != _inf_)
  100.             str += result[i].path + "=" + std::to_string(result[i].value) + "\r\n";
  101.         else
  102.         {
  103.             str += result[i].path + "是无最短路径的" + "\r\n";
  104.         }
  105.     }
  107.     return str;
  108. }
  110. void Graph::Dijkstra()
  111. {
  112.     /* Config result array */
  113.     int i;
  114.     for (i = 0; i < this->vexnum; i++)
  115.     {
  116.         /* Set up default path */
  117.         this->result[i].path = "D" + std::to_string(this->soucenode) + "-->D" + std::to_string(i + 1);
  118.         result[i].value = arc[this->soucenode - 1][i];
  119.     }
  121.     /* Set up start to start node value */
  122.     result[this->soucenode - 1].value = 0;
  123.     result[this->soucenode - 1].visit = true;
  125.     int count = 1;
  127.     /* Calculate the rest node */
  128.     while (count != this->vexnum)
  129.     {
  130.         //temp: the index of node has min length
  131.         //min: the min path's length value 
  132.         int temp = 0;
  133.         int min = _inf_;
  134.         for (i = 0; i < this->vexnum; i++)
  135.         {
  136.             if (!result[i].visit && result[i].value < min)
  137.             {
  138.                 min = result[i].value;
  139.                 temp = i;
  140.             }
  141.         }
  143.         /* Mark the node had been choosen */
  144.         result[temp].visit = true;
  145.         ++count;
  146.         for (i = 0; i < this->vexnum; i++)
  147.         {
  148.             if (!result[i].visit && arc[temp][i] != _inf_ && (result[temp].value + arc[temp][i]) < result[i].value)
  149.             {
  150.                 /* Find the better path, updata the result array */
  151.                 result[i].value = result[temp].value + arc[temp][i];
  152.                 result[i].path = result[temp].path + "-->D" + to_string(i + 1);
  153.             }
  154.         }
  155.     }
  157. }
  159. int main()
  160. {
  161.     Graph graph;
  162.     return 0;
  163. }
  167. /************************ (C) COPYRIGHT 2021 WANGXI **************END OF FILE****/