监督学习

基本概念

常用表示
m = Number of training examples
x’s = “input” variable/features
y’s = “output” variable/features
(x,y)=one traning example
(x^(i),y^(i))=i^th traning example

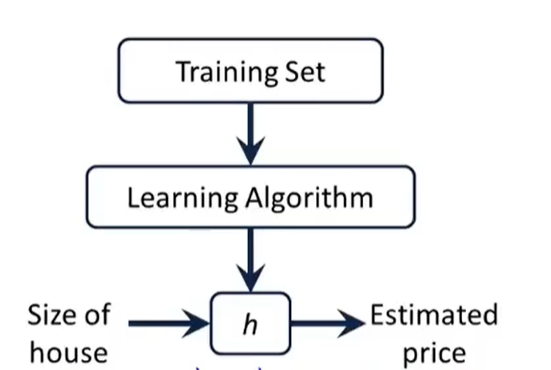
h: hypothesis假设函数
如：
Univariable linear regression 单变量线性回归

代价函数

cost function

θ：模型参数
选择合适的模型参数使得h(x)-y最小化的问题
设定代价函数
求J的最小值
平方误差函数

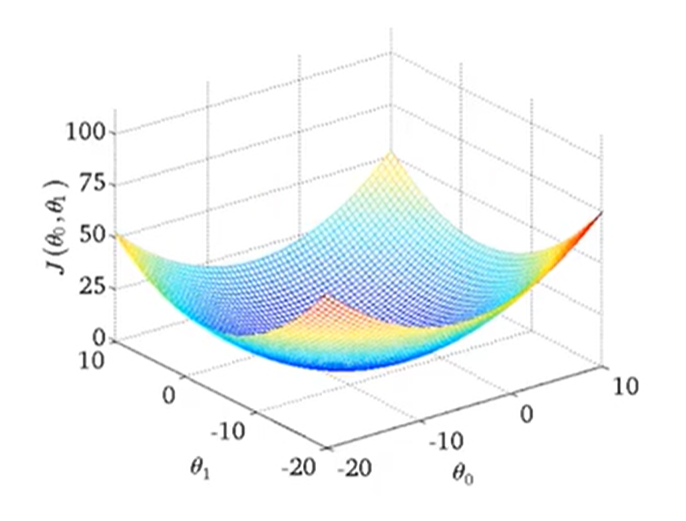
梯度下降

gradient descent

注意同步更新
“:=”计算机赋值号
“=”真假判断
α：learning rate，即步长
学习率太小：梯度下降较慢
学习率过大：梯度下降越过最低点。无法收敛converge，甚至发散diverge

计算结果

将J带入求偏导可得

注意同步更新，而不是第一个计算结果影响到第二个

凸函数没有局部最优，只有一个总体最优

因为要对整个数据集遍历，所以该算法是全览了整个数据集

也可以使用正规方程组法，无需迭代，直接计算出最小值，但梯度下降法更适合较大数据集