简介

要预测的变量 y 是一个离散值
logistic回归算法
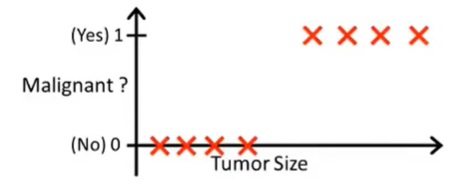
image.png
image.png
image.png
如果采用线性回归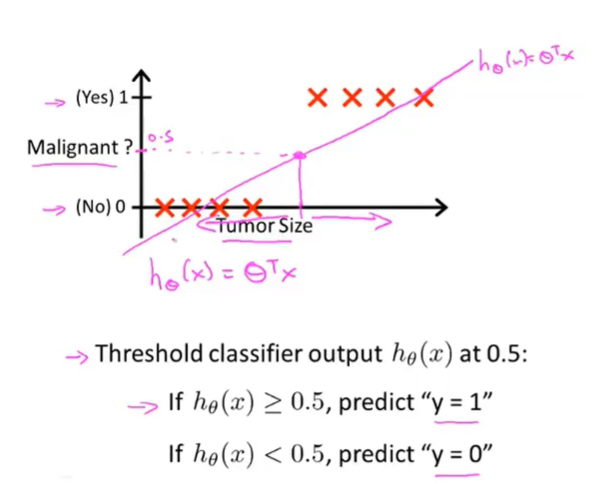
image.png
似乎也可以描述，但是如果训练集分布不均匀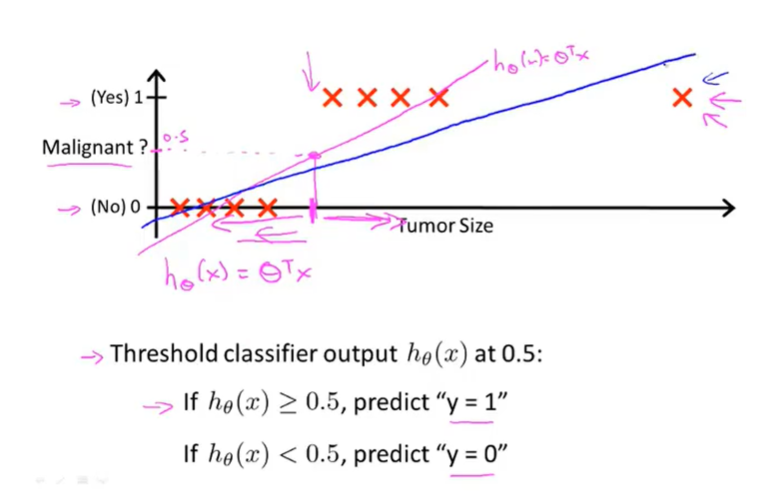
image.png
效果变差（加了例子导致线性回归得到了更糟糕的结果）
因此线性回归问题将不适用于分类问题
线性回归的输出值可能会超出分类问题的取值范围

假设陈述

数学模型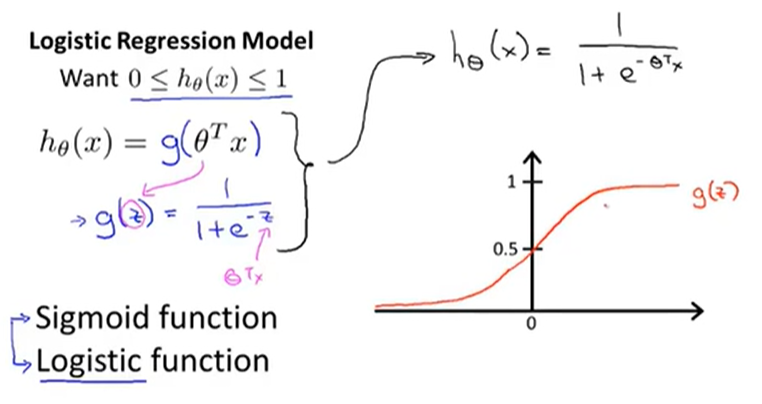
image.png
实现了限定假设函数【机器学习】分类问题 - 图7在0-1之间
image.png
假设函数的输出值是个基于模型参数 θ 时，y=1 的概率值
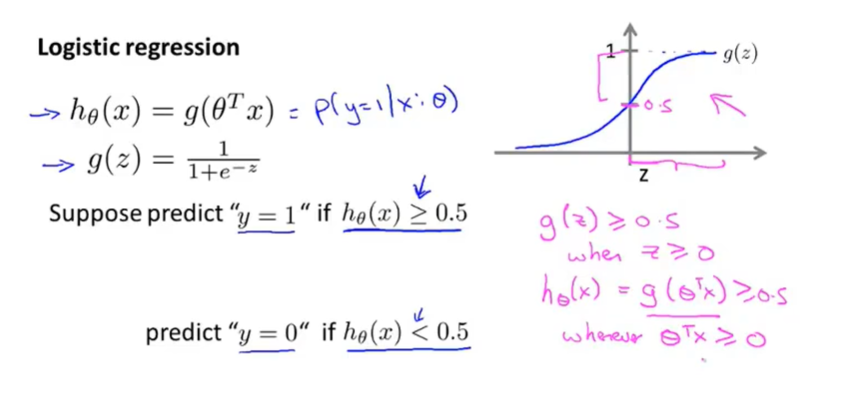
image.png

决策界限

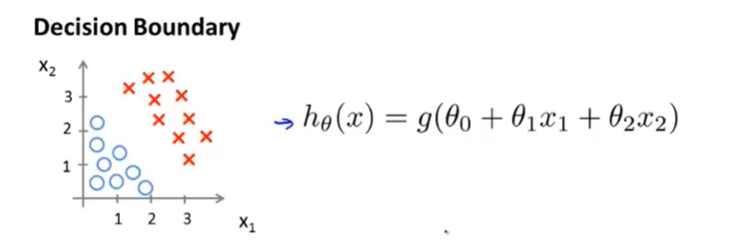
image.png
因此当【机器学习】分类问题 - 图11

image.png
假设已经算得模型参数的大小为
θ = [-3,1,1]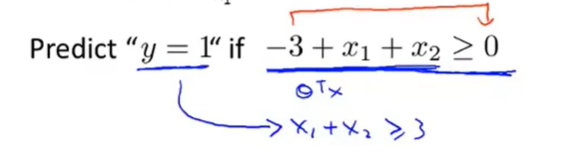
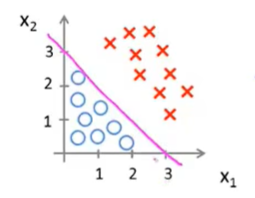
image.png
image.png
所以决策边界是预测函数【机器学习】分类问题 - 图15的一个属性

一个更复杂的例子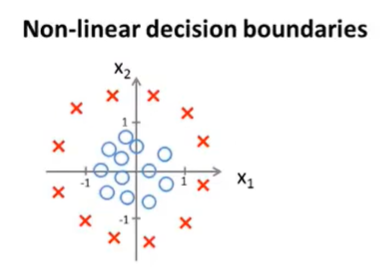
image.png
对logistics添加高阶特征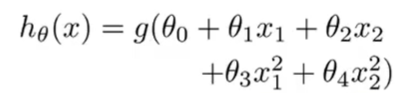
image.png
假设已经算得模型参数的大小为
θ = [-1，0，0，1，1]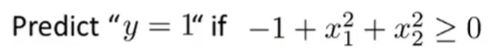
image.png
添加高阶的特征可以得到更复杂的边界
决策边界是预测函数和模型参数的属性，而不是数据集的属性。数据集仅决定了模型参数的数值大小

代价函数

优化目标/代价函数
image.png
回顾线性回归问题的代价函数
Cost function
Linear regression:【机器学习】分类问题 - 图20
如果同样用于logistics回归
即将【机器学习】分类问题 - 图21带入
这个代价函数会变为非凸函数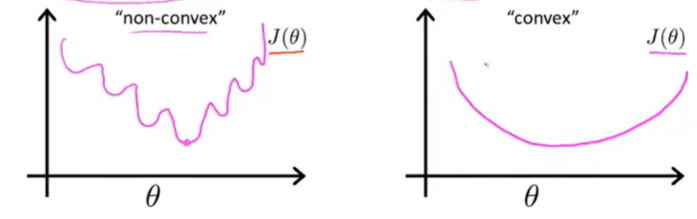
image.png
导致这个问题的主要原因是【机器学习】分类问题 - 图23的非线性
因此需要另外找一个合适的代价函数为凸函数，使得梯度下降法可以被使用，找到全局最小值
这个适用于logistics回归的代价函数如下
image.png
代价函数也是惩罚函数，惩罚标准是假设函数 【机器学习】分类问题 - 图25 和真实值 y 的偏差大小
image.png

巧妙地利用了这个函数的特征
当真实值是1，假设值也是1，代价/乘法是0
当真实值是1，假设值却是0，代价/乘法趋于无穷

简化函数

image.png
y 的取值有限，为了避免将 y 分情况处理，可以简化代价函数，合并等式

【机器学习】分类问题 - 图28
因此化简后的代价函数为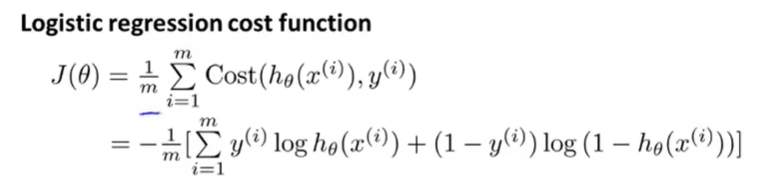
image.png
来源于统计学极大似然估计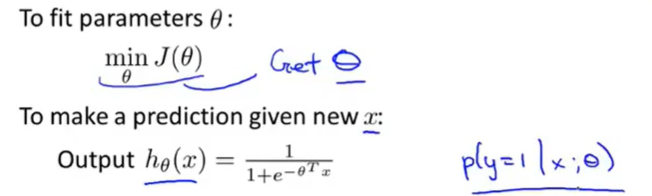
image.png

梯度下降

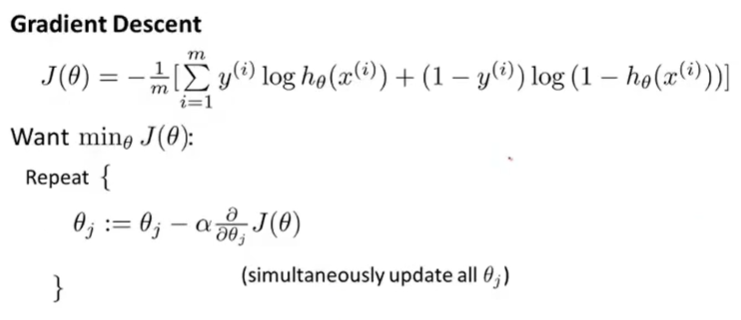
image.png
带入后和线性回归的梯度下降一模一样，但是假设函数不同