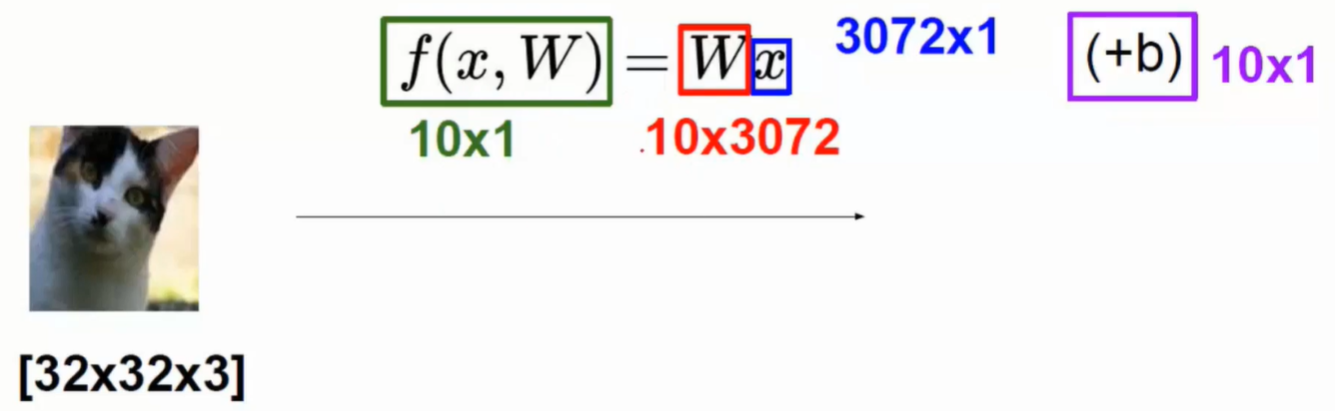
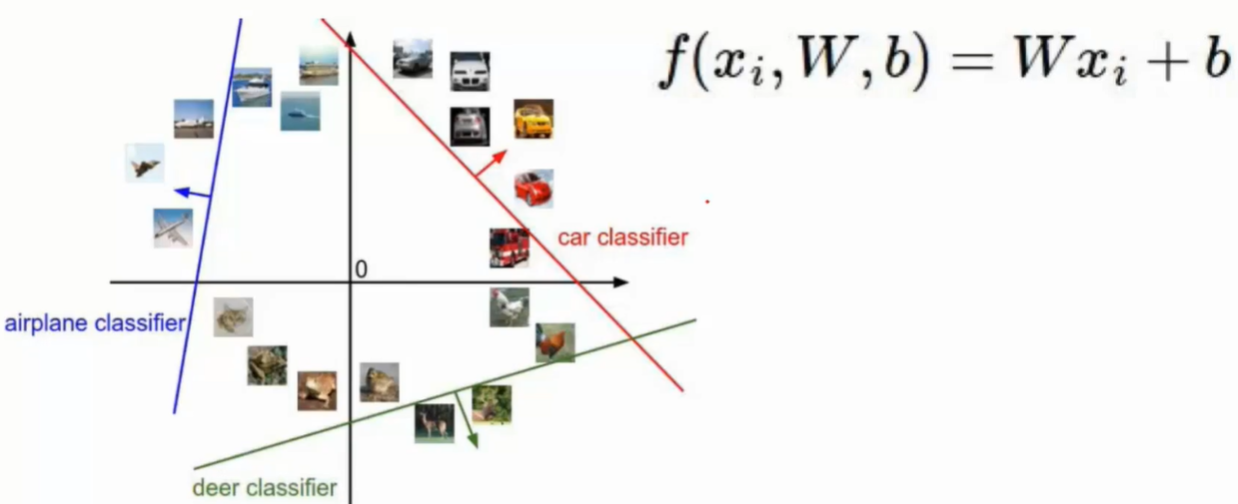
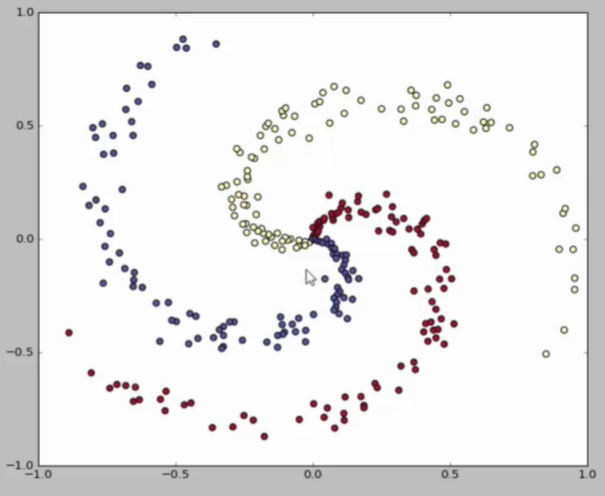
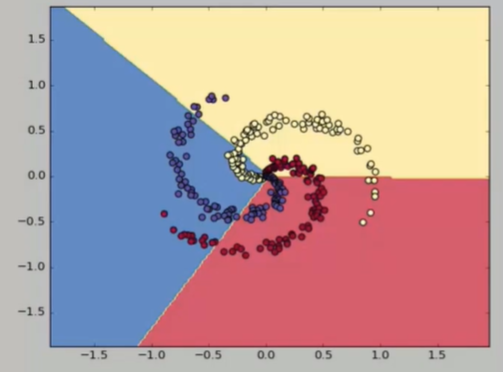
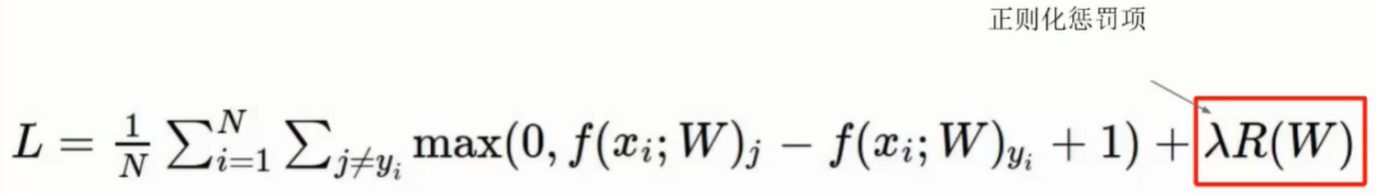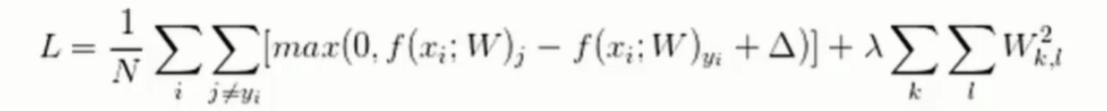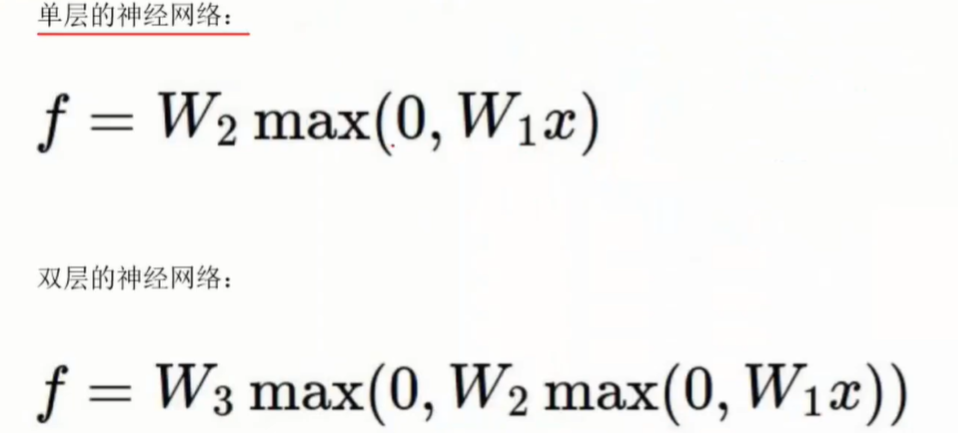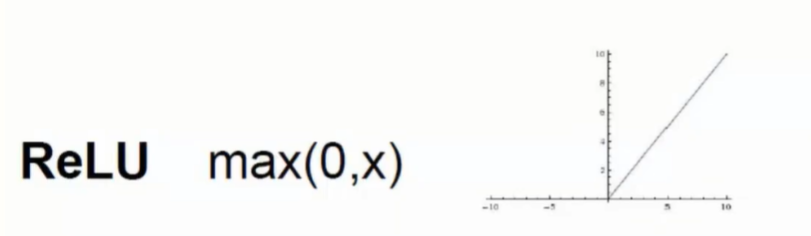线性分类

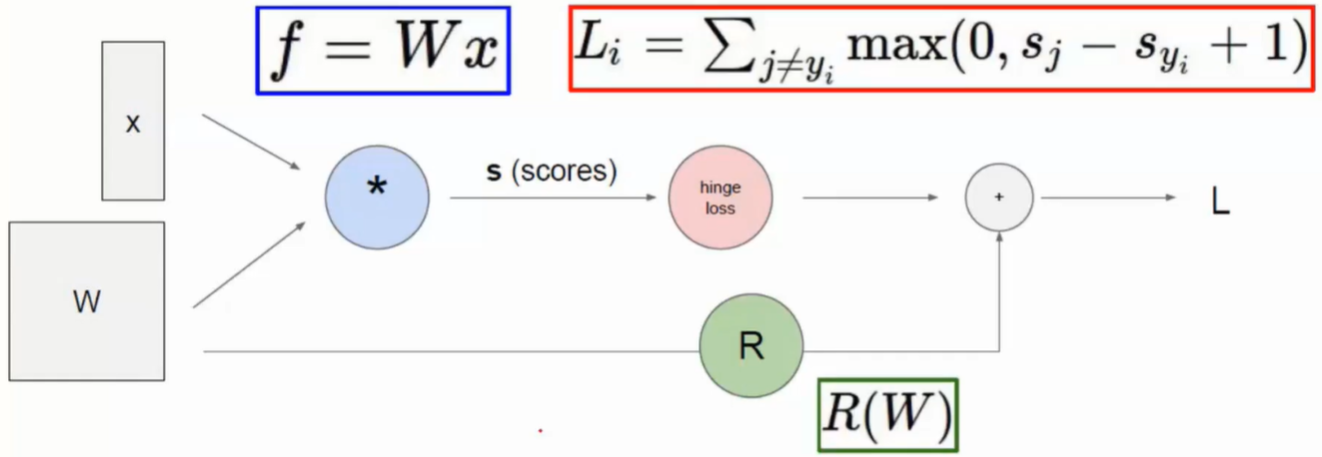
image.png
image.png
image.png
image.png

损失函数

  • 评判模型判断错误的损失，即评估预测效果，偏差程度
  • 举简单例子

image.png

  • 其中+1是定义了一个可以容忍的程度，认为最小的容忍程度是1

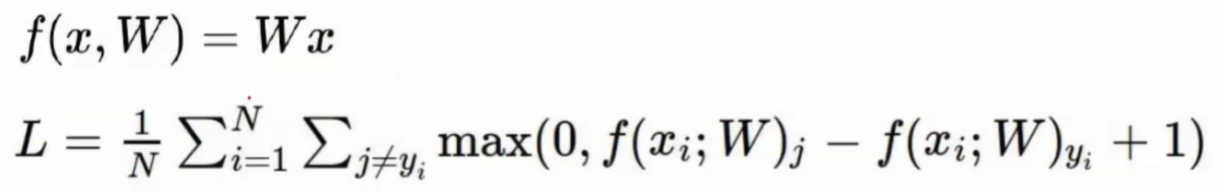
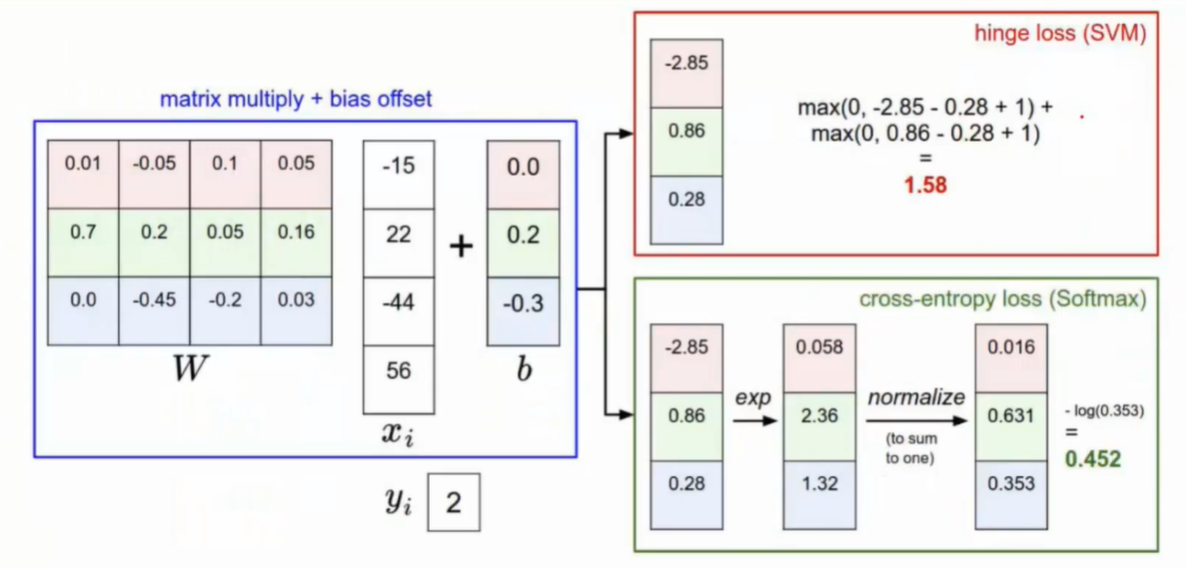
image.png
image.png

  • 大量测试，求和操作，除以N求平均每个样本的偏差

    正则化

    image.png
    image.png

    Softmax分类器

    image.png

  • 概率值比得分值更直观

  • 通过softmax使得分值可以转换为概率值
  • 使用了sigmoid函数

image.png
image.png

  • 实例

image.png

  • 先进行e的次幂操作，然后归一化，再用－log函数将它的正确概率值转换损失函数
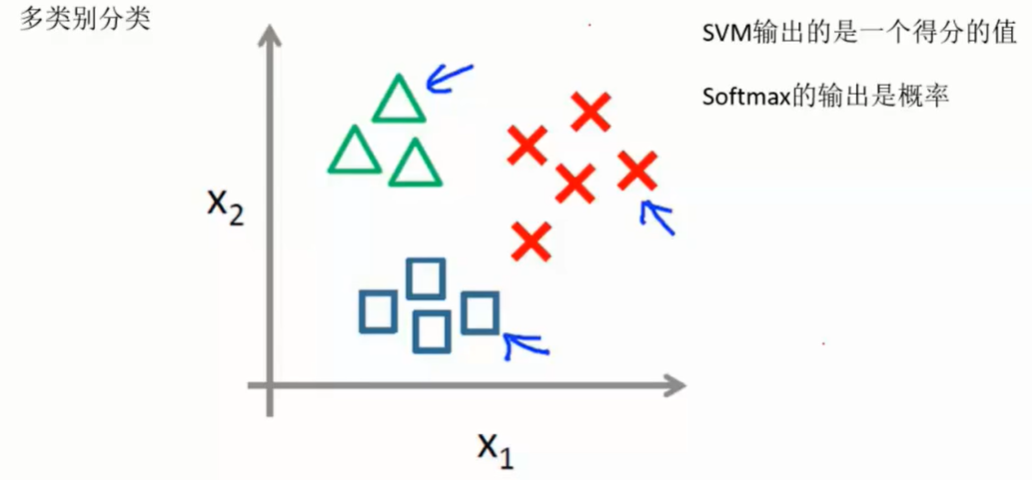
  • 结果对比

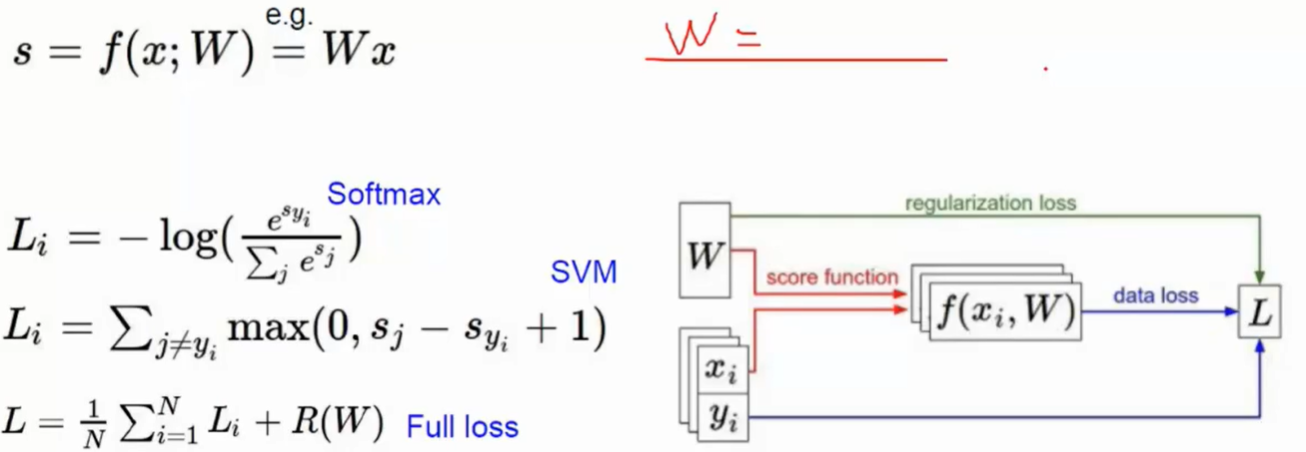
image.png

  • 通过softmax放大误差值，使得损失函数更为精细

    最优化

  • 梯度下降

image.png

  • 如果使用简单的想法

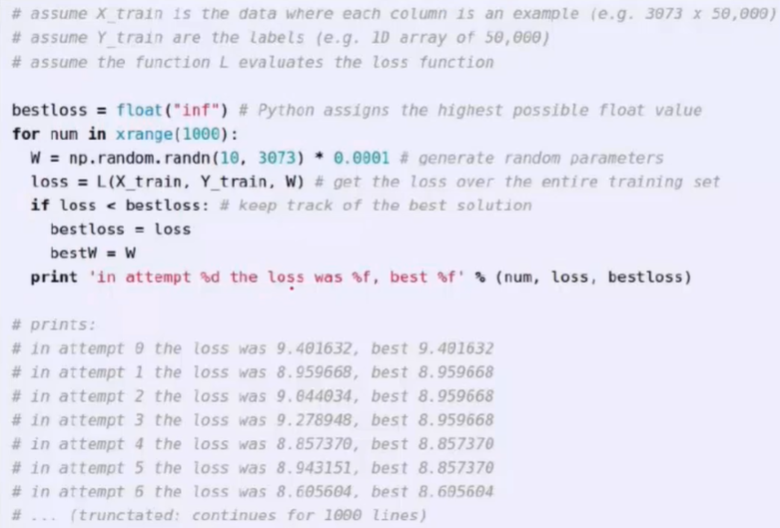
image.png

  • 计算结果

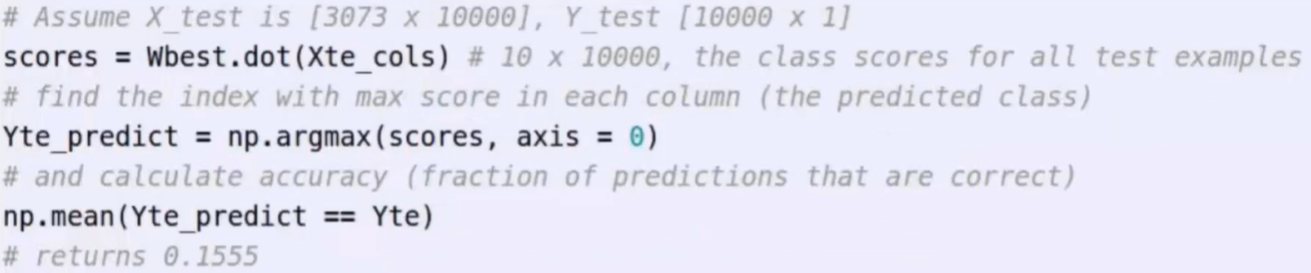
image.png

  • 找到最低点

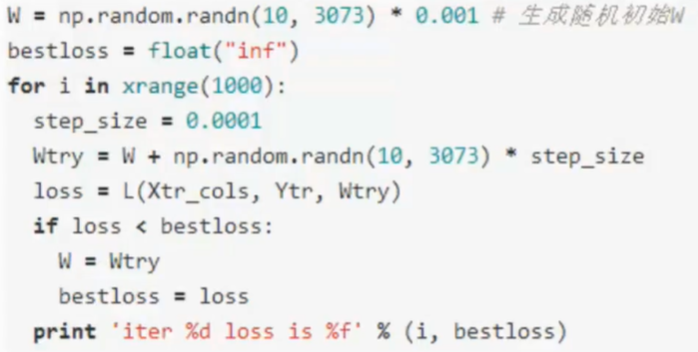
image.png

  • 跟随梯度

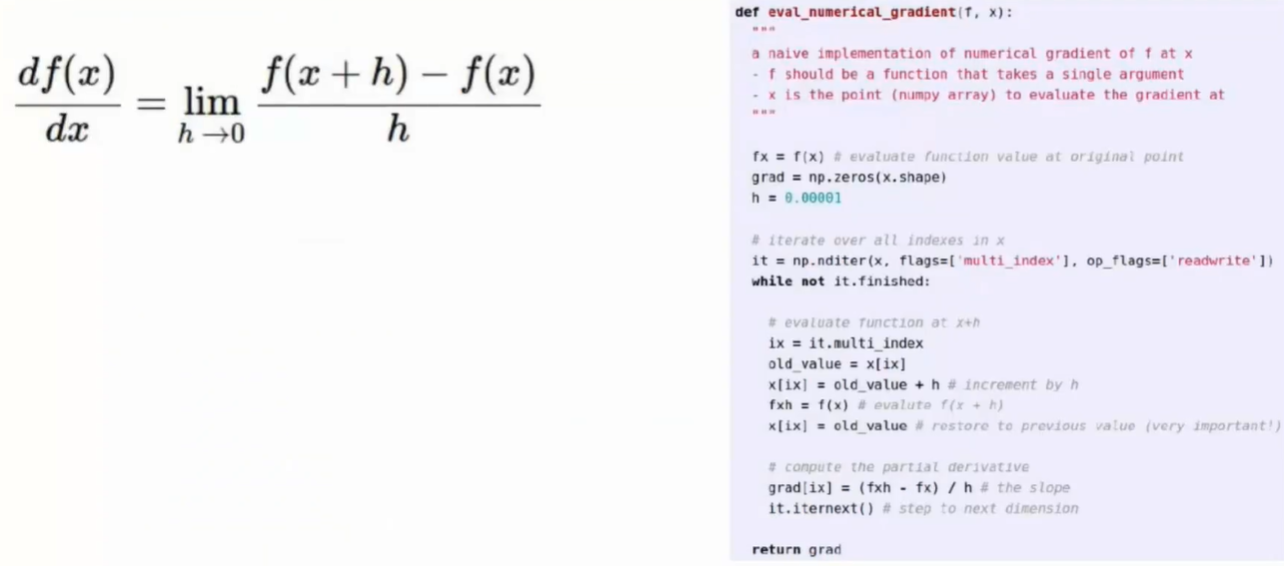
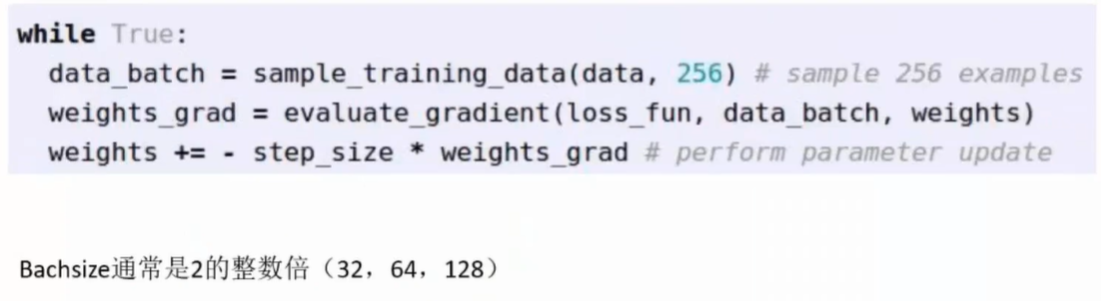
image.png

  • 小批量梯度下降

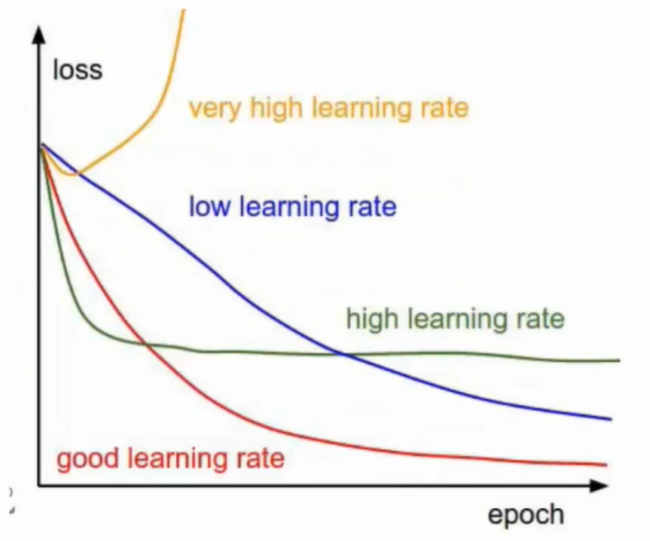
image.png

学习率

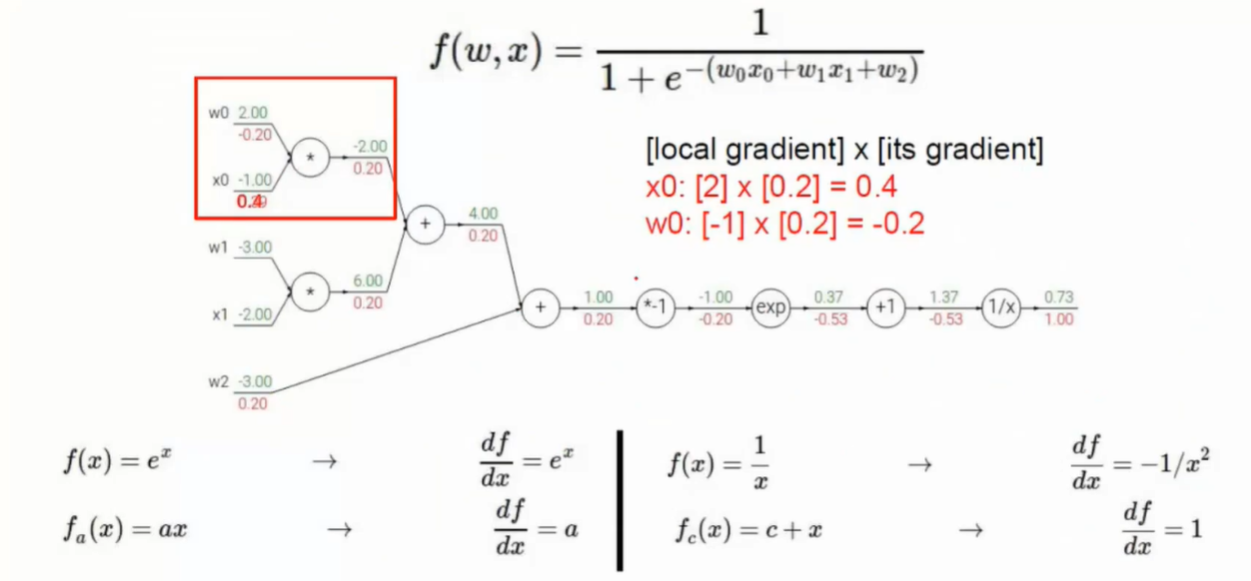
image.png

反向传播

image.png

  • 前向传播得到损失函数loss值
  • 反向传播使用得到的损失函数反推权重参数w

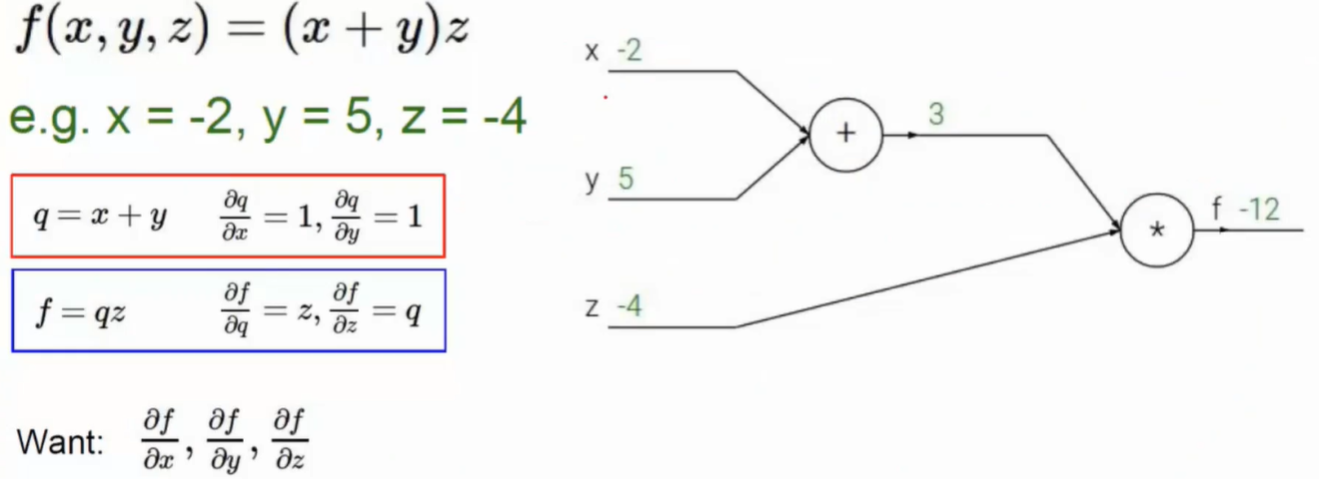
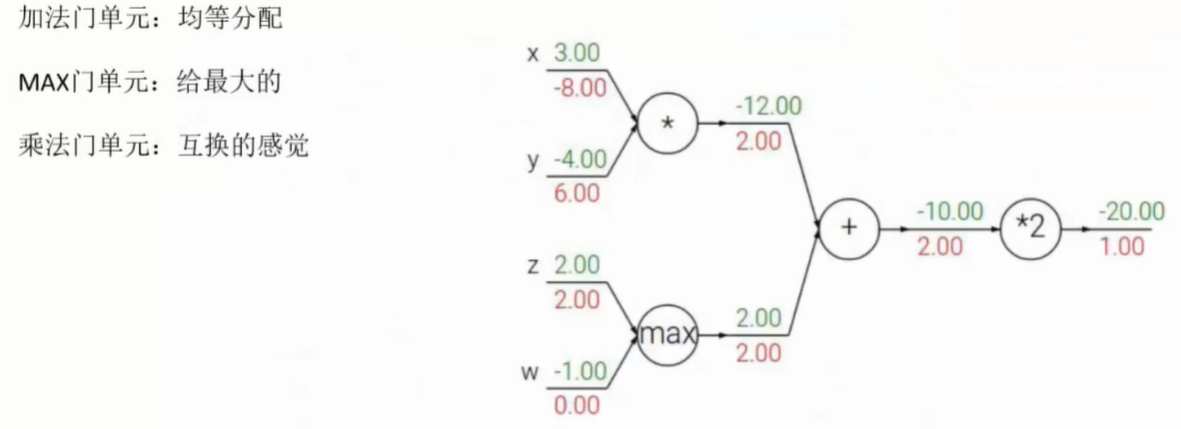
image.png

  • 链式法则

【Python】DL_神经网络 - 图24

  • 反向传播中计算每一个权重参数对最终的结果做出了多大的贡献

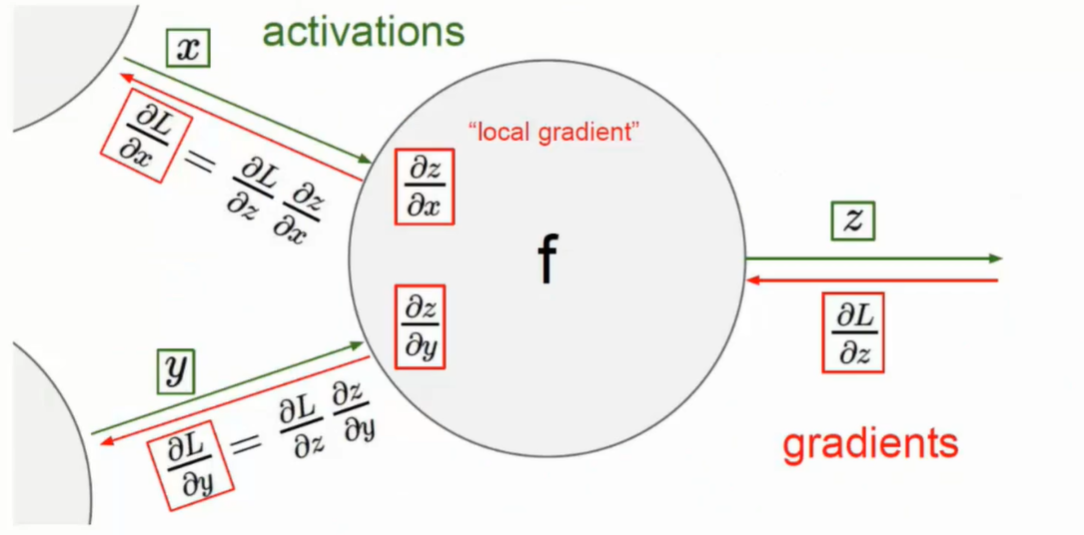
image.png

  • 影响不可跨级，一定是一级一级向下传递

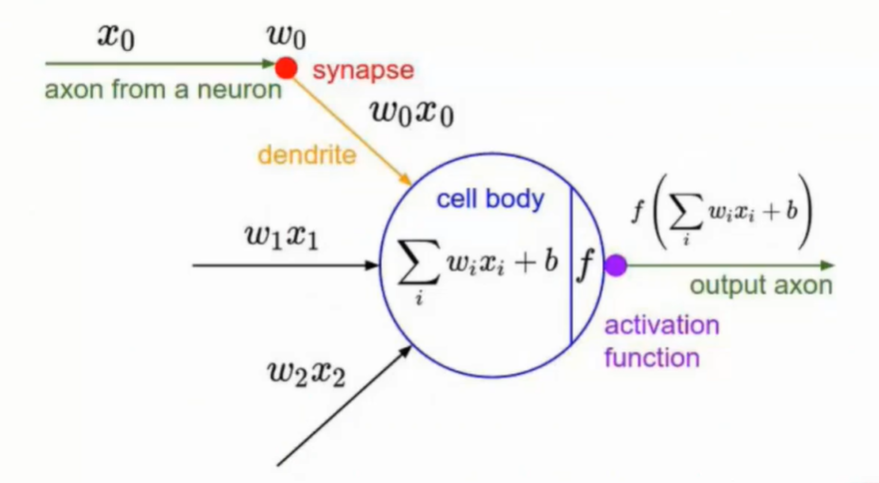
image.png
image.png
image.png

网络架构

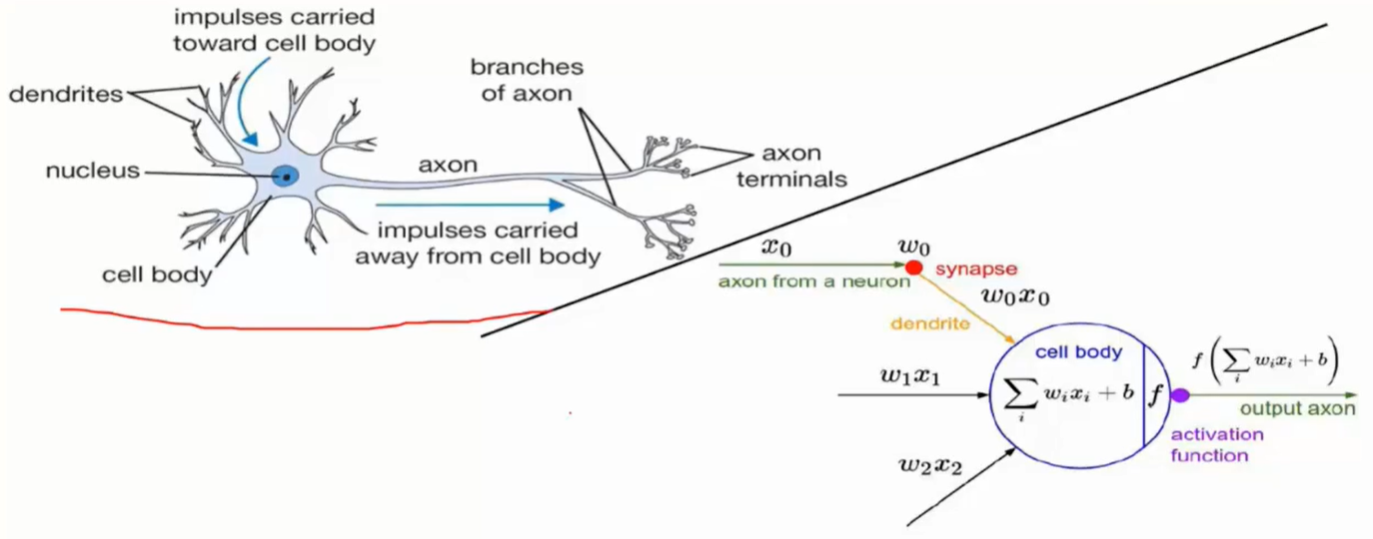
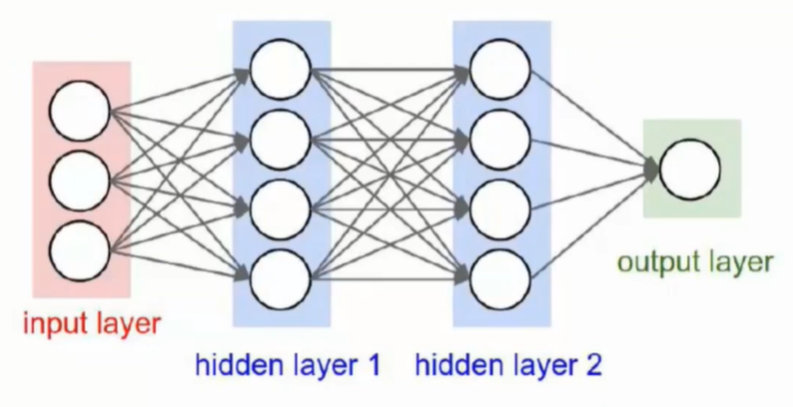
image.png
image.png

  • 层之间的连线即为权重参数
  • 权重参数的组合作用得到最终结果

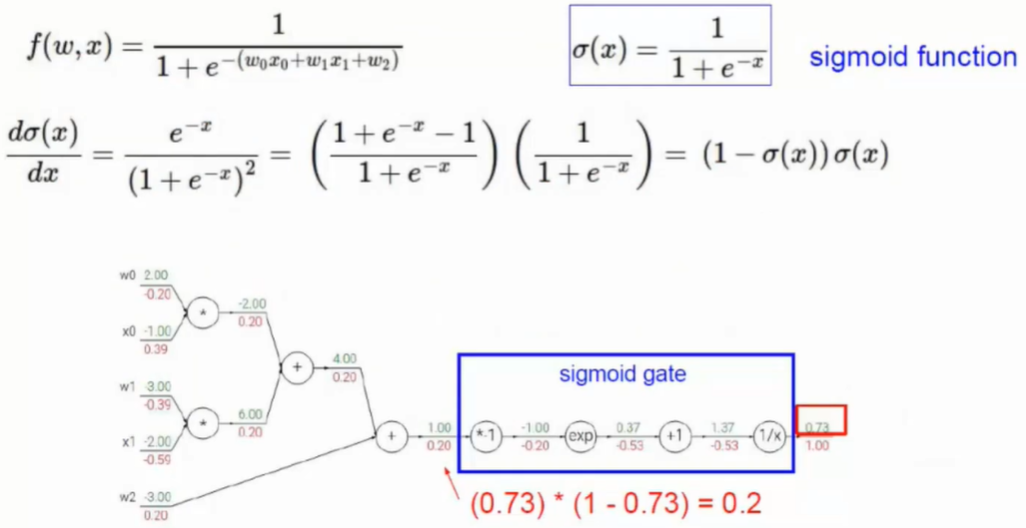
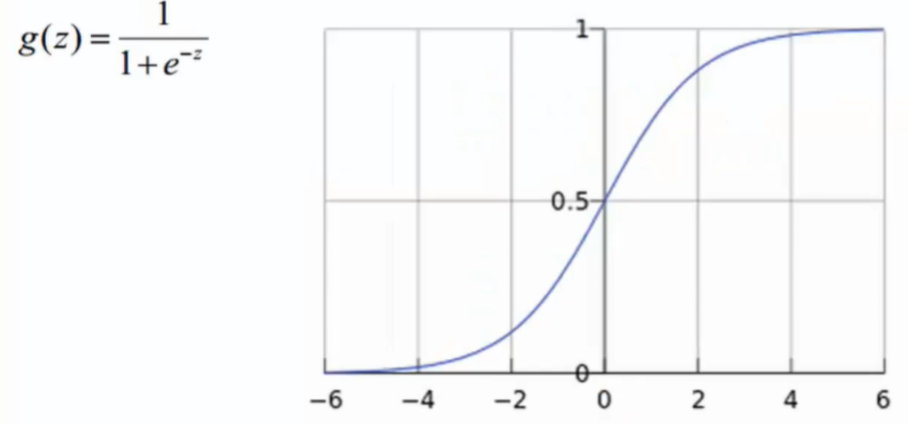
image.png
image.png

激活函数

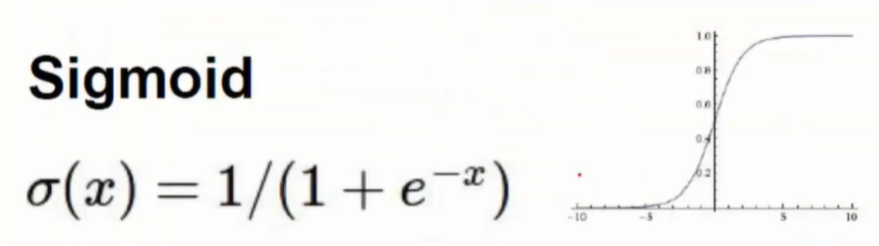
image.png

  • 在中间层每次不仅只有权重参数在发挥作用，还有像Sigmode这样的激活函数作用
  • 使用Sigmod作为激活函数会存在问题
  • 反向传播中需要对权重参数的导数累乘
  • 但是Sigmoid函数在x较大或较小的数值时导数约为0
  • 这样在传递的过程中会导致出现梯度消失的现象，就导致没有办法迭代
  • 当层数较多就容易导致梯度消失
  • 因此使用ReLU函数取代Sigmoid函数

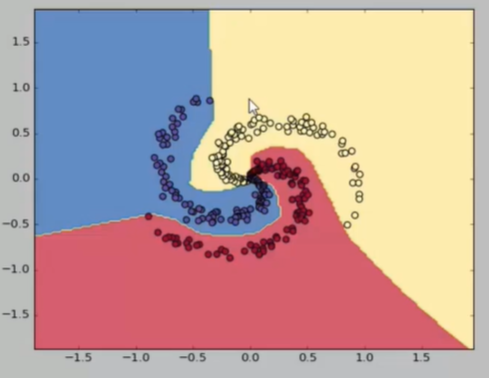
image.png

可视化演示

ConvnetJS demo

正则化项

  • 过拟合是神经网络的最大问题
  • 可通过正则化项抑制过拟合

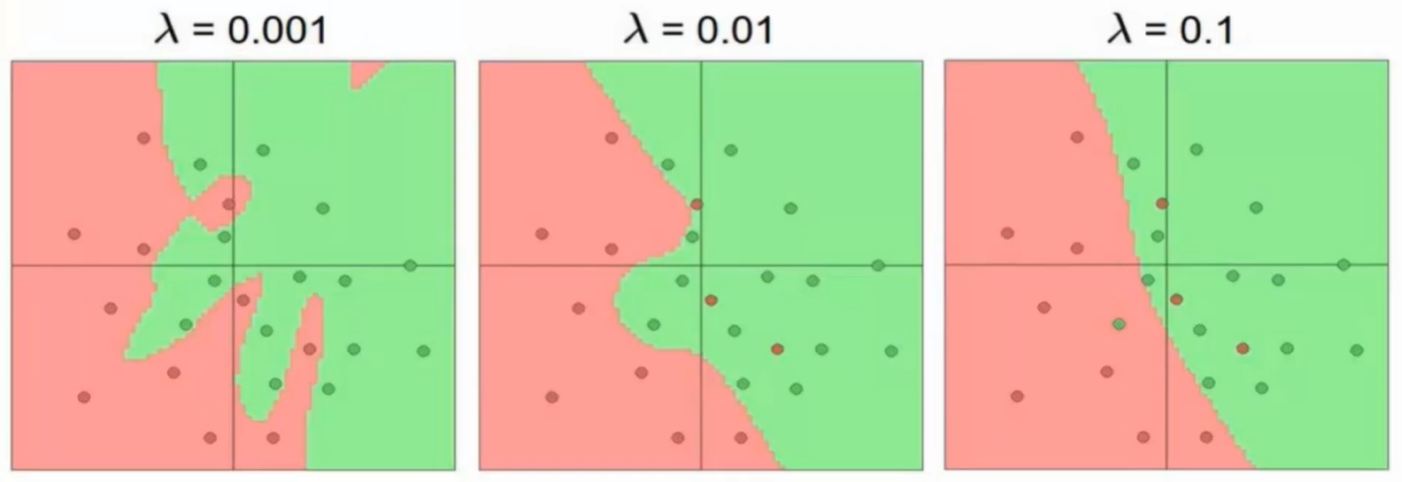
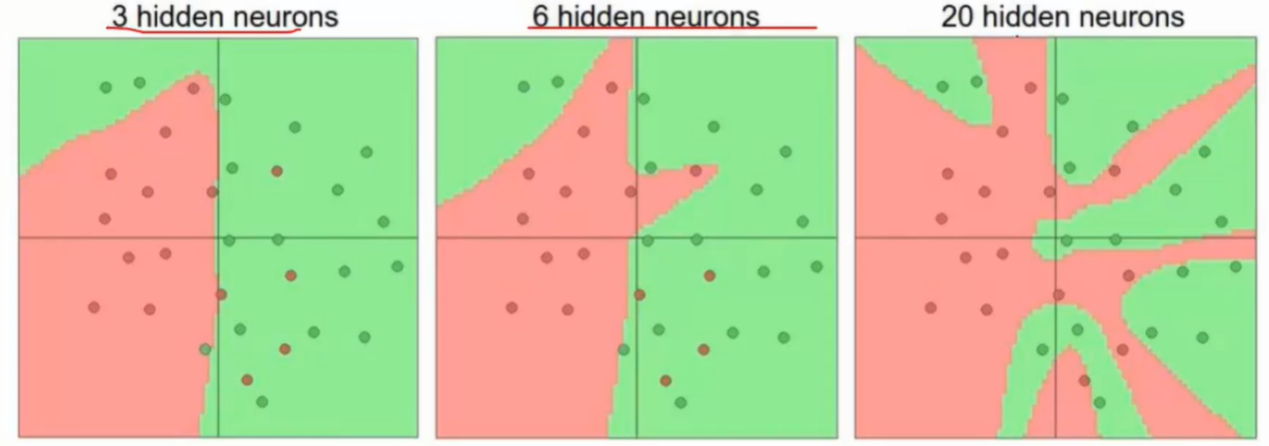
image.png
image.png

  • 越多的神经元，就越能够表达复杂的模型

    完整的层结构

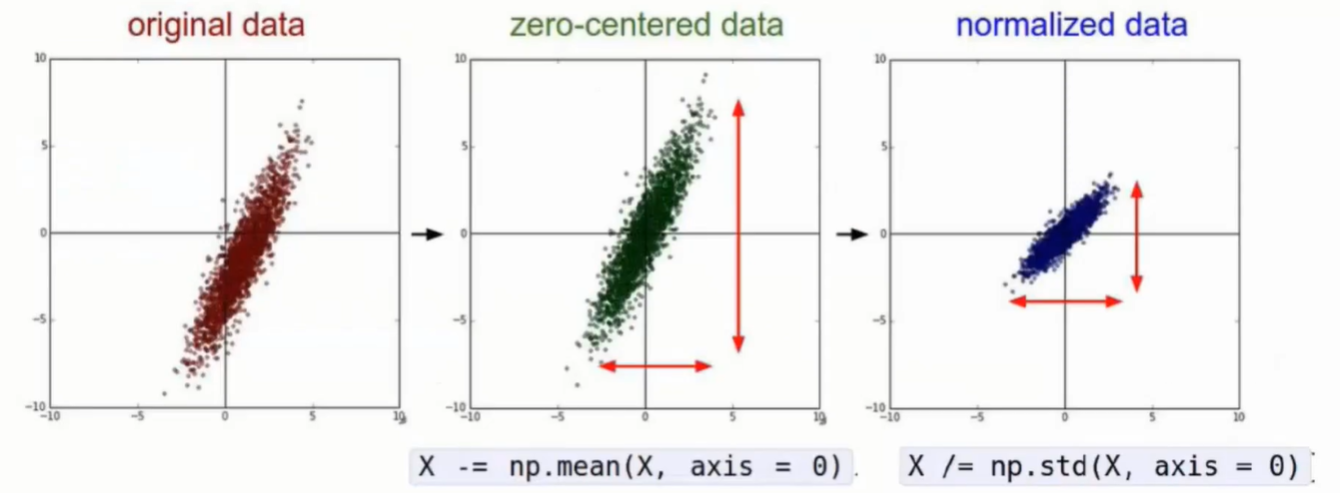
    image.png

    数据预处理

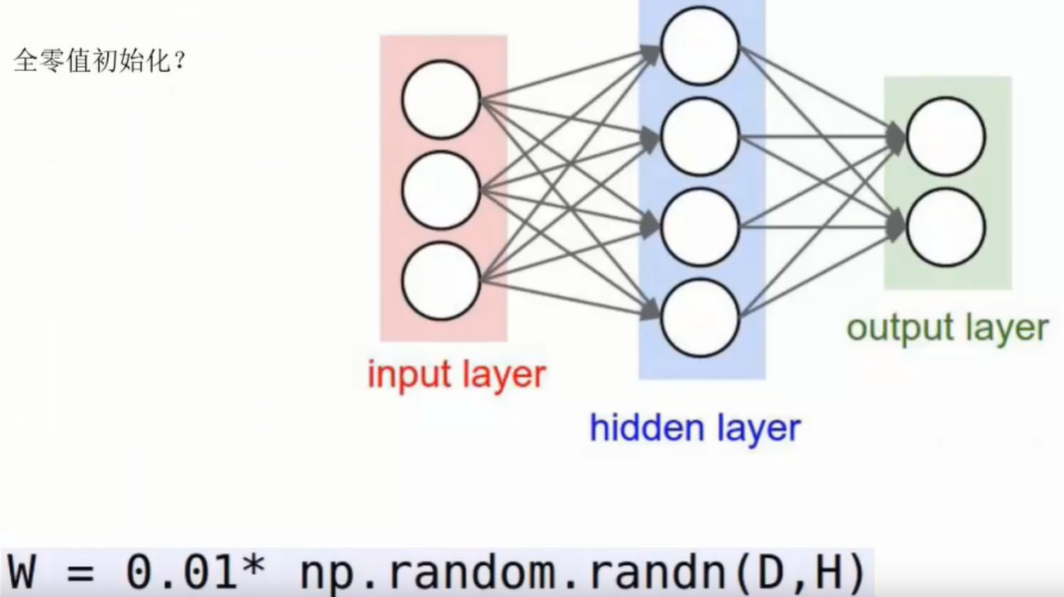
    image.png

    权重初始化

    image.png

  • 开始时对权重参数取随机值，不能取零值均值

  • 旁值b可以用0或1初始化

    DROP-OUT

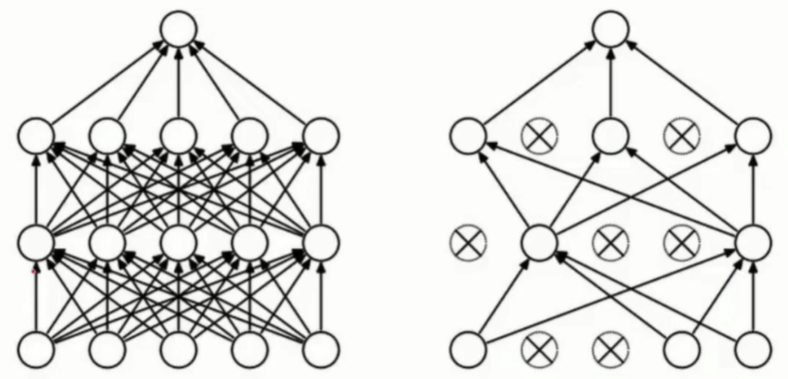
    image.png

  • 全连接操作运行慢且复杂

  • Drop-out策略，每次传播随机选择一定数量的元计算，可指定Drop-out率
  • 可削减神经网络规模

  • 降低过拟合的风险

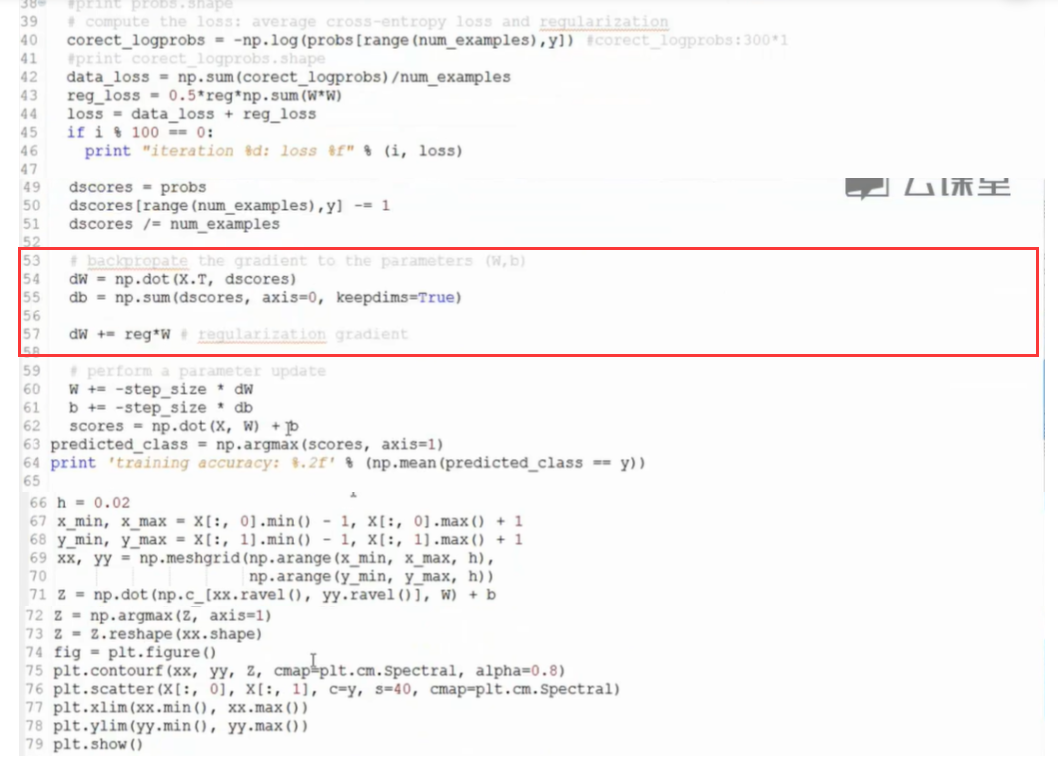
    Python实现

  • 分类任务

    线性回归

    image.png
    image.png
    image.png
    image.png
    image.png
    image.png
    image.png
    image.png
    image.png

    神经网络

  • 两层神经网络

image.png
替换上图片部分区域
image.png
image.png