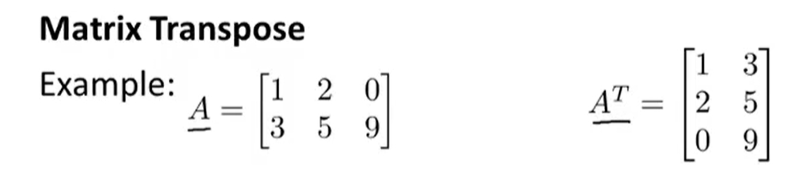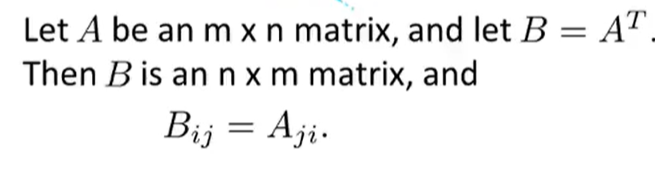定义

Matrix: Rectangular array of numbers
Dimension of matrix: number of rows * number of columns

通常大写字母表示矩阵，小写字母表示数字

Vecor: An n*1 matrix

矩阵加法/减法

Matric addition
对应项相加
只有维度相同的矩阵可以相加减

标量乘法/除法

Scalar Multiplication
n * A = nA
矩阵的每一项乘上标量
支持交换律
除法即为乘上标量的倒数

向量乘法

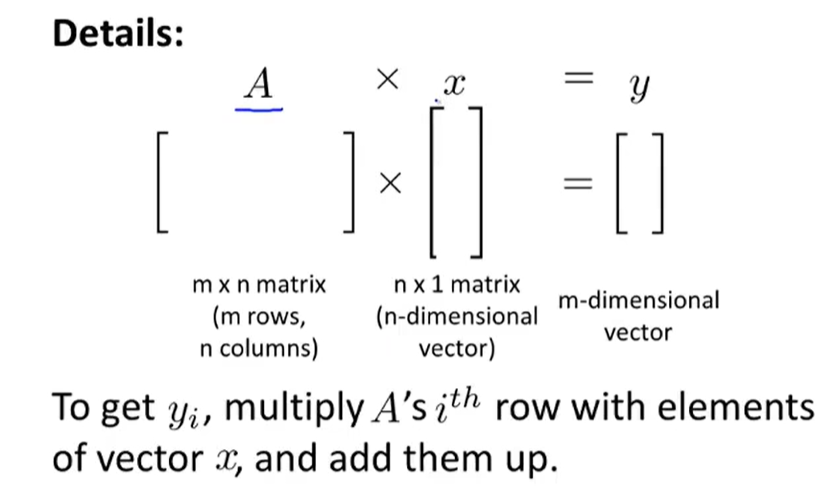
Matrix Vector
维度需要满足 mn × n1 = m1
计算过程是 的行 分别和 的列 作用的结果

可以方便表示和计算，比循环计算效率更高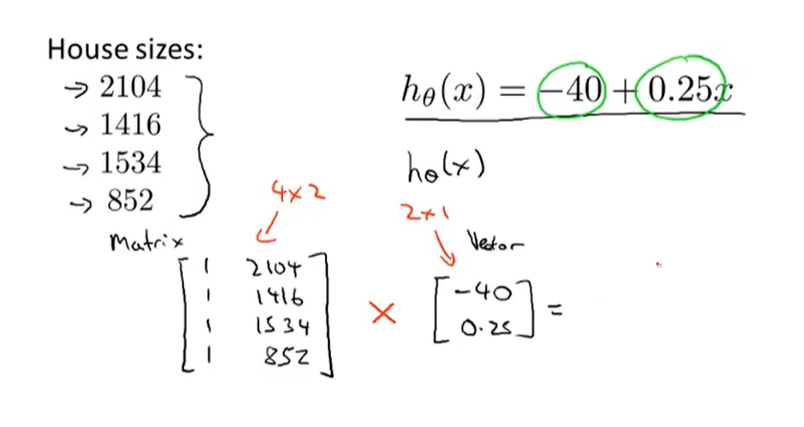

矩阵乘法

Matrix Matrix
维度需要满足 mn × nk = mk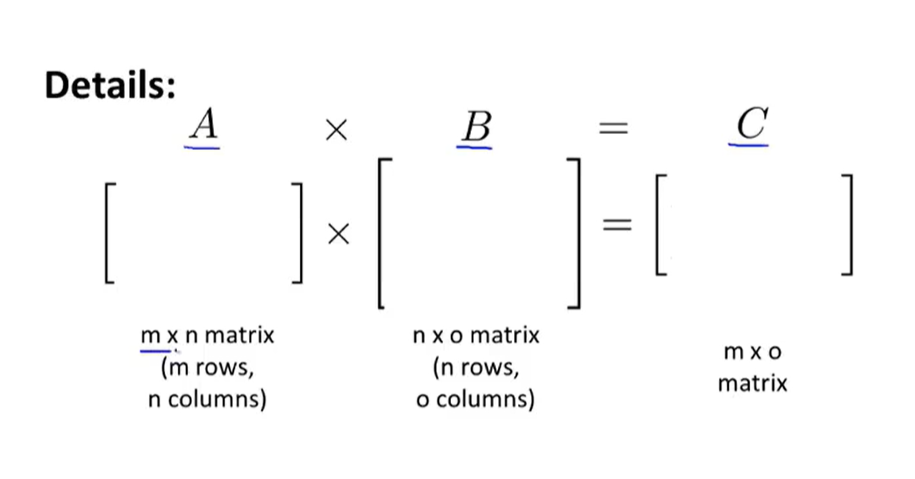



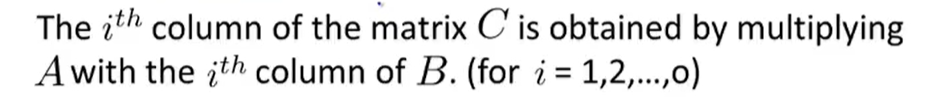
线性代数库

矩阵乘法特性

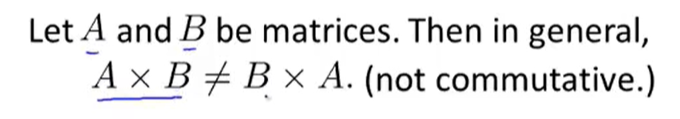
不满足交换律
甚至会改变维度
但是满足结合律

Identity Matrix
单位矩阵
（对角线上为1，其它为0）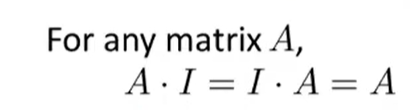

需要确保维度正确

矩阵的逆

类比于实数的倒数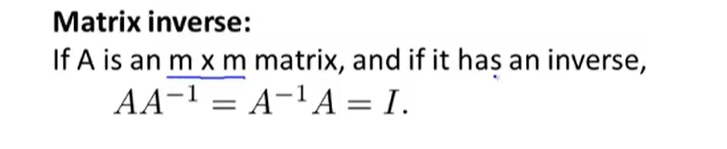

只有方阵有逆矩阵
并不是所有的阵有逆矩阵（奇异矩阵）
需要判决是否存在逆矩阵

矩阵的转置