引例

image.png
image.png

  • 在这个例子中，算法预测结果有99%正确的，1%是错误的
  • 看似这个算法的预测结果是比较准确的
  • 但是在所有样本中只有0.5%的患者患了癌症
  • 如果不通过任何算法，直接判断样本没有患癌症，这样错误率也仅有0.5%
  • 这样看，预测结果的实际作用不大

  • 实际情况中的 0.5% 就属于偏斜类

    问题

  • 当使用分类算法时会遇到这样的问题

    • 如果使用分类误差或分类精确度作为评估度量会导致难以衡量算法是否得到了改进
    • 预测的准确度从99.2%提升到了99.5%，也不能说算法得到了提升吗
    • 因此需要一种评估度量值的办法

      解决

      查准率/召回率

      image.png

  • 通过这两个指标，可以有效的避免“如果不通过任何算法，直接判断样本没有患癌症，这样错误率也仅有0.5%”这类欺骗算法

  • 从而可以更真实地优化分类模型，避免了倾斜类地影响

    权衡

    需要保证查准率和召回率的相对平衡

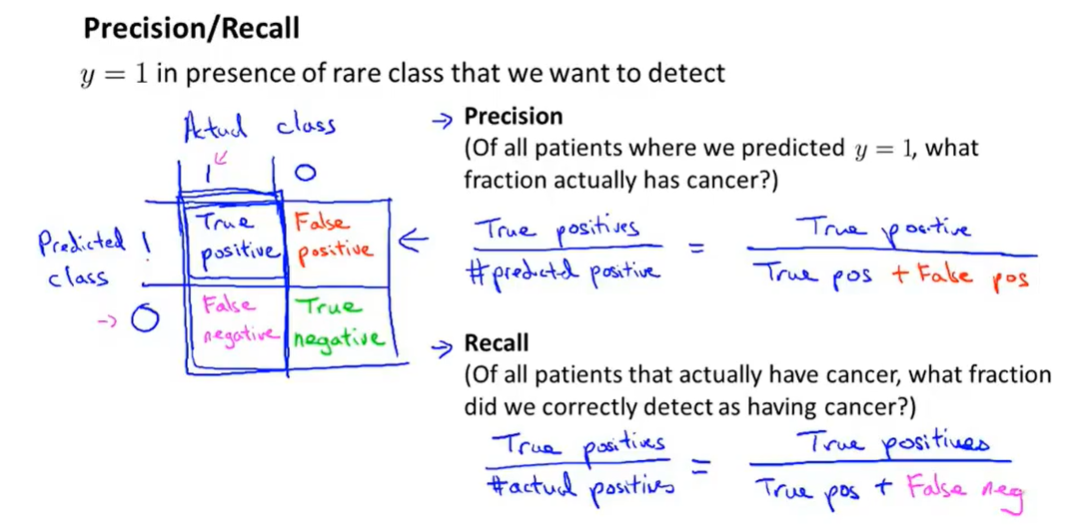
  • 查准率和召回率的定义

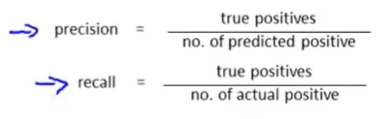
image.png

  • 逻辑回归定义

image.png

  • 修改模型（避免误判）

image.png
修改预测函数的输出值的概率为较大数值，使得判定结果为 1 更加谨慎
这是一个高查准率的模型，而召回率会偏低（预测为1更确定确实是1，但实际中的1被预测出来的比较少）

  • 修改模型（避免漏判）

image.png
修改预测函数的输出值的概率为较小数值，使得判定结果为 1 更加容易
这是一个高召回率的模型，而查准率会偏低

综上可以调整h(x)的临界值，来调整召回率和查准率以适应不同的需求

选取

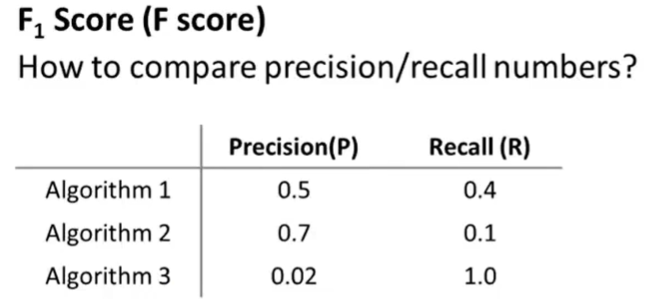
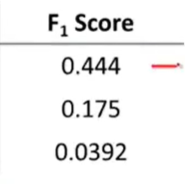
image.pngimage.png
image.png

  • F值是结合查准率和召回率一个有效的选取参数（两者必须同时大才可）
  • 可通过尝试不同的预测函数的临界值，在验证集中计算F参数，自动选取高召回率高查准率的临界值