1. 题目描述

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

进阶：你可以实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案吗？

示例 1：

  1. 输入：nums = [1,2,0]
  2. 输出：3

示例 2：

  1. 输入：nums = [3,4,-1,1]
  2. 输出：2

示例 3：

  1. 输入：nums = [7,8,9,11,12]
  2. 输出：1

提示：

  • 0 <= nums.length <= 300
  • -2 <= nums[i] <= 2 - 1

    2. 解题思路

    对于这道题目，要求在O(n)的时间复杂度内完成，那我们就要在不影响原数组的基础上进行操作。

我们假设缺失的第一个正数是n，那么如果将这个数组按照从小到大排序完之后，1~n-1都应该排在n前面，比n大的数不会影响最后的结果。所以nums数组的长度最小就是n-1，即 n >= nums.length；我们可以遍历数组，对于大于1，并且小于nums.length - 1 的元素不用进行交换。在这个区间的元素交换到nums[i] - 1 的位置。简单来说就是将元素换到数组中第元素的值的位置。这样，最后如果当前数组中nums[i] != i + 1，就说明这个元素是缺失的元素。

示例2交换后的顺序如下：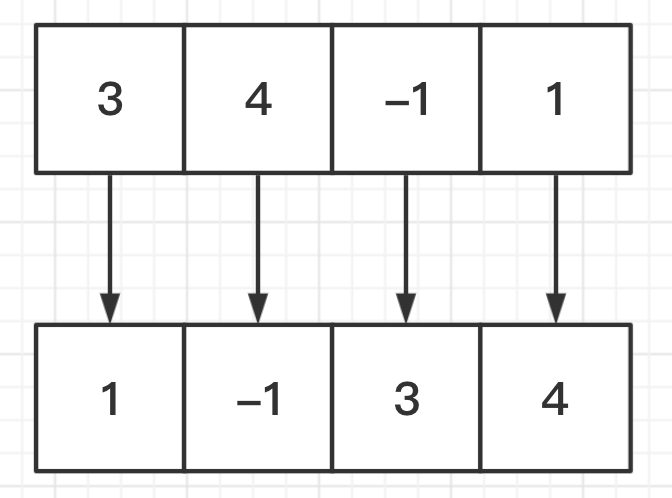
image.png
复杂度分析：

  • 时间复杂度：O(n)，其中n是数组的长度，需要遍历两次数组，第一次进行交换。第二次查找结果，时间复杂度为O(2n)；

  • 空间复杂度：O(1)，这里不需要额外的空间储存变量，所以空间复杂度为O(1)。

    3. 代码实现

    1. /**
    2. * @param {number[]} nums
    3. * @return {number}
    4. */
    5. var firstMissingPositive = function(nums) {
    6.   const len = nums.length
    7.   if(!len){
    8.       return 1
    9.   }
    10.   for(let i = 0; i < len; i++){
    11.       while(nums[i] >= 1 && nums[i] <= len && nums[nums[i] - 1] !== nums[i]){
    12.           const temp = nums[nums[i] - 1]
    13.           nums[nums[i] - 1] = nums[i]
    14.           nums[i] = temp
    15.       }
    16.   }
    18.   for(let i = 0; i < len; i++){
    19.       if(nums[i] !== i + 1){
    20.           return i + 1
    21.       }
    22.   }
    23.   return len + 1
    24. };

    4. 提交结果

    image.png