222. 完全二叉树的节点个数

1. 题目描述

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2 个节点。

示例 1：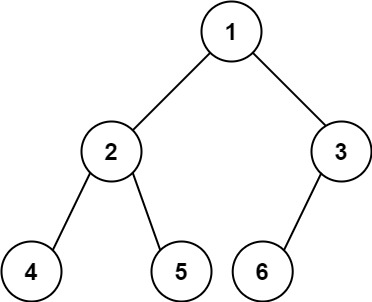

输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示：

• 树中节点的数目范围是[0, 5 * 10]
• 0 <= Node.val <= 5 * 10

• 题目数据保证输入的树是 完全二叉树

  
  进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

  2. 解题思路

  对于这道题目，我们可以使用深度优先遍历或者广度优先遍历来计算二叉树的节点数。

1）深度优先遍历：深度优先遍历就很简单了，题中传入的是二叉树，需要返回的是二叉树，所以可以直接进行递归计算二叉树的节点数：

• 如果子树为空节点数为 0
• 如果子树存在左子树或右子树则节点数+1，继续递归分别求左子树节点数和右子树节点数

复杂度分析：

• 时间复杂度：O(n)，其中n是二叉树的节点数，我们需要遍历一遍整个二叉树；
• 空间复杂度：O(h)，其中h是二叉树的高度，递归的时间复杂度为O(h)。

2）广度优先遍历：**广度优先遍历往往是初始化一个对来保存当前层的节点，在对当前层的节点进行操作。对于这题目，我们只需要在节点进入队列的时候，结果加一即可。

复杂度分析：

• 时间复杂度：O(n)，其中n是二叉树的节点数，我们需要遍历一遍整个二叉树；
• 空间复杂度：O(n)，其中n是队列的长度，我们需要将每一层都放在队列中。

3）二分法
上面的两种方法的时间复杂度都是O(n)，下面用二分法来解决，时间复杂度会降低。

我们知道，对于一个完全二叉树，它的所有子树都是完全二叉树，有的子树是满二叉树，满二叉树的的节点个数计算公式如下：2-1，其中h为当前树的高度。

那什么情况下就是满二叉树呢，我们知道，二叉树中有个树的深度的概念，指的就是根节点到这个节点所经历的边的个数，所以我们只需要判断左右子树的高度手否相等来判断当前树是不是满二叉树。

如果不是满二叉树，那就是规模小一点的完全二叉树，就进行递归处理。

复杂度分析：

• 时间复杂度：每次递归调用对应了一层树高，调用logN次，每次调用计算完全二叉树的高度需要O(logN)，所以时间复杂度为O(logN)

• 空间复杂度：O(1)，我们只需要维护有限的额外空间。

  3. 代码实现

  广度优先遍历：

  /**
  * Definition for a binary tree node.
  * function TreeNode(val, left, right) {
  *     this.val = (val===undefined ? 0 : val)
  *     this.left = (left===undefined ? null : left)
  *     this.right = (right===undefined ? null : right)
  * }
  */
  /**
  * @param {TreeNode} root
  * @return {number}
  */
  var countNodes = function(root) {
    if(!root){
        return 0
    }
    let queue = [root]
    let res = 1
    while(queue.length){
        let node = queue.shift()
        if(node.left){
            queue.push(node.left)
            res++
        }
        if(node.right){
            queue.push(node.right)
            res++
        }
    }
    return res
  };

  深度优先遍历：

  /**
  * Definition for a binary tree node.
  * function TreeNode(val, left, right) {
  *     this.val = (val===undefined ? 0 : val)
  *     this.left = (left===undefined ? null : left)
  *     this.right = (right===undefined ? null : right)
  * }
  */
  /**
  * @param {TreeNode} root
  * @return {number}
  */
  var countNodes = function(root) {
    if(!root){
        return 0
    }
    return 1 + countNodes(root.left) + countNodes(root.right)
  }

  二分法：

  /**
  * Definition for a binary tree node.
  * function TreeNode(val, left, right) {
  *     this.val = (val===undefined ? 0 : val)
  *     this.left = (left===undefined ? null : left)
  *     this.right = (right===undefined ? null : right)
  * }
  */
  /**
  * @param {TreeNode} root
  * @return {number}
  */
  var countNodes = function(root) {
    if(!root){
        return 0
    }
    let leftHeight = 0, rightHeight = 0
    let leftNode = root, rightNode = root
    while(leftNode){
        leftHeight++
        leftNode = leftNode.left
    }
    while(rightNode){
        rightHeight++
        rightNode = rightNode.right
    }
    if(leftHeight === rightHeight){
        return 2 ** leftHeight - 1
    }
    return 1 + countNodes(root.left) + countNodes(root.right)
  };

  4. 提交结果

  广度优先遍历：
  
  深度优先遍历：
  
  二分法：