1. 题目描述

给定一个二叉树，确定它是否是一个完全二叉树。

百度百科中对完全二叉树的定义如下：**

若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。（注：第 h 层可能包含 1~ 2 个节点。）

示例 1：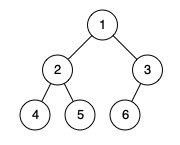
958. 二叉树的完全性检验 - 图1

  1. 输入：[1,2,3,4,5,6]
  2. 输出：true
  3. 解释：最后一层前的每一层都是满的（即，结点值为 {1} 和 {2,3} 的两层），且最后一层中的所有结点（{4,5,6}）都尽可能地向左。

示例 2：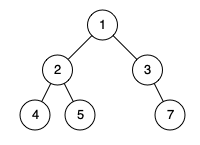
958. 二叉树的完全性检验 - 图2

  1. 输入：[1,2,3,4,5,null,7]
  2. 输出：false
  3. 解释：值为 7 的结点没有尽可能靠向左侧。

提示：

  1. 树中将会有 1 到 100 个结点。

    2. 解题思路

    对于这道题目，我们可以使用层序遍历来解决。在层序遍历的过程中，需要用一个index来维护节点的索引，如果一个节点的index，那它的左孩子的索引是index * 2，右孩子的索引是index * 2 + 1。

这里我们初始化一个队列，用来存储当前节点node和当前节点的索引值index。使用一个count来记录当前已经遍历到第几个节点。如果当前节点的索引值index和count + 1相等，那么说明当前节点的位置时正确的，就继续遍历，如果不相等，说明中间缺少了节点，直接返回false，结束遍历。

复杂度分析：

  • 时间复杂度：O(n)，这里最坏的情况就是我们需要遍历整棵二叉树，所以时间复杂度为O(n)，其中n是二叉树的节点的数量；

  • 空间复杂度：O(1)，我们需要初始化一个队列来保存当前遍历的节点，这个队列是一个常数空间，所以空间复杂度为O(1)。

    3. 代码实现

    1. /**
    2. * Definition for a binary tree node.
    3. * function TreeNode(val, left, right) {
    4. *     this.val = (val===undefined ? 0 : val)
    5. *     this.left = (left===undefined ? null : left)
    6. *     this.right = (right===undefined ? null : right)
    7. * }
    8. */
    9. /**
    10. * @param {TreeNode} root
    11. * @return {boolean}
    12. */
    13. var isCompleteTree = function(root) {
    14.   if(!root){
    15.       return true
    16.   }
    17.   let count = 0
    18.   const queue = [{ node: root, index: 1 }]
    20.   while(queue.length){
    21.       const temp = queue.shift()
    23.       const node = temp.node 
    24.       const index = temp.index
    25.       // 判断当前节点是否是正确的顺序值
    26.       if(index !== ++count){
    27.           return false
    28.       }
    29.       // 遍历当前节点的左右子树
    30.       node.left && queue.push({node: node.left, index: index * 2})
    31.       node.right && queue.push({node: node.right, index: index * 2 + 1})
    32.   }
    33.   return true
    34. };

    4. 提交结果

    image.png