说了半天，我们如何在内存中生成一棵二叉链表的二叉树呢？树都没有，哪来遍历。所以我们还得来谈谈关于二叉树建立的问题。

    如果我们要在内存中建立一个如图6-9-1左图这样的树，为了能让每个结点确认是否有左右孩子，我们对它进行了扩展，变成图6-9-1右图的样子，也就是将二叉树中每个结点的空指针引出一个虚结点，其值为一特定值，比如“#”。我们称这种处理后的二叉树为原二叉树的扩展二叉树。扩展二叉树就可以做到一个遍历序列确定一棵二叉树了。比如图6-9-1的前序遍历序列就为AB#D##C##。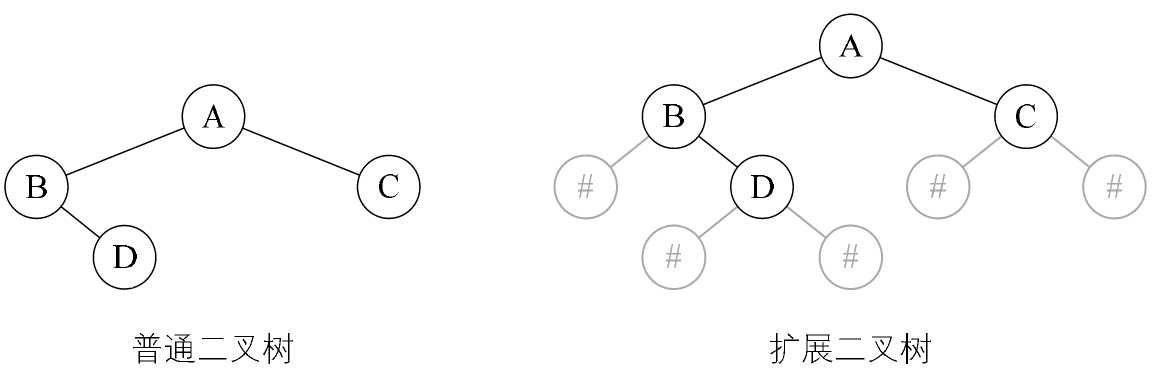
    image.png
    有了这样的准备，我们就可以来看看如何生成一棵二叉树了。假设二叉树的结点均为一个字符，我们把刚才前序遍历序列AB#D##C##用键盘挨个输入。实现的算法如下：

    1. /* 按前序输入二叉树中结点的值（一个字符） */
    2. /* #表示空树，构造二叉链表表示二叉树T */
    3. void CreateBiTree(BiTree *T){
    5.     TElemType ch;
    7.     scanf("%c", &ch);
    9.     if (ch == '#')
    10.         *T = NULL;
    11.     else{
    13.         *T = (BiTree)malloc(sizeof(BiTNode));
    15.         if (!*T)
    16.             exit(OVERFLOW);
    18.         /* 生成根结点 */
    19.         (*T)->data = ch;
    21.         /* 构造左子树 */
    22.         CreateBiTree(&(*T)->lchild);
    24.         /* 构造右子树 */
    25.         CreateBiTree(&(*T)->rchild);
    27.     } 
    29. }

    其实建立二叉树，也是利用了递归的原理。只不过在原来应该是打印结点的地方，改成了生成结点、给结点赋值的操作而已。所以大家理解了前面的遍历的话，对于这段代码就不难理解了。