2-3树是这样的一棵多路查找树：其中的每一个结点都具有两个孩子（我们称它为2结点）或三个孩子（我们称它为3结点 。）

    一个2结点包含一个元素和两个孩子（或没有孩子），且与二叉排序树类似，左子树包含的元素小于该元素，右子树包含的元素大于该元素。不过，与二叉排序树不同的是，这个2结点要么没有孩子，要有就有两个，不能只有一个孩子。

    一个3结点包含一小一大两个元素和三个孩子（或没有孩子），一个3结点要么没有孩子，要么具有3个孩子。如果某个3结点有孩子的话，左子树包含小于较小元素的元素，右子树包含大于较大元素的元素，中间子树包含介于两元素之间的元素。

    并且2-3树中所有的叶子都在同一层次上。如图8-8-2所示，就是一棵有效的2-3树。

    事实上，2-3树复杂的地方就在于新结点的插入和已有结点的删除。毕竟，每个结点可能是2结点也可能是3结点，要保证所有叶子都在同一层次，是需要进行一番复杂操作的。
    image.png

    1. 2-3树的插入实现

    对于2-3树的插入来说，与二叉排序树相同，插入操作一定是发生在叶子结点上。可与二叉排序树不同的是，2-3树插入一个元素的过程有可能会对该树的其余结构产生连锁反应。

    2-3树插入可分为三种情况。

    1. 对于空树，插入一个2结点即可，这很容易理解。
    2. 插入结点到一个2结点的叶子上。应该说，由于其本身就只有一个元素，所以只需要将其升级为3结点即可。如图8-8-3所示。我们希望从左图的2-3树中插入元素3，根据遍历可知，3比8小、比4小，于是就只能考虑插入到叶子结点1所在的位置，因此很自然的想法就是将此结点变成一个3结点，即右图这样完成插入操作。当然，要视插入的元素与当前叶子结点的元素比较大小后，决定谁在左谁在右。例如，若插入的是0，则此结点就是“0”在左“1”在右了。

    image.png

    1. 要往3结点中插入一个新元素。因为3结点本身已经是2-3树的结点最大容量（已经有两个元素），因此就需要将其拆分，且将树中两元素或插入元素的三者中选择其一向上移动一层。复杂的情况也正在于此。

    第一种情况，见图8-8-4，需要向左图中插入元素5。经过遍历可得到元素5比8小比4大，因此它应该是需要插入在拥有6、7元素的3结点位置。问题就在于，6和7结点已经是3结点，不能再加。此时发现它的双亲结点4是个2结点，因此考虑让它升级为3结点，这样它就得有三个孩子，于是就想到，将6、7结点拆分，让6与4结成3结点，将5成为它的中间孩子，将7成为它的右孩子，如图8-8-4的右图所示。
    image.png
    另一种情况，如图8-8-5所示，需要向左图中插入元素11。经过遍历可得到元素11比12、14小比9、10大，因此它应该是需要插入在拥有9、10元素的3结点位置。同样道理，9和10结点不能再增加结点。此时发现它的双亲结点12、14也是一个3结点，也不能再插入元素了。再往上看，12、14结点的双亲，结点8是个2结点。于是就想到，将9、10拆分，12、14也拆分，让根结点8升级为3结点，最终形成如图8-8-5的右图样子。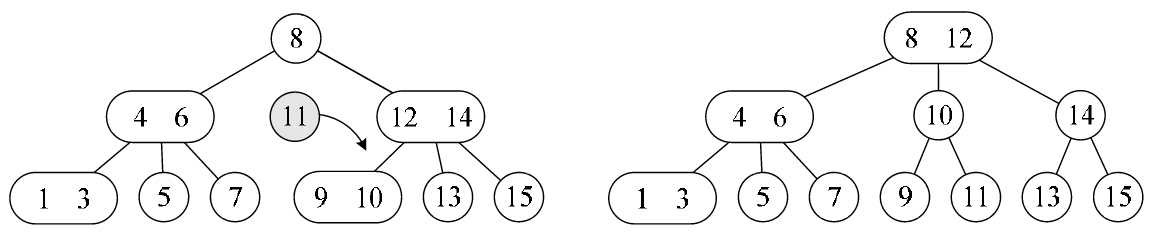
    image.png
    再来看个例子，如图8-8-6所示，需要在左图中插入元素2。经过遍历可得到元素2比4小、6比1大，因此它应该是需要插入在拥有1、3元素的3结点位置。与上例一样，你会发现，1、3结点，4、6结点都是3结点，都不能再插入元素了，再往上看，8、12结点还是一个3结点，那就意味着，当前我们的树结构是三层已经不能满足当前结点增加的需要了。于
    是将1、3拆分，4、6拆分，连根结点8、12也拆分，最终形成如图8-8-6的右图样子。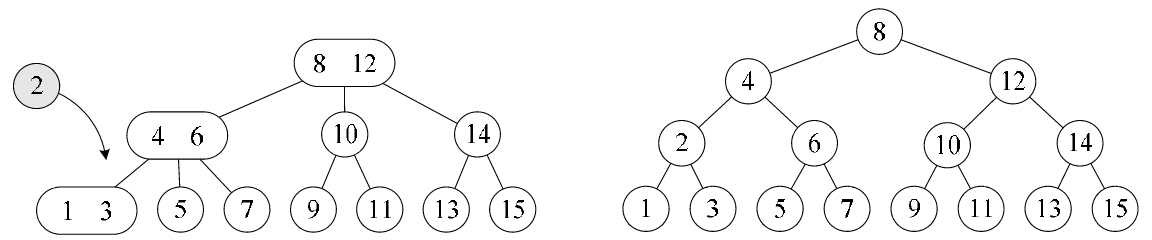
    image.png
    通过这个例子，也让我们发现，如果2-3树插入的传播效应导致了根结点的拆分，则树的高度就会增加。

    1. 2-3树的删除实现

    对于2-3树的删除来说，如果对前面插入的理解足够到位的话，应该不是难事了。2-3树的删除也分为三种情况。与插入相反，我们从3结点开始说起。

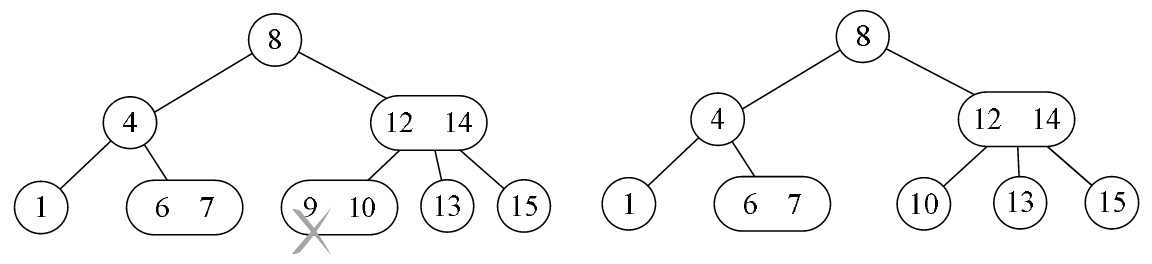
    1. 所删除元素位于一个3结点的叶子结点上， 这非常简单，只需要在该结点处删除该元素即可，不会影响到整棵树的其他结点结构。如图8-8-7所示，删除元素9，只需要将此结点改成只有元素10的2结点即可。

    image.png

    1. 所删除的元素位于一个2结点上，即要删除的是一个只有一个元素的结点。如果按照以前树的理解，删除即可，可现在的2-3树的定义告诉我们这样做是不可以的。比如图8-8-8所示，如果我们删除了结点1，那么结点4本来是一个2结点（它拥有两个孩子），此时它就不满足定义了。

    image.png 因此，对于删除叶子是2结点的情况，我们需要分四种情形来处理。

    • 情形一，此结点的双亲也是2结点，且拥有一个3结点的右孩子。如图8-8-9所示，删除结点1，那么只需要左旋，即6成为双亲，4成为6的左孩子，7是6的右孩子。

    image.png

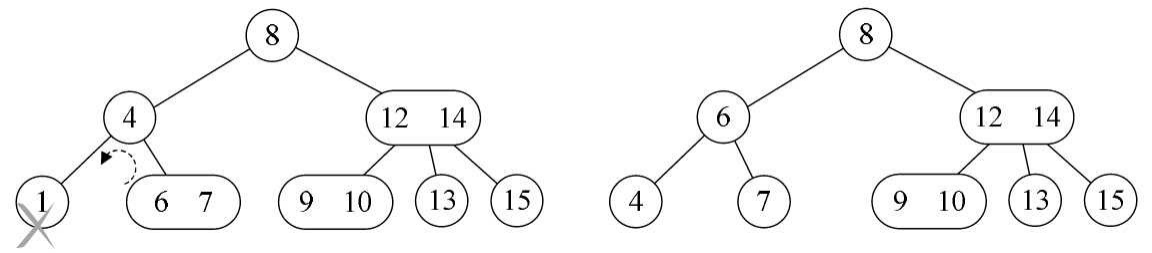
    • 情形二，此结点的双亲是2结点，它的右孩子也是2结点。如图8-8-10所示，此时删除结点4，如果直接左旋会造成没有右孩子，因此需要对整棵树变形，办法就是，我们目标是让结点7变成3结点，那就得让比7稍大的元素8下来，随即就得让比元素8稍大的元素9补充结点8的位置，于是就有了图8-8-10的中间图，于是再用左旋的方式，变成右图结果。

    image.png

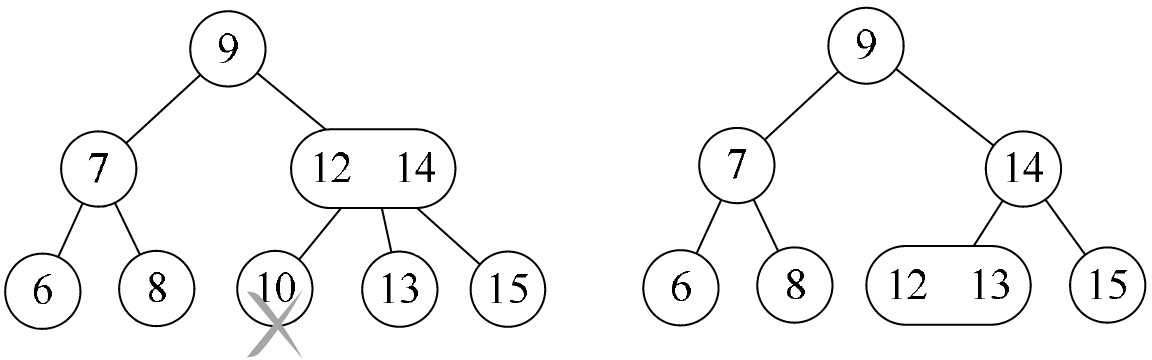
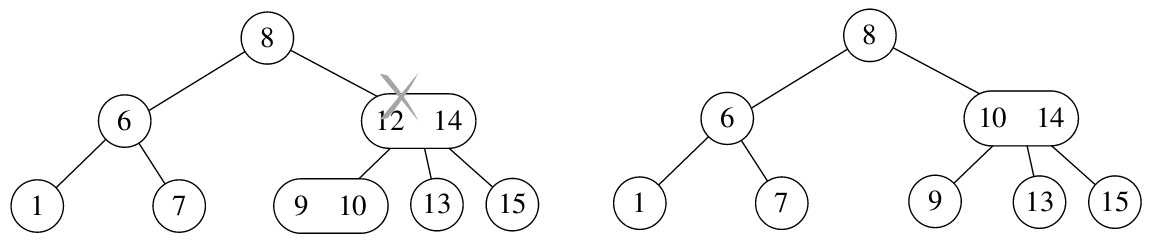
    • 情形三，此结点的双亲是一个3结点。如图8-8-11所示，此时删除结点10，意味着双亲12、14这个结点不能成为3结点了，于是将此结点拆分，并将12与13合并成为左孩子。

    image.png

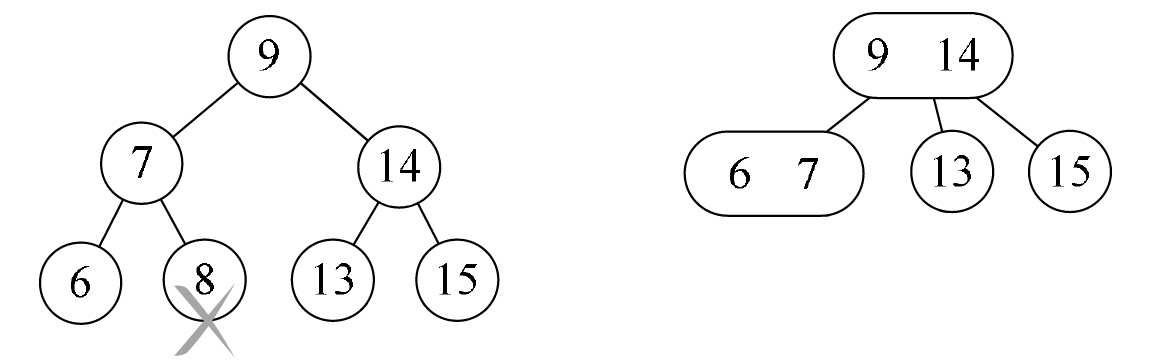
    • 情形四，如果当前树是一个满二叉树的情况，此时删除任何一个叶子都会使得整棵树不能满足2-3树的定义。如图8-8-12所示，删除叶子结点8时（其实删除任何一个结点都一样），就不得不考虑要将2-3的层数减少，办法是将8的双亲和其左子树6合并为一3个结点，再将14与9合并为3结点，最后成为右图的样子。

    image.png

    1. 所删除的元素位于非叶子的分支结点。此时我们通常是将树按中序遍历后得到此元素的前驱或后继元素，考虑让它们来补位即可。

    如果我们要删除的分支结点是2结点。如图8-8-13所示我们要删除4这个结点，分析后得到它的前驱是1后继是6，显然，由于6、7是3结点，只需要用6来补位即可，如图8-8-13右图所示。 image.png 如果我们要删除的分支结点是3结点的某一元素，如图8-8-14所示我们要删除12、14结点的12，此时，经过分析，显然应该是将是3结点的左孩子的10上升到删除位置合适。 image.png

    当然，如果对2-3树的插入和删除等所有的情况进行讲解，既占篇幅，又没必要，总的来说它是有规律的，需要你们在上面的这些例子中多去会后掌握。