有了二叉排序树的查找函数，那么所谓的二叉排序树的插入，其实也就是将关键字放到树中的合适位置而已，来看代码。

    1. /*当二叉排序树T中不存在关键字等于key的数据元素时，插入key并返回TRUE，否则返回FALSE*/
    2. StatusInsertBST(BiTree*T,intkey){
    4.     BiTree p, s;
    6.     /* 查找不成功 */
    7.     if (!SearchBST(*T, key, NULL, &p)){
    9.         s = (BiTree)malloc(sizeof(BiTNode));
    10.         s->data = key;
    11.         s->lchild = s->rchild = NULL;
    13.         if (!p)
    14.             /* 插入s为新的根结点 */
    15.             *T = s;
    16.         else if (key < p->data)
    17.             /* 插入s为左孩子 */
    18.             p->lchild = s;
    19.         else
    20.             /* 插入s为右孩子 */
    21.             p->rchild = s;
    23.         return TRUE;
    24.     }
    25.     else
    26.         /* 树中已有关键字相同的结点，不再插入 */
    27.         return FALSE;
    28. }

    这段代码非常简单。如果你调用函数是“In-sertBST(&T,93);”，那么结果就是FALSE，如果是“InsertBST(&T,95);”，那么一定就是在93的结点增加一个右孩子95，并且返回True。如图8-6-7所示。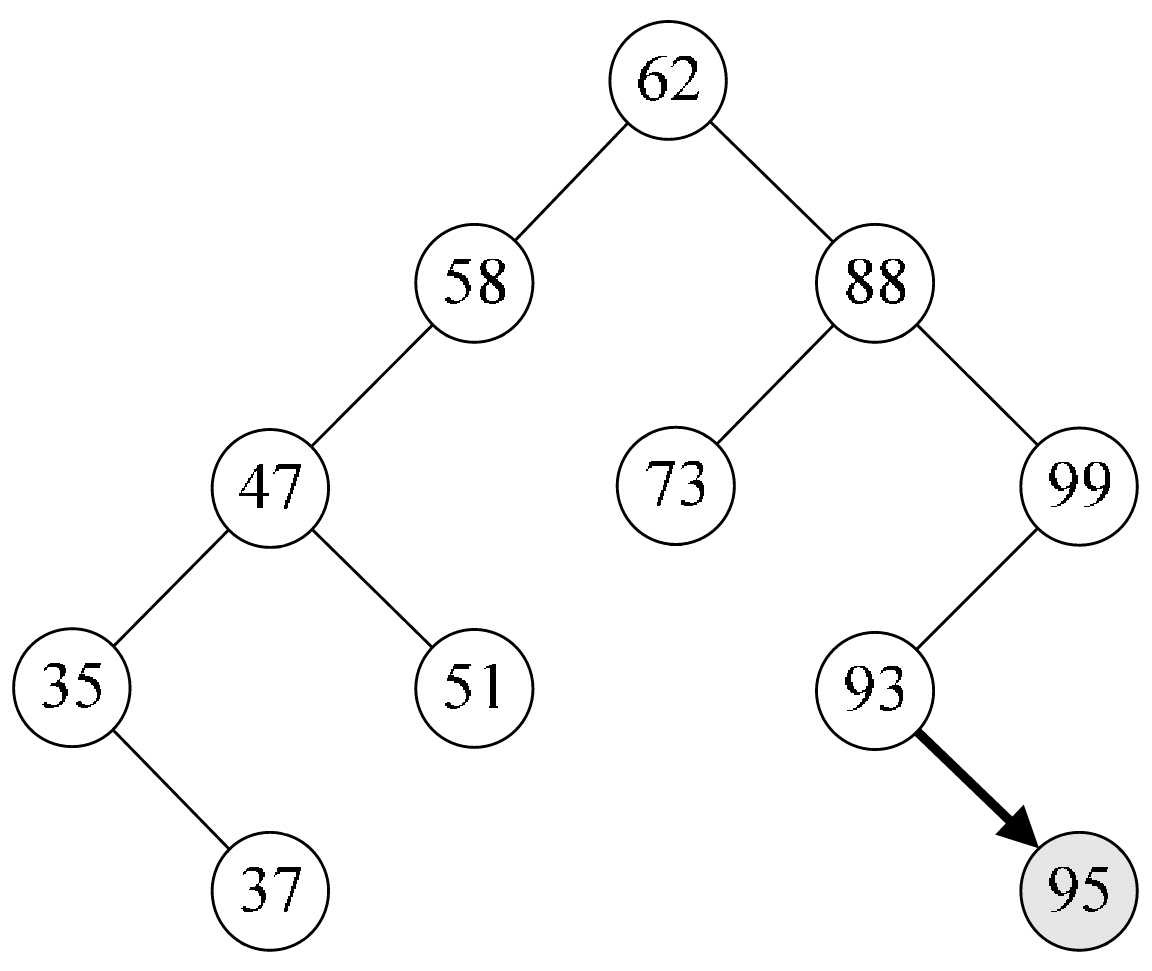
    image.png
    有了二叉排序树的插入代码，我们要实现二叉排序树的构建就非常容易了。下面的代码就可以创建一棵图8-6-3这样的树。

    1. int i;
    2. int a[10] = { 62, 88, 58, 47, 35, 73, 51,99, 37, 93 };
    3. BiTree T = NULL;
    5. for (i = 0; i < 10; i++){
    7.     InsertBST(&T, a[i]);
    8. }