这是一个按路径长度递增的次序产生最短路径的算法。它的思路大体是这样的。

    比如说要求图7-7-3中顶点v 0 到顶点v 1 的最短距离，没有比这更简单的了，答案就是1，路径就是直接v 0 连线到v 1 。

    image.png
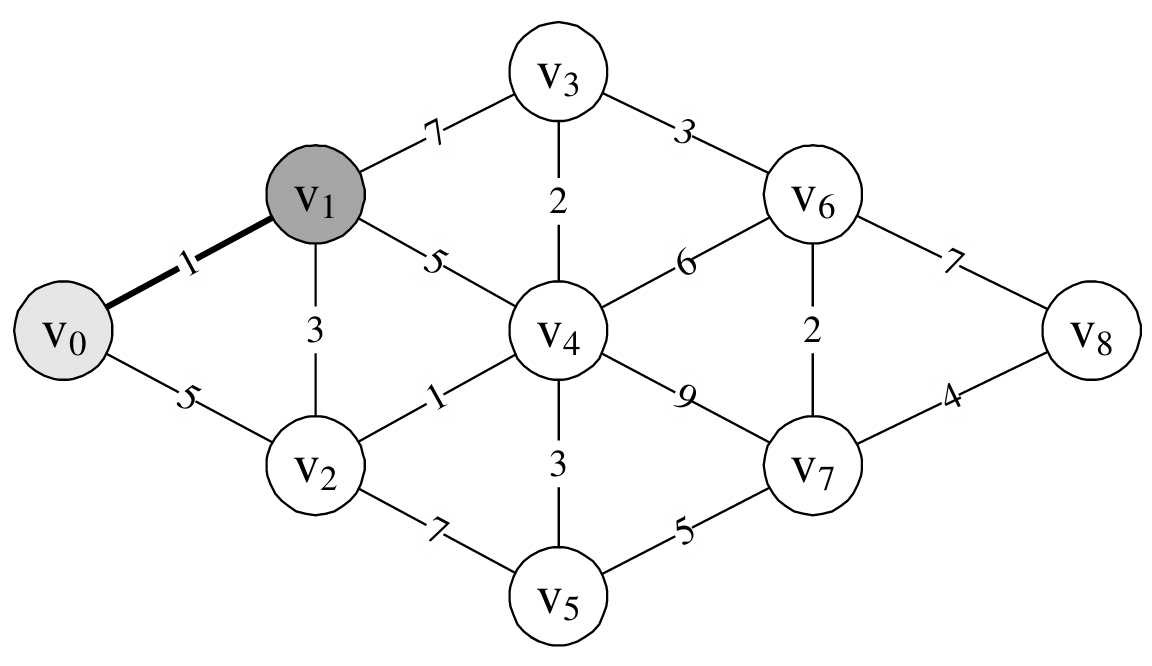
    由于顶点v 1 还与v 2 、v 3 、v 4 连线，所以此时我们同时求得了v 0 →v 1
    →v 2 =1+3=4，v 0 →v 1 → v 3 =1+7=8，v 0 →v 1 →v 4 =1+5=6。现在，
    我问v 0 到v 2 的最短距离，如果你不假思索地说是5，那就犯错了。因
    为边上都有权值，刚才已经有v 0 →v 1 →v 2 的结果是4，比5还要小1个
    单位，它才是最短距离，如图7-7-4所示。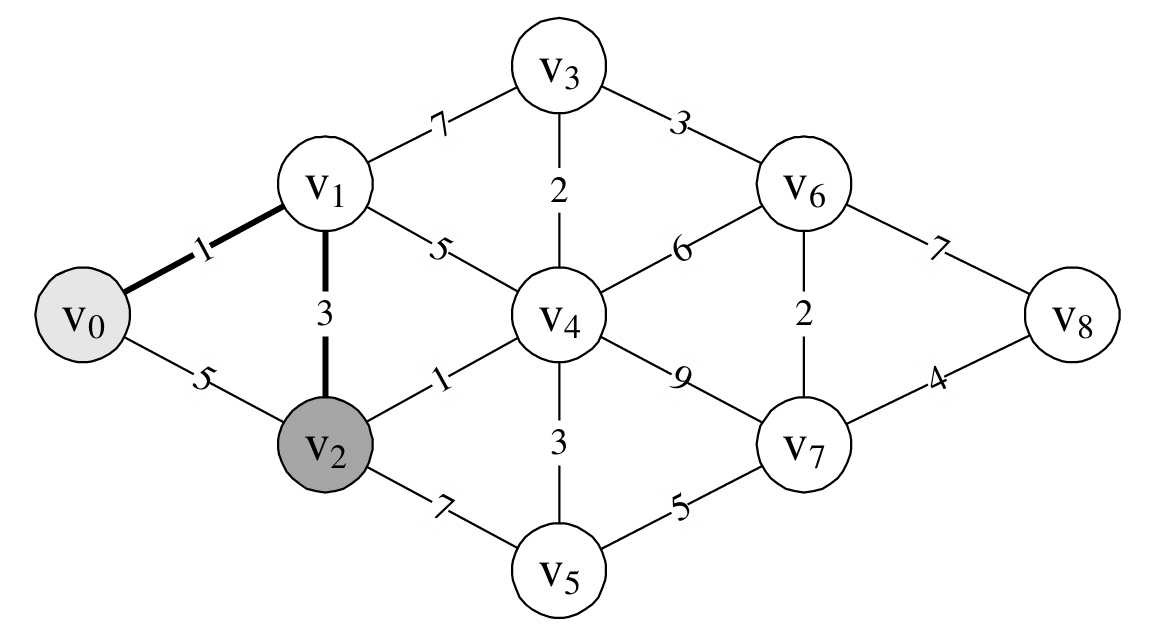
    image.png
    由于顶点v 2 还与v 4 、v 5 连线，所以此时我们同时求得了v 0 →v 2 →v 4其实就是v 0 →v 1 →v 2 →v 4 =4+1=5，v 0 →v 2 →v 5 =4+7=11。这里v 0→v 2 我们用的是刚才计算出来的较小的4。此时我们也发现v 0 →v 1 →v2 →v 4 =5要比v 0 →v 1 →v 4 =6还要小。所以v 0 到v 4 目前的最小距离是5，如图7-7-5所示。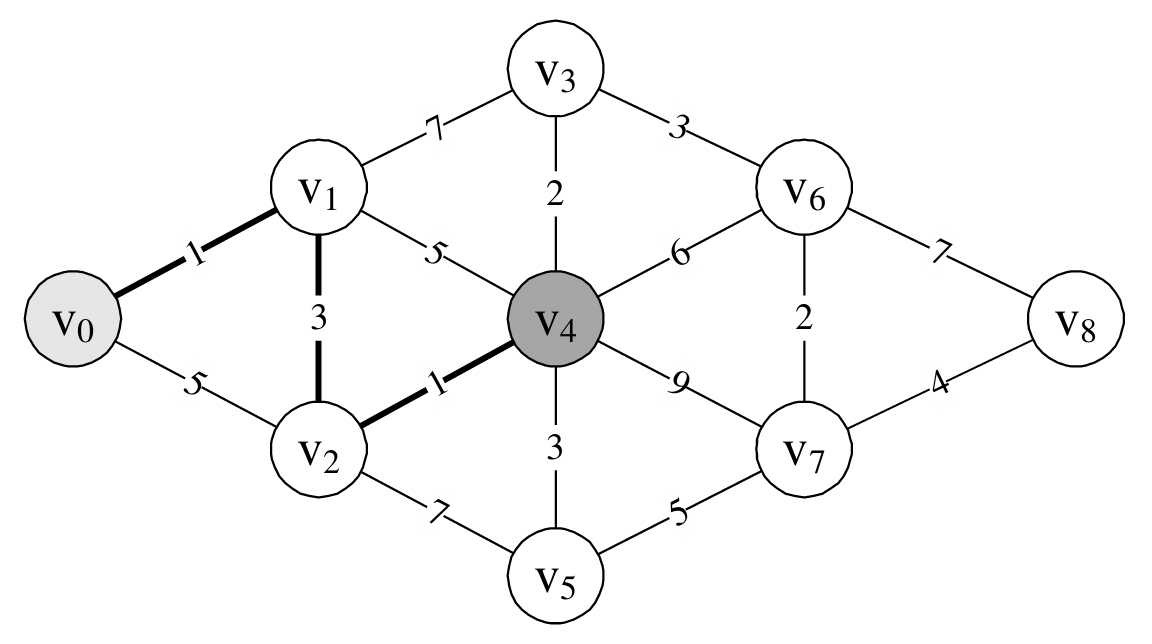
    image.png
    当我们要求v 0 到v 3 的最短距离时，通向v 3 的三条边，除了v 6 没有研究过外，v 0 →v 1 →v 3 的结果是8，而v 0 →v 4 →v 3 =5+2=7。因此，v 0 到v3 的最短距离是7，如图7-7-6所示。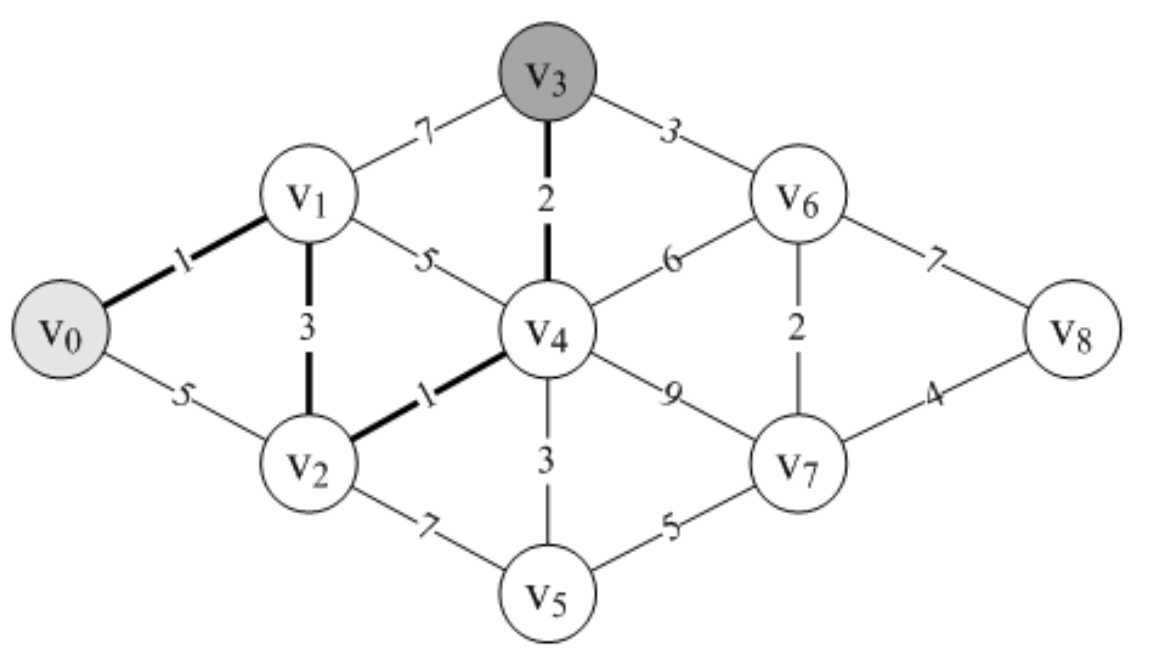
    image.png
    好了，我想你大致明白，这个迪杰斯特拉（Di-jkstra）算法是如何干活的了。它并不是一下子就求出了v 0 到v 8 的最短路径，而是一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到你要的结果。

    如果还是不太明白，不要紧，现在我们来看代码，从代码的模拟运行中，再次去理解它的思想。

    1. #define MAXVEX 9
    2. #define INFINITY 65535
    4. /* 用于存储最短路径下标的数组 */
    5. typedef int Patharc[MAXVEX];
    6. /* 用于存储到各点最短路径的权值和 */
    7. typedef int ShortPathTable[MAXVEX];
    9. /* Dijkstra算法，求有向网G的v 0 顶点到其余顶点v最短路径P[v]及带权长度D[v] */
    10. /* P[v]的值为前驱顶点下标，D[v]表示v 0 到v的最短路径长度和。 */
    11. void ShortestPath_Dijkstra(MGraph G, int v0,Patharc *P, ShortPathTable *D){
    13.     int v, w, k, min;
    14.     /* final[w]=1表示求得顶点v 0 至v w 的最短路径 */
    15.     int final[MAXVEX];
    17.     /* 初始化数据 */
    18.     for (v = 0; v < G.numVertexes; v++){
    20.     /* 全部顶点初始化为未知最短路径状态 */
    21.     final[v] = 0;
    23.     /* 将与v 0 点有连线的顶点加上权值 */
    24.     (*D)[v] = G.arc[v0][v];
    26.     /* 初始化路径数组P为-1 */
    27.     (*P)[v] = -1;
    28.     }
    30.     /* v 0 至v 0 路径为0 */
    31.     (*D)[v0] = 0;
    33.     /* v 0 至v 0 不需要求路径 */
    34.     final[v0] = 1;
    36.     /* 开始主循环，每次求得v 0 到某个v顶点的最短路径 */
    37.     for (v = 1; v < G.numVertexes; v++){
    39.         /* 当前所知离v 0 顶点的最近距离 */
    40.         min=INFINITY;
    42.         /* 寻找离v 0 最近的顶点 */
    43.         for (w = 0; w < G.numVertexes; w++){
    45.             if (!final[w] && (*D)[w] < min){
    47.             k=w;
    49.             /* w顶点离v 0 顶点更近 */
    50.             min = (*D)[w];
    51.             }
    52.         }
    54.         /* 将目前找到的最近的顶点置为1 */
    55.         final[k] = 1;
    57.         /* 修正当前最短路径及距离 */
    58.         for (w = 0; w < G.numVertexes; w++){
    60.             /* 如果经过v顶点的路径比现在这条路径的长度短的话 */
    61.             if (!final[w] && (min + G.arc[k][w] < (*D)[w])){
    63.             /* 说明找到了更短的路径，修改D[w]和P[w] */
    64.             /* 修改当前路径长度 */
    65.             (*D)[w] = min + G.arc[k][w];
    67.             (*P)[w]=k;
    68.             }
    69.         } 
    70.     } 
    71. }

    调用此函数前，其实我们需要为图7-7-7的左图准备邻接矩阵MGraph的G，如图
    7-7-7的右图，并且定义参数v 0 为0。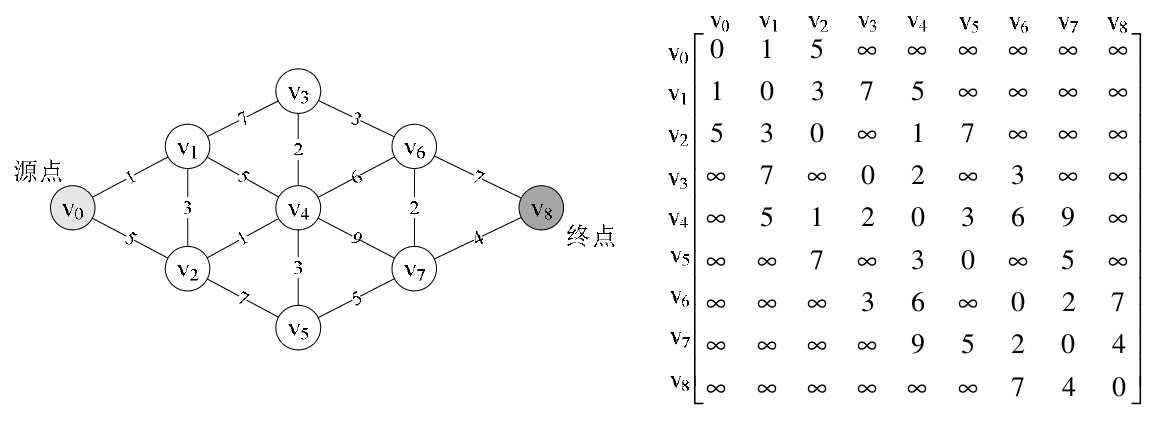
    image.png

    1. 程序开始运行，第4行final数组是为了v 0 到某顶点是否已经求得最短路径的标记，如果v 0 到v w 已经有结果，则final[w]=1。
    2. 第5～10行，是在对数据进行初始化的工作。此时final数组值均为0，表示所有的点都未求得最短路径。D数组为{65535,1,5,65535,65535,65535,65535,65535,65535}。因为v 0 与v 1 和v 2的边权值为1和5。P数组全为-1，表示目前没有路径。
    3. 第11行，表示v 0 到v 0 自身，权值和结果为0。D数组{0,1,5,65535,65535,65535,65535,65535,65535}。第12行，表示v 0 点算是已经求得最短路径，因此final[0]=1。此时final数组为{1,0,0,0,0,0,0,0,0}。此时整个初始化工作完成。
    4. 第13～33行，为主循环，每次循环求得v0 与一个顶点的最短路径。因此v从1而不是0开始。
    5. 第15～23行，先令min为65535的极大值，通过w循环，与D[w]比较找到最小值min=1，k=1。
    6. 第24行，由k=1，表示与v 0 最近的顶点是v 1 ，并且由D[1]=1，知道此时v 0 到v 1 的最短距离是1。因此将v 1 对应的final[1]设置为1。此时final数组为{1,1,0,0,0,0,0,0,0}。
    7. 第25～32行是一循环，此循环甚为关键。它的目的是在刚才已经找到v0 与v1 的最短路径的基础上，对v 1 与其他顶点的边进行计算，得到v 0 与它们的当前最短距离，如图7-7-8所示。因为min=1，所以本来D[2]=5，现在v 0 →v 1 →v 2 =D[2]=min+3=4，v 0 →v 1 →v 3 =D[3]=min+7=8，v 0 →v 1 →v 4 =D[4]=min+5=6，因此，D数组当前值为{0,1,4,8,6,65535,65535,65535,65535}。而P[2]=1，P[3]=1，P[4]=1，它表示的意思是v 0 到v 2 、v 3 、v 4 点的最短路径它们的前驱均是v 1 。此时P数组值为：{0,0,1,1,1,0,0,0,0}。

    image.png

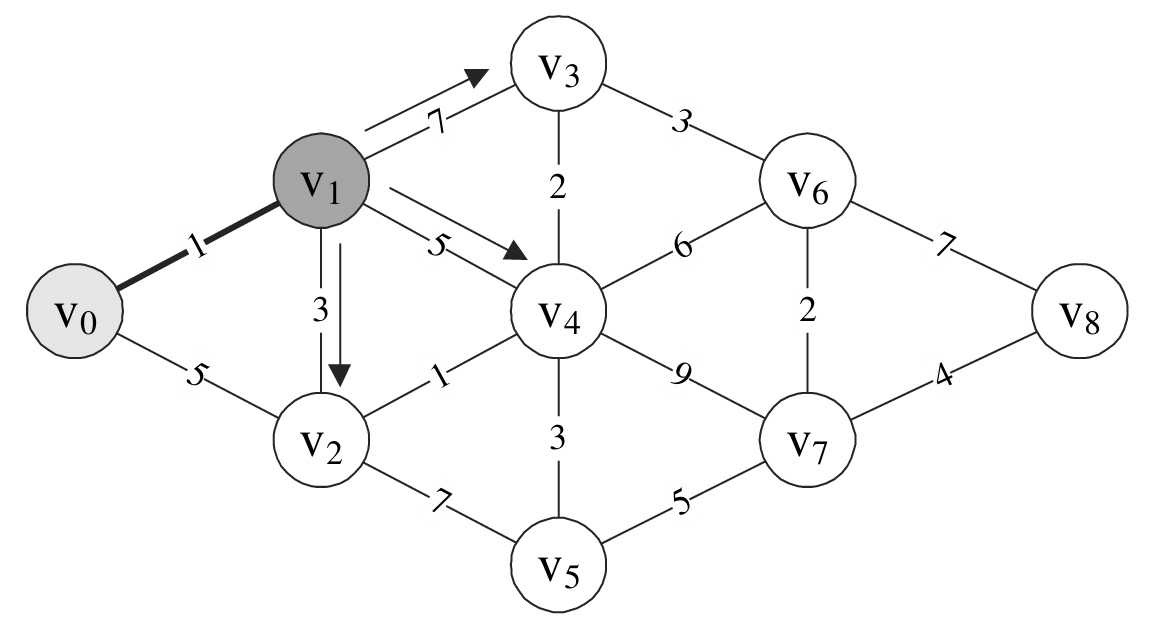
    1. 重新开始循环，此时v=2。第15～23行，对w循环，注意因为final[0]=1和final[1]=1，由第18行的!final[w]可知，v 0 与v 1 并不参与最小值的获取。通过循环比较，找到最小值min=4，k=2。
    2. 第24行，由k=2，表示已经求出v 0 到v 2 的最短路径，并且由D[2]=4，知道最短距离是4。因此将v 2 对应的final[2]设置为1，此时final数组为：{1,1,1,0,0,0,0,0,0}。10．第25～32行。在刚才已经找到v 0 与v 2的最短路径的基础上，对v 2 与其他顶点的边，进行计算，得到v 0 与它们的当前最短距离，如图7-7-9所示。因为min=4，所以本来D[4]=6，现在v 0 →v 2 →v 4 =D[4]=min+1=5，v 0 →v 2 →v 5 =D[5]=min+7=11，因此，D数组当前值为：{0,1,4,8,5,11,65535,65535,65535}。而原本P[4]=1，此时P[4]=2，P[5]=2，它表示v 0 到v 4 、v 5 点的最短路径它们的前驱均是v 2 。此时P数组值为：{0,0,1,1,2,2,0,0,0}。

    image.png

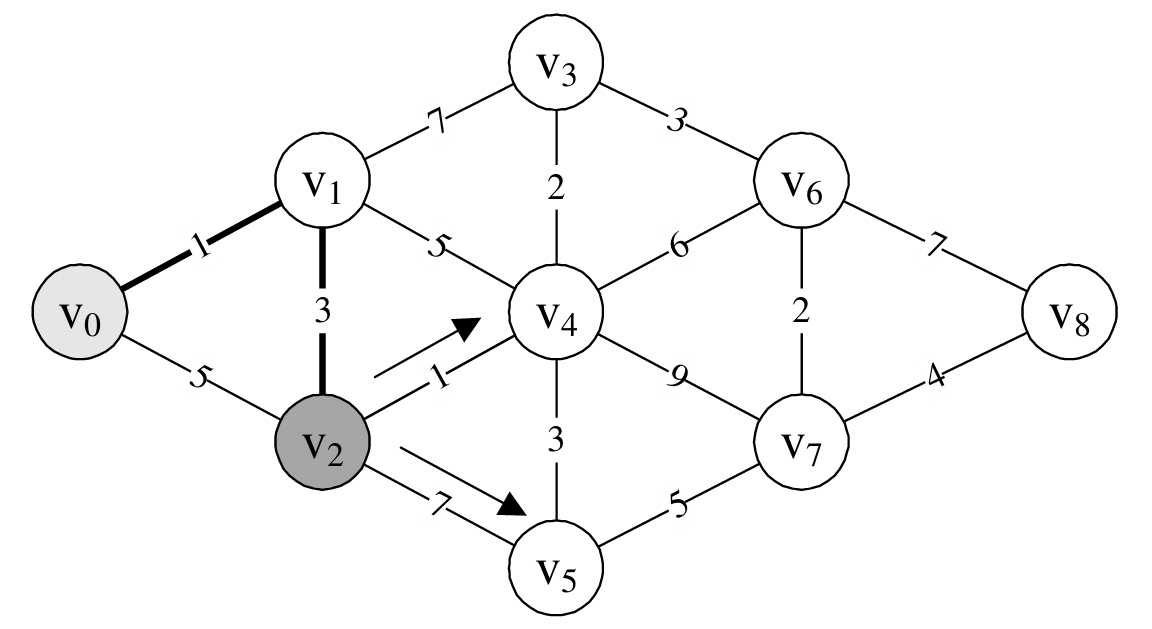
    1. 重新开始循环，此时v=3。第15～23行，通过对w循环比较找到最小值min=5，k=4。12．第24行，由k=4，表示已经求出v 0 到v 4 的最短路径，并且由D[4]=5，知道最短距离是5。因此将v 4 对应的final[4]设置为1。此时final数组为：{1,1,1,0,1,0,0,0,0}。13．第25～32行。对v 4 与其他顶点的边进行计算，得到v 0 与它们的当前最短距离，如图7-7-10所示。因为min=5，所以本来D[3]=8，现在v 0 →v 4 →v 3 =D[3]=min+2=7，本来D[5]=11，现在v 0 →v 4 →v 5 =D[5]=min+3=8，另外v 0 →v 4 →v 6 =D[6]=min+6=11，v 0 →v 4 →v 7 =D[7]=min+9=14，因此，D数组当前值为：{0,1,4,7,5,8,11,14,65535}。而原本P[3]=1，此时P[3]=4，原本P[5]=2，此时P[5]=4，另外P[6]=4，P[7]=4，它表示v 0 到v 3 、v 5 、v 6 、v 7 点的最短路径它们的前驱均是v 4 。此时P数组值为：{0,0,1,4,2,4,4,4,0}。

    image.png

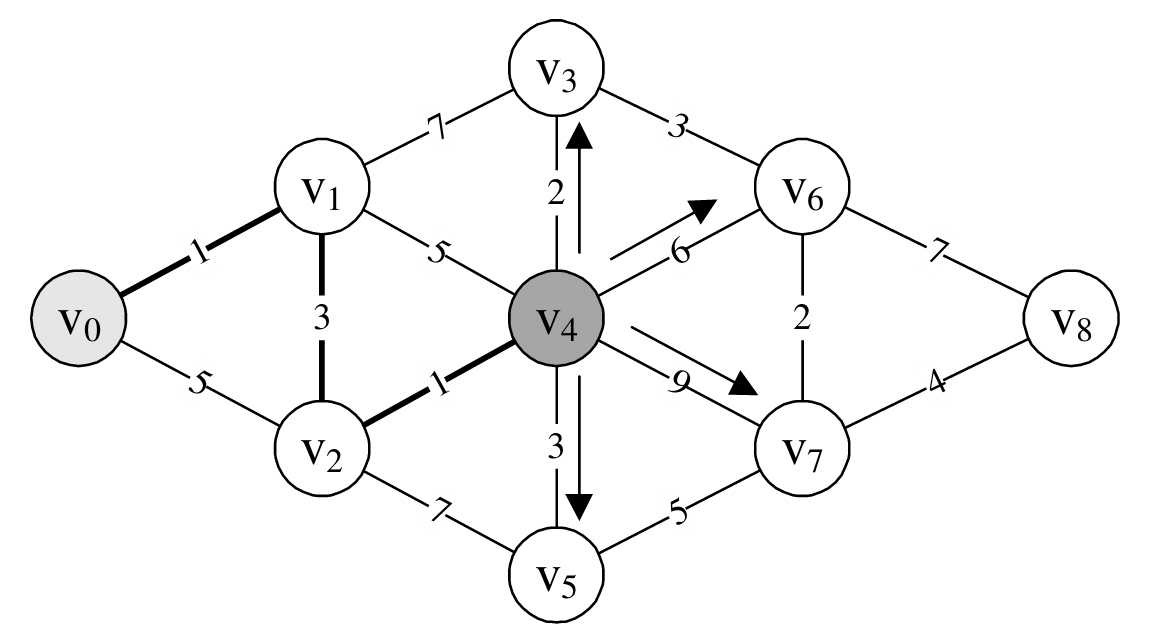
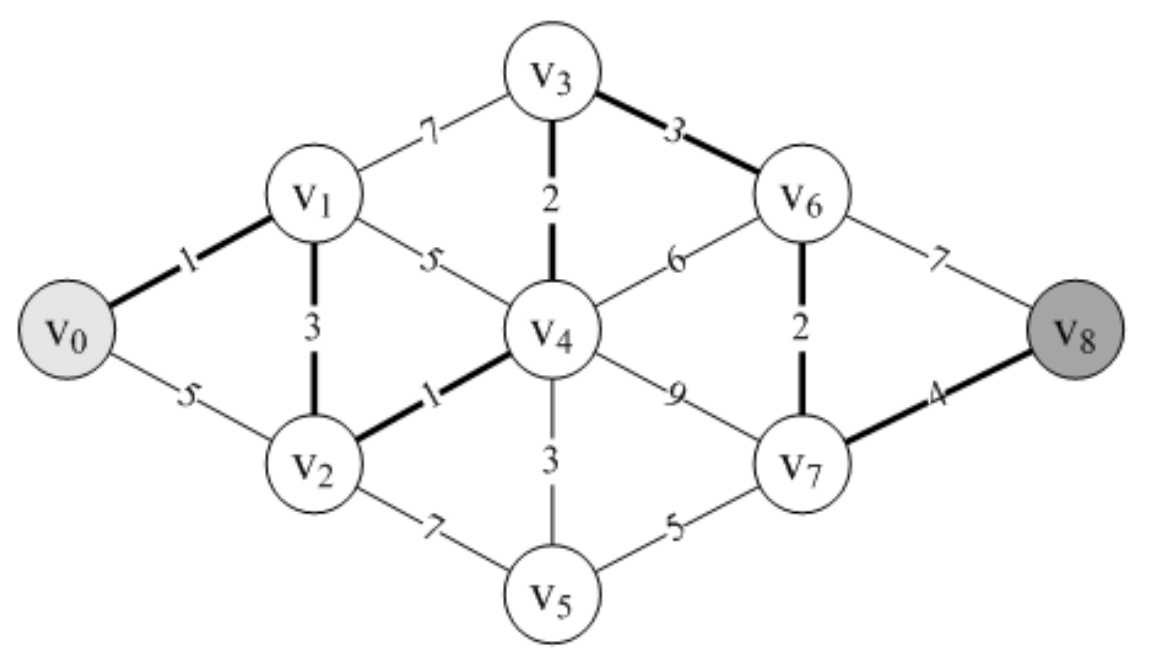
    1. 之后的循环就完全类似了。得到最终的结果，如图7-7-11所示。此时final数组为：{1,1,1,1,1,1,1,1,1}，它表示所有的顶点均完成了最短路径的查找工作。此时D数组为：{0,1,4,7,5,8,10,12,16}，它表示v 0 到各个顶点的最短路径数，比如D[8]=1+3+1+2+3+2+4=16。此时的P数组为：{0,0,1,4,2,4,3,6,7}，这串数字可能略为难理解一些。比如P[8]=7，它的意思是v 0 到v 8 的最短路径，顶点v 8 的前驱顶点是v 7 ，再由P[7]=6表示v 7 的前驱是v 6 ，P[6]=3，表示v 6 的前驱是v 3 。这样就可以得到，v 0 到v 8 的最短路径为v 8 ←v 7 ←v6 ←v 3 ←v 4 ←v 2 ←v 1 ←v 0 ，即v 0 →v 1→v 2 →v 4 →v 3 →v 6 →v 7 →v 8 。

    image.png
    其实最终返回的数组D和数组P，是可以得到v 0 到任意一个顶点的最短路径和路径长度的。例如v 0 到v 8 的最短路径并没有经过v 5 ，但我们已经知道v 0 到v 5 的最短路径了。由D[5]=8可知它的路径长度为8，由P[5]=4可知v 5 的前驱顶点是v 4 ，所以v 0 到v 5 的最短路径是v 0 →v 1 →v2→v 4 →v 5 。

    也就是说，我们通过迪杰斯特拉（Dijkstra）算法解决了从某个源点到其余各顶点的最短路径问题。从循环嵌套可以很容易得到此算法的时间复杂度为O(n 2 )，尽管有同学觉得，可不可以只找到从源点到某一个特定终点的最短路径，其实这个问题和求源点到其他所有顶点的最短路径一样复杂，时间复杂度依然是O(n 2 )。

    这就好比，你吃了七个包子终于算是吃饱了，就感觉很不划算，前六个包子白吃了，应该直接吃第七个包子，于是你就去寻找可以吃一个就能饱肚子的包子，能够满足你的要求最终结果只能有一个，那就是用七个包子的面粉和馅做的一个大包子。这种只关注结果而忽略过程的思想是非常不可取的。

    可如果我们还需要知道如v 3 到v 5 、v 1 到v 7 这样的任一顶点到其余所有顶点的最短路径怎么办呢？此时简单的办法就是对每个顶点当作源点运行一次迪杰斯特拉（Dijkstra）算法，等于在原有算法的基础上，再来一次循环，此时整个算法的时间复杂度就成了O(n 3 )。

    对此，我们现在再来介绍另一个求最短路径的算法——弗洛伊德（Floyd），它求所有顶点到所有顶点的时间复杂度也是O(n3 )，

    但其算法非常简洁优雅，能让人感觉到智慧的无限魅力。好了，让我们就一同来欣赏和学习它吧。