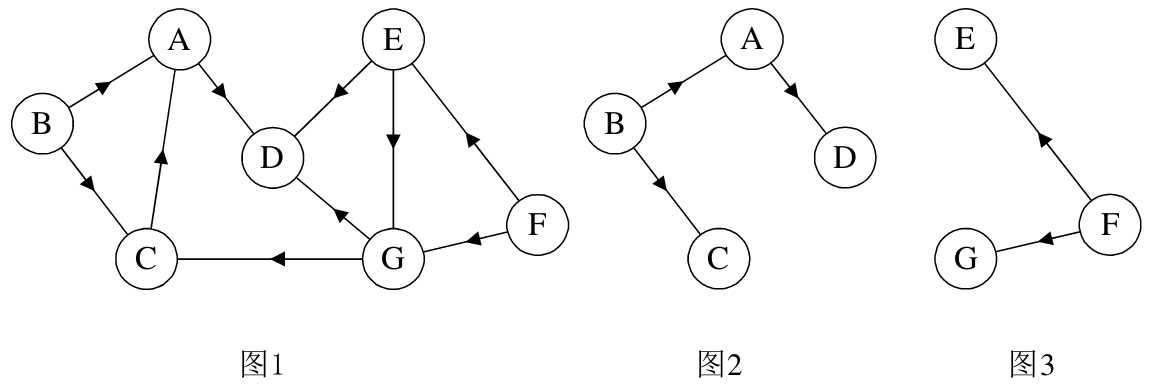
在无向图G中,如果从顶点v到顶点v’有路径,则称v和v’是连通的。如果对于图中任意两个顶点v i 、v j ∈V,v i 和v j 都是连通的,则称G是连通图(Connected Graph)。图7-2-12的图1,它的顶点A到顶点B、C、D都是连通的,但显然顶点A与顶点E或F就无路径,因此不能算是连通图。而图7-2-12的图2,顶点A、B、C、D相互都是连通的,所以它本身是连通图。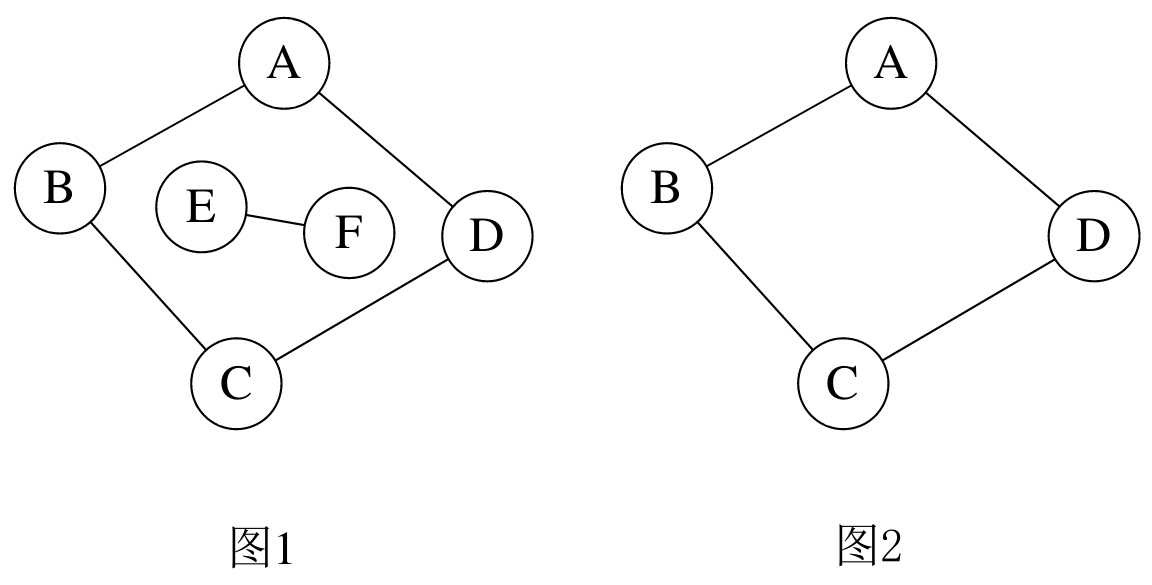
无向图中的极大连通子图称为连通分量。注意连通分量的概念,它强调:
- 要是子图;
- 子图要是连通的;
- 连通子图含有极大顶点数;
- 具有极大顶点数的连通子图包含依附于这些顶点的所有边。
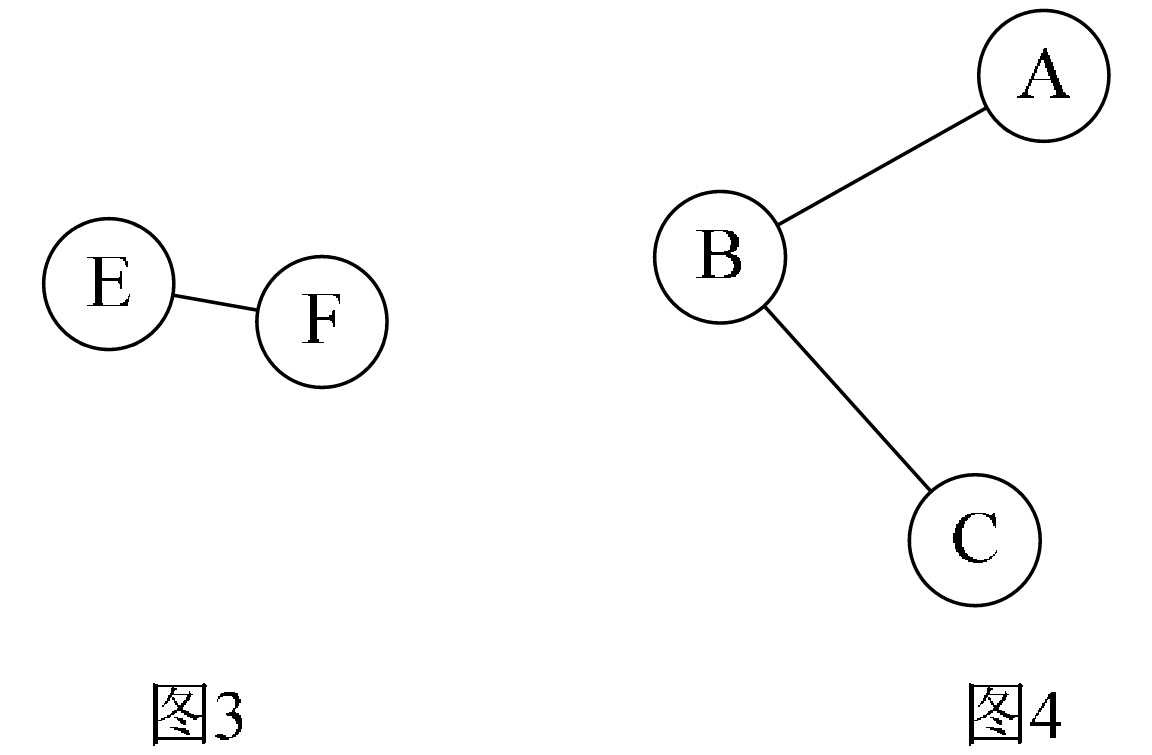
图7-2-12的图1是一个无向非连通图。但是它有两个连通分量,即图2和图3。而图4,尽管是图1的子图,但是它却不满足连通子图的极大顶点数(图2满足)。因此它不是图1的无向图的连通分量。
在有向图G中,如果对于每一对v i 、v j ∈V、v i ≠v j ,从v i 到v j 和从v j到v i 都存在路径,则称G是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。例如图7-2-13,图1并不是强连通图,因为顶点A到顶点D存在路径,而D到A就不存在。图2就是强连通图,而且显然图2是图1的极大强连通子图,即是它的强连通分量。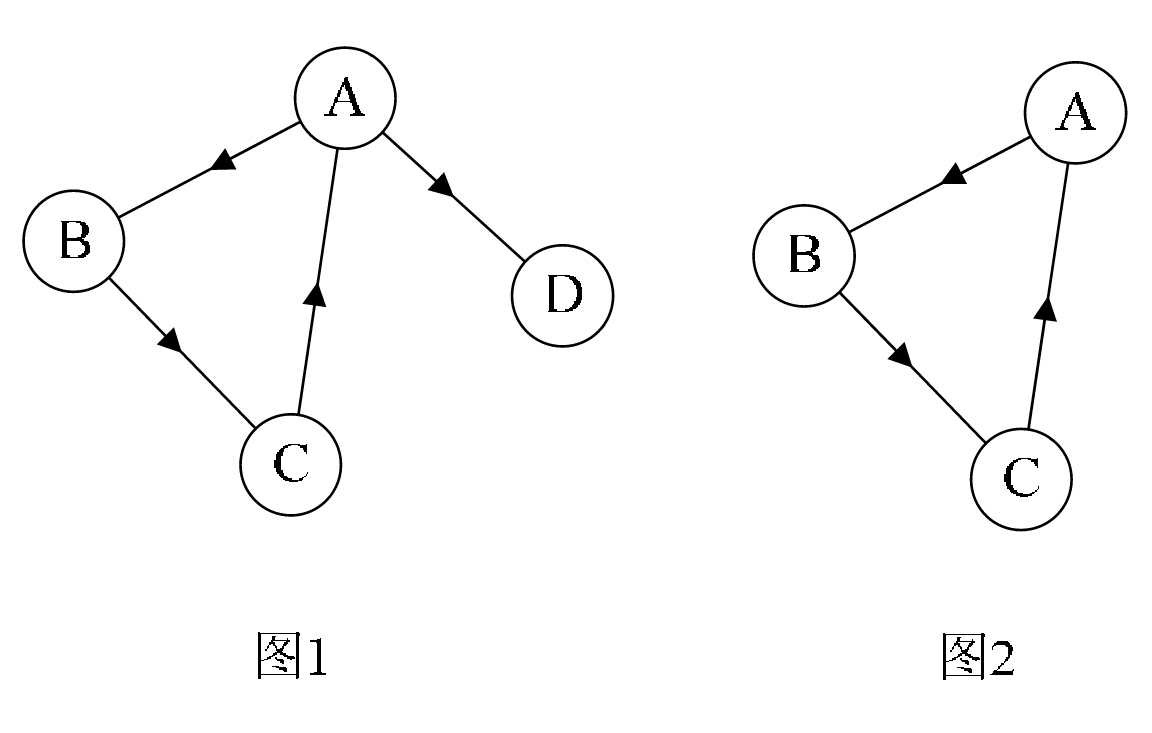
现在我们再来看连通图的生成树定义。
所谓的一个连通图的生成树是一个极小的连通子图,它含有图中全部的n个顶点,但只有足以构成一棵树的n-1条边。比如图7-2-14的图1是一普通图,但显然它不是生成树,当去掉两条构成环的边后,比如图2或图3,就满足n个顶点n-1条边且连通的定义了。它们都是一棵生成树。从这里也可知道,如果一个图有n个顶点和小于n-1条边,则是非连通图,如果它多于n-1条边,必定构成一个环,因为这条边使得它依附的那两个顶点之间有了第二条路径。比如图2和图3,随便加哪两顶点的边都将构成环。不过有n-1条边并不一定是生成树,比如图4。 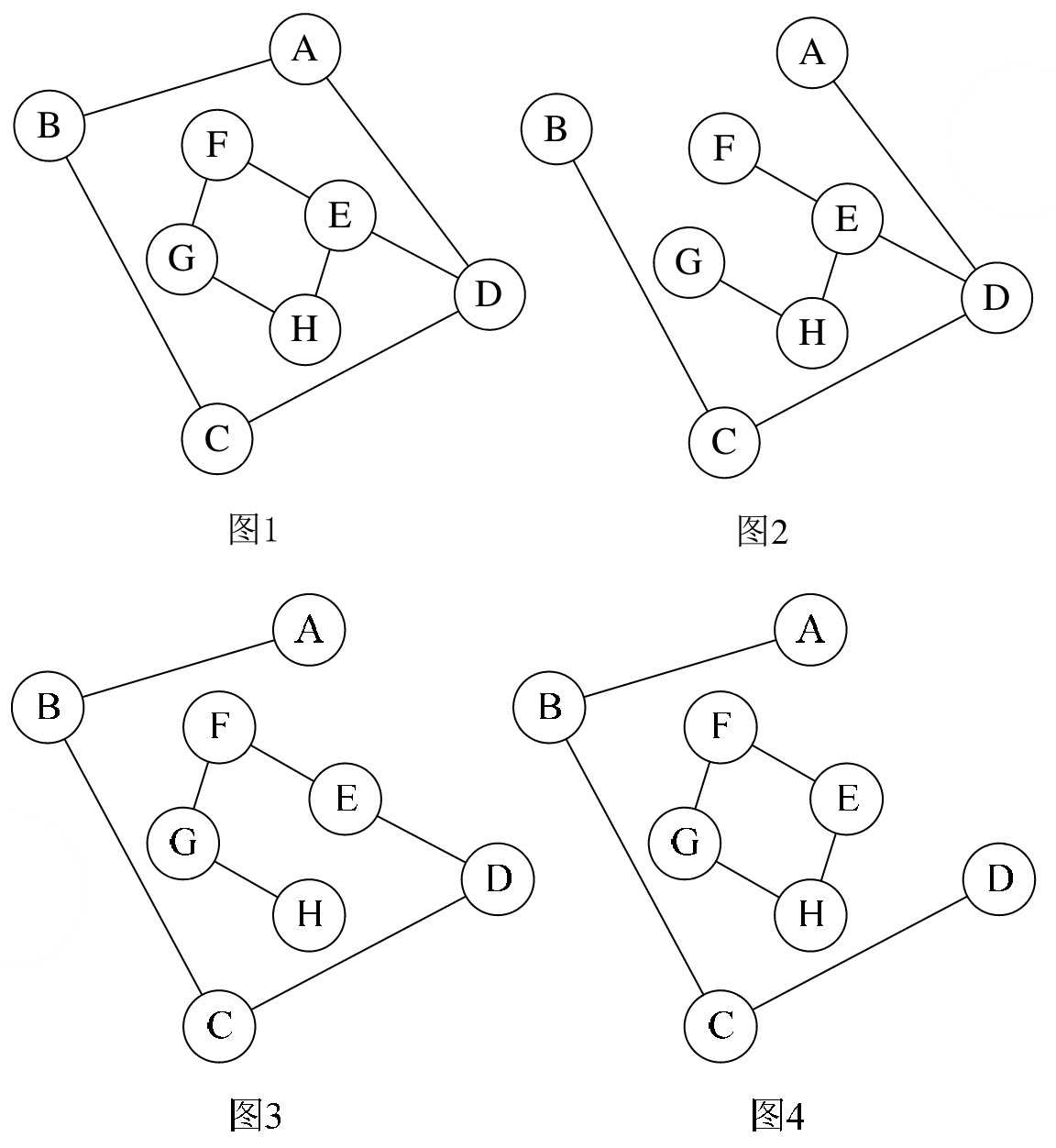
如果一个有向图恰有一个顶点的入度为0,其余顶点的入度均为1,则是一个有向树。对有向树的理解比较容易,所谓入度为0其实就相当于树中的根结点,其余顶点入度为1就是说树的非根结点的双亲只有一个。一个有向图的生成森林由若干棵有向树组成,含有图中全部顶点,但只有足以构成若干棵不相交的有向树的弧。如图7-2-15的图1是一棵有向图。去掉一些弧后,它可以分解为两棵有向树,如图2和图3,这两棵就是图1有向图的生成森林。