俗话说“请神容易送神难”，我们已经介绍了二叉排序树的查找与插入算法，但是对于二叉排序树的删除，就不是那么容易，我们不能因为删除了结点，而让这棵树变得不满足二叉排序树的特性，所以删除需要考虑多种情况。

    如果需要查找并删除如37、51、73、93这些在二叉排序树中是叶子的结点，那是很容易的，毕竟删除它们对整棵树来说，其他结点的结构并未受到影响，如图8-6-8所示。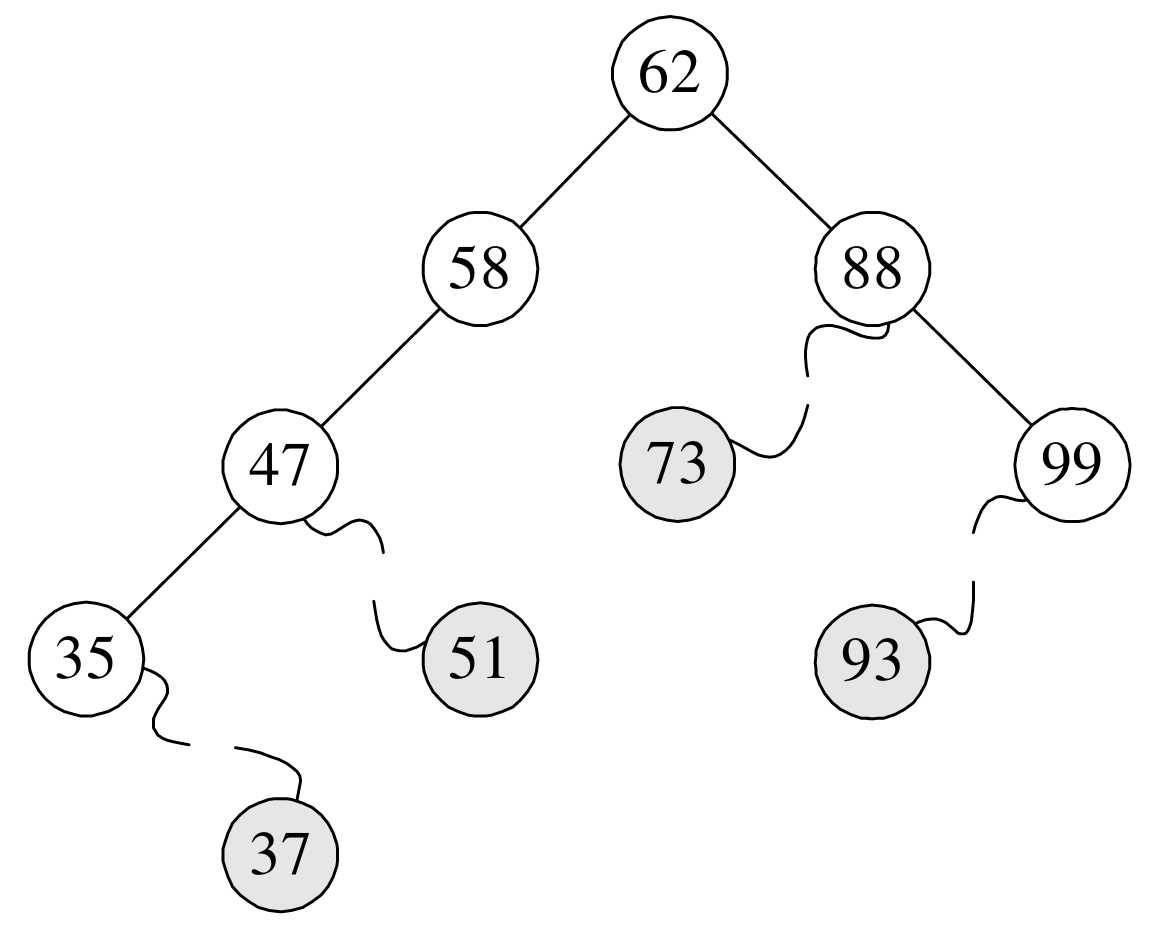
    image.png
    对于要删除的结点只有左子树或只有右子树的情况，相对也比较好解决。那就是结点删除后，将它的左子树或右子树整个移动到删除结点的位置即可，可以理解为独子继承父业。比如图8-6-9，就是先删除35和99结点，再删除58结点的变化图，最终，整个结构还是一个二叉排序树。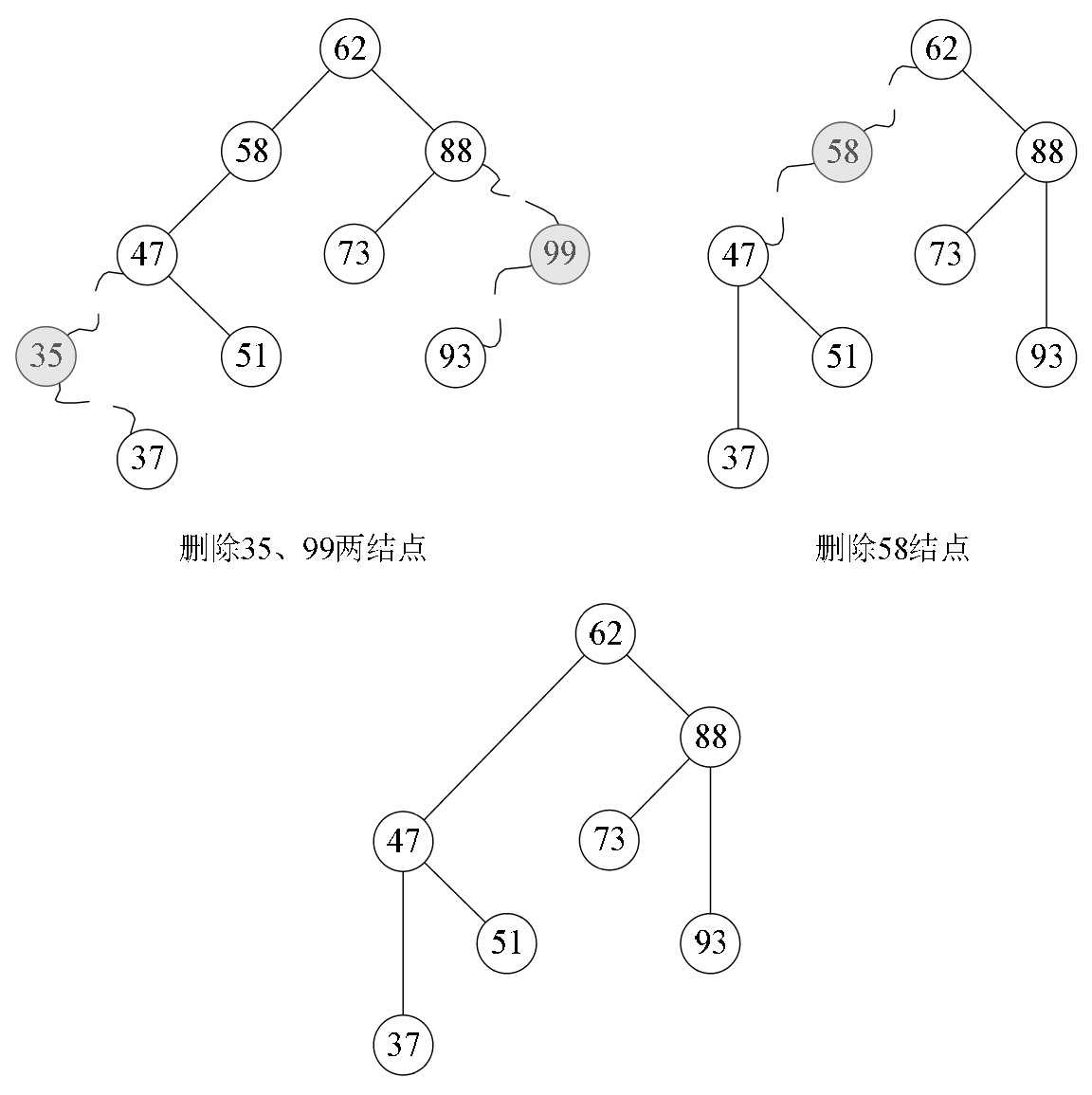
    image.png
    但是对于要删除的结点既有左子树又有右子树的情况怎么办呢？比如图8-6-10中的47结点若要删除了，它的两儿子以及子孙们怎么办呢？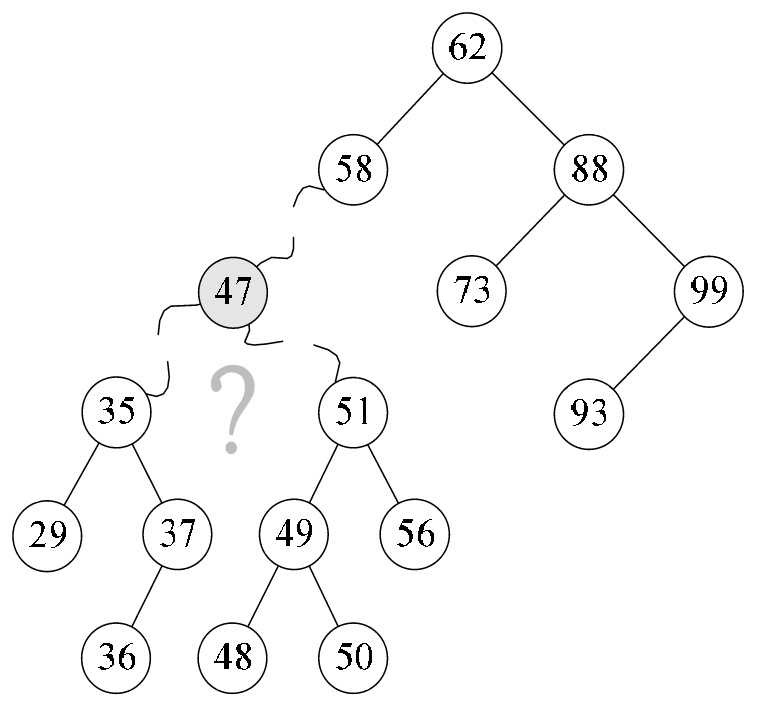
    image.png
    起初的想法，我们当47结点只有一个左子树，那么做法和一个左子树的操作一样，让35及它之下的结点成为58的左子树，然后再对47的右子树所有结点进行插入操作，如图8-6-11所示。这是比较简单的想法，可是47的右子树有子孙共5个结点，这么做效率不高且不说，还会导致整个二叉排序树结构发生很大的变化，有可能会增加树的高度。增加高度可不是个好事，这我们待会再说，总之这个想法不太好。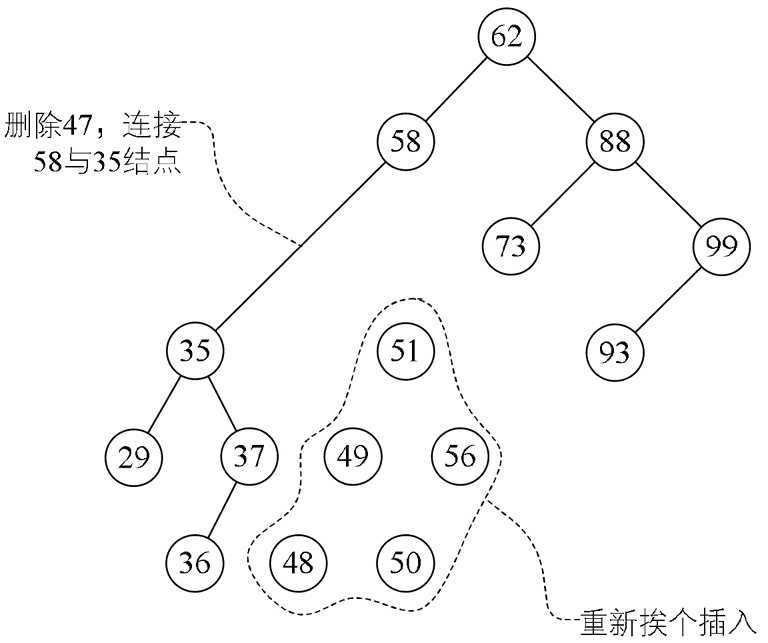
    image.png
    我们仔细观察一下，47的两个子树中能否找出一个结点可以代替47呢？果然有，37或者48都可以代替47，此时在删除47后，整个二叉排序树并没有发生什么本质的改变。

    为什么是37和48？对的，它们正好是二叉排序树中比它小或比它大的最接近47的两个数。也就是说，如果我们对这棵二叉排序树进行中序遍历，得到的序列{29,35,36,37,47,48,49,50,51,56,58,62,73,88,93,99}，它们正好是47的前驱和后继。

    因此，比较好的办法就是，找到需要删除的结点p的直接前驱（或直接后继）s，用s来替换结点p，然后再删除此结点s，如图8-6-12所示。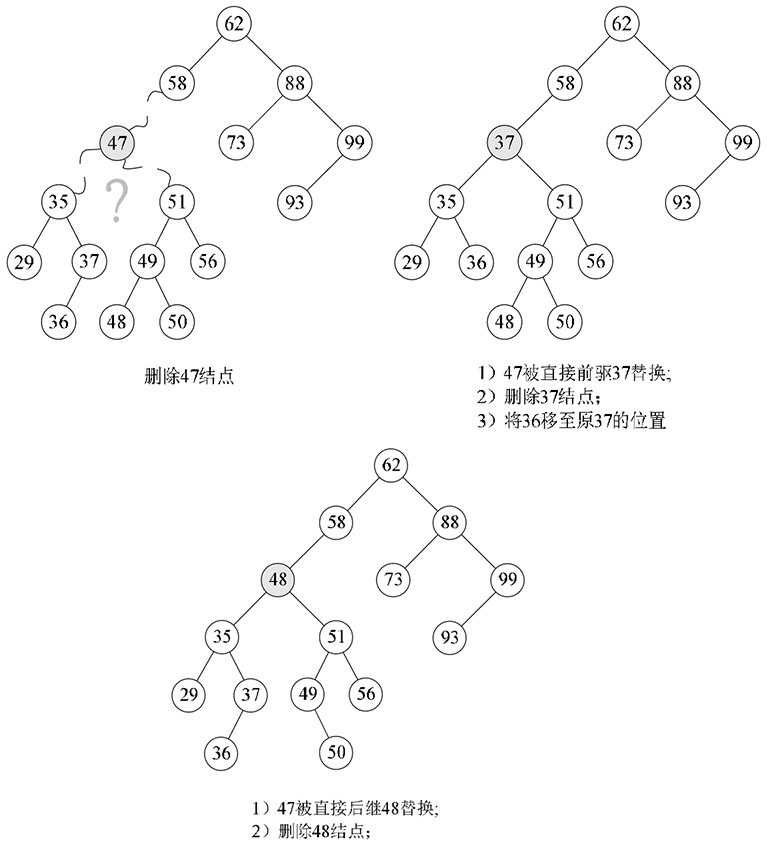
    image.png
    根据我们对删除结点三种情况的分析：

    • 叶子结点；
    • 仅有左或右子树的结点；
    • 左右子树都有的结点


    我们来看代码，下面这个算法是递归方式对二叉排序树T查找key，查找到时删除。 

    1. /* 若二叉排序树T中存在关键字等于key的数据元素 时，则删除该数据元素结点, */ 
    2. /* 并返回TRUE；否则返回FALSE */ 
    3. Status DeleteBST(BiTree *T, int key) { 
    5.     /* 不存在关键字等于key的数据元素 */ 
    6.     if (!*T) 
    7.         return FALSE; 
    8.     else {
    10.         /* 找到关键字等于key的数据元素 */ 
    11.         if (key == (*T)->data) 
    12.             return Delete(T); 
    13.         else if (key < (*T)->data) 
    14.             return DeleteBST(&(*T)->lchild, key); 
    15.         else
    16.             return DeleteBST(&(*T)->rchild, key);
    17.     } 
    18. }

    这段代码和前面的二叉排序树查找几乎完全相同，唯一的区别就在于第8行，此时执行的是Delete方法，对当前结点进行删除操作。我们来看Delete的代码。

    1. /* 从二叉排序树中删除结点p，并重接它的左或右子树。 */ 
    2. Status Delete(BiTree *p) { 
    4.     BiTree q, s; 
    5.     /* 右子树空则只需重接它的左子树 */ 
    6.     if ((*p)->rchild == NULL) {
    8.         q = *p;
    9.         *p = (*p)->lchild;
    10.         free(q);
    11.     }
    12.     /* 只需重接它的右子树 */ 
    13.     else if ((*p)->lchild == NULL) {
    15.         q = *p;
    16.         *p = (*p)->rchild;
    17.         free(q);
    18.     }
    19.     /* 左右子树均不空 */
    20.     else {
    21.         q = *p;
    22.         s = (*p)->lchild;
    23.         /* 转左，然后向右到尽头(找待删结点的前驱) */
    24.         while (s->rchild) {
    26.             q = s;
    27.             s = s->rchild;
    28.         }
    30.         /* s指向被删结点的直接前驱 */
    31.         (*p)->data = s->data;
    33.         if (q != *p)
    34.             /* 重接q的右子树 */
    35.             q->rchild = s->lchild;
    36.         else
    37.             /* 重接q的左子树 */ 
    38.             q->lchild = s->lchild;
    40.         free(s);
    41.     }
    42.     return TRUE; 
    43. }
    1. 程序开始执行，代码第4～7行目的是为了删除没有右子树只有左子树的结点。此时只需将此结点的左孩子替换它自己，然后释放此结点内存，就等于删除了。
    2. 代码第8～11行是同样的道理处理只有右子树没有左子树的结点删除问题。
    3. 第12～25行处理复杂的左右子树均存在的问题。
    4. 第14行，将要删除的结点p赋值给临时的变量q，再将p的左孩子p->lchild赋值给临时的变量s。此时q指向47结点，s指向35结点，如图8-6-13所示。

    image.png

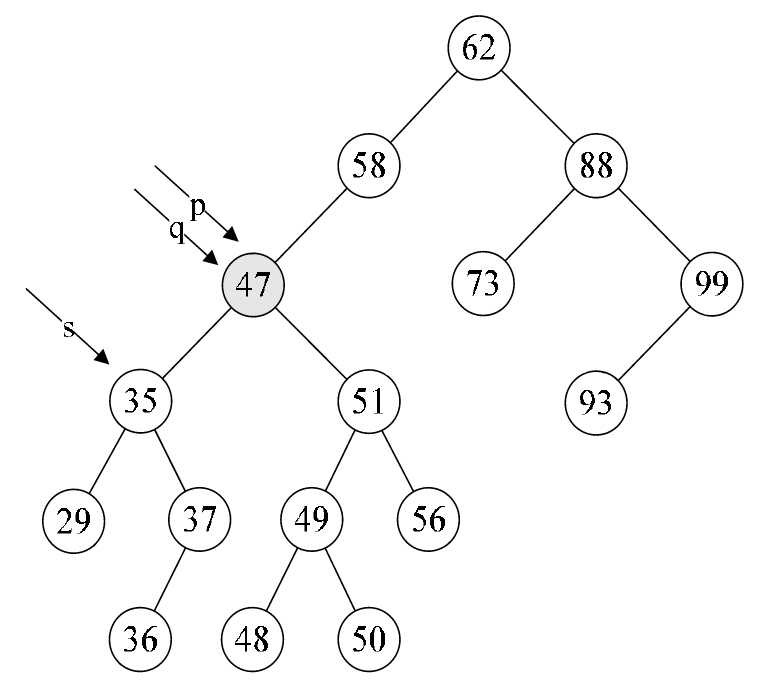
    1. 第15～18行，循环找到左子树的右结点，直到右侧尽头。就当前例子来说就是让q指向35，而s指向了37这个再没有右子树的结点，如图8-6-14所示。

    image.png

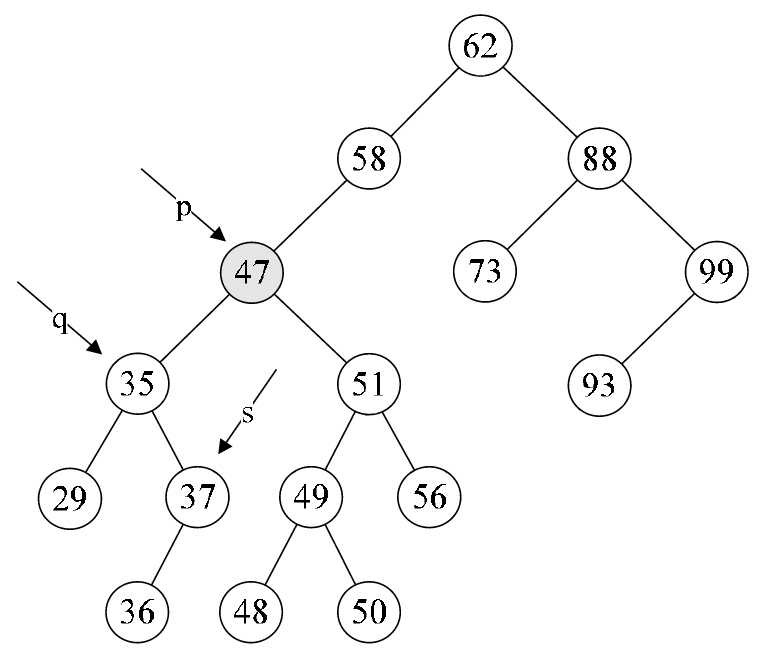
    1. 第19行，此时让要删除的结点p的位置的数据被赋值为s->data，即让p->data=37，如图8-6-15所示。

    image.png

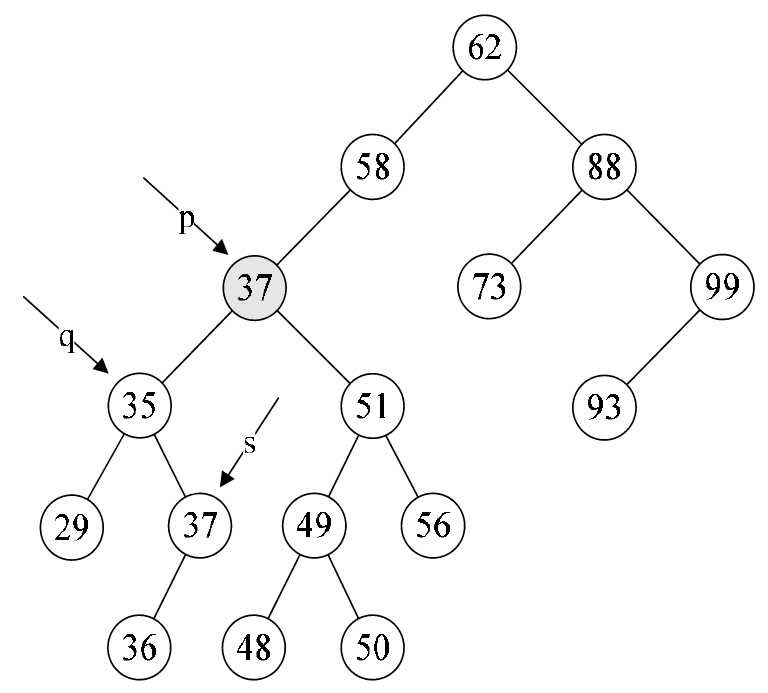
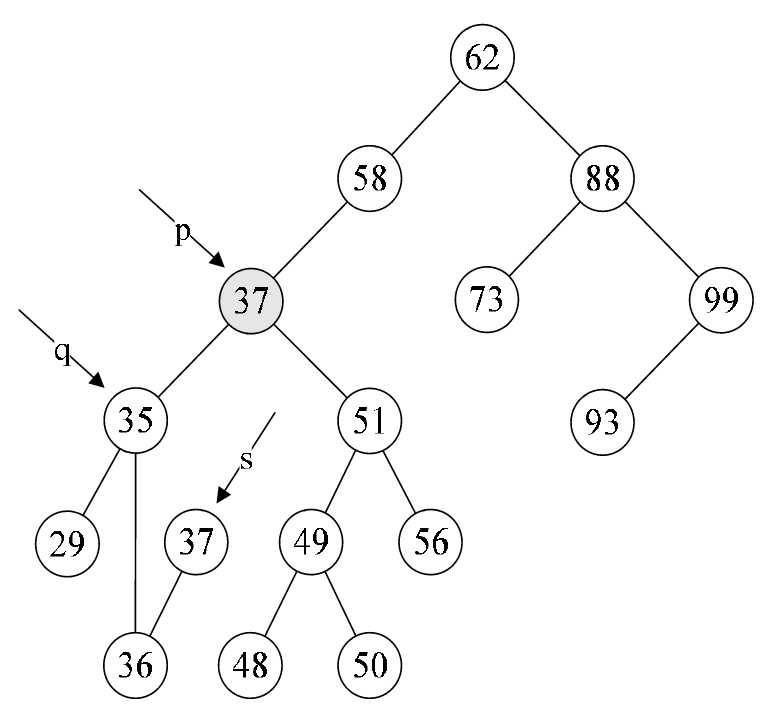
    1. 第20～23行，如果p和q指向不同，则将s->lchild赋值给q->rchild，否则就是将s->lchild赋值给q->lchild。显然这个例子p不等于q，将s->lchild指向的36赋值给q->rchild，也就是让q->rchild指向36结点，如图8-6-16所示。

    image.png

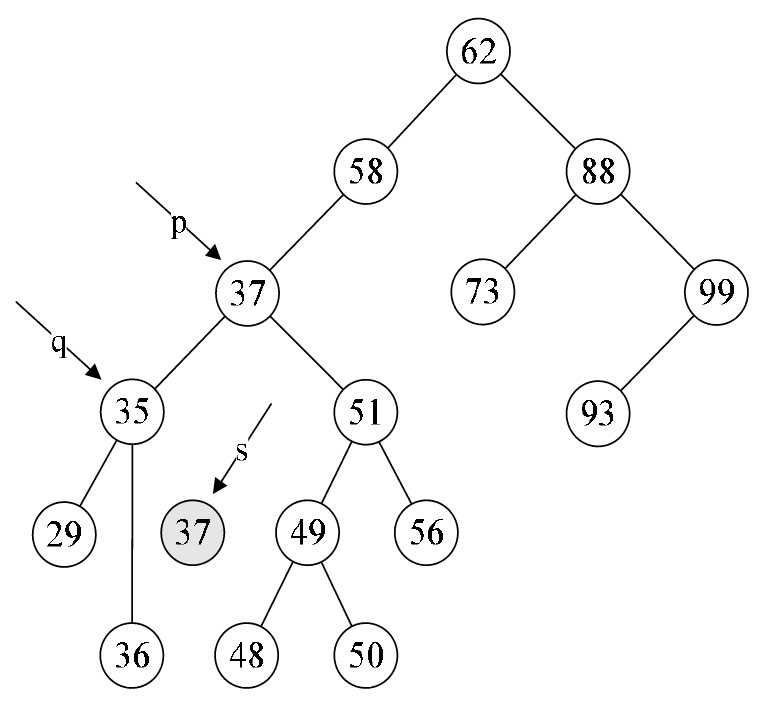
    1. 第24行，free(s)，就非常好理解了，将37结点删除，如图8-6-17所示。

    image.png

    从这段代码也可以看出，我们其实是在找删除结点的前驱结点替换的方法，对于用后继结点来替换，方法上是一样的。