对于无向图G=(V,{E})，如果边(v,v’)∈E，则称顶点v和v’互为邻接点（Adjacent），即v和v’相邻接。边(v,v’)依附（incident）于顶点v和v’，或者说(v,v’)与顶点v和v’相关联。顶点v的度（Degree）是和v相关联的边的数目，记为TD(v)。例如图7-2-8左侧上方的无向图，顶点A与B互为邻接点，边(A,B)依附于顶点A与B上，顶点A的度为3。而此图的边数是5，各个顶点度的和=3+2+3+2=10，推敲后发现，边数其实就是各顶点度数和的一半，多出的一半是因为重复两次记数。

    对于有向图G=(V,{E})，如果弧∈E，则称顶点v邻接到顶点v'，顶点v'邻接自顶点v。弧和顶点v，v’相关联。以顶点v为头的弧的数目称为v的入度（InDegree），记为ID(v)；以v为尾的弧的数目称为v的出度（OutDegree），记为OD(v)；顶点v的度为TD(v)=ID(v)+OD(v)。例如图7-2-8左侧下方的有向图，顶点A的入度是2（从B到A的弧，从C到A的弧），出度是1（从A到D的弧），所以顶点A的度为2+1=3。此有向图的弧有4条，而各顶点的出度和=1+2+1+0=4，各顶点的入度和=2+0+1+1=4。所以得到e=sigma(i=1, n, ID(v i ))=sigma(i=1, n, OD(v i ))。

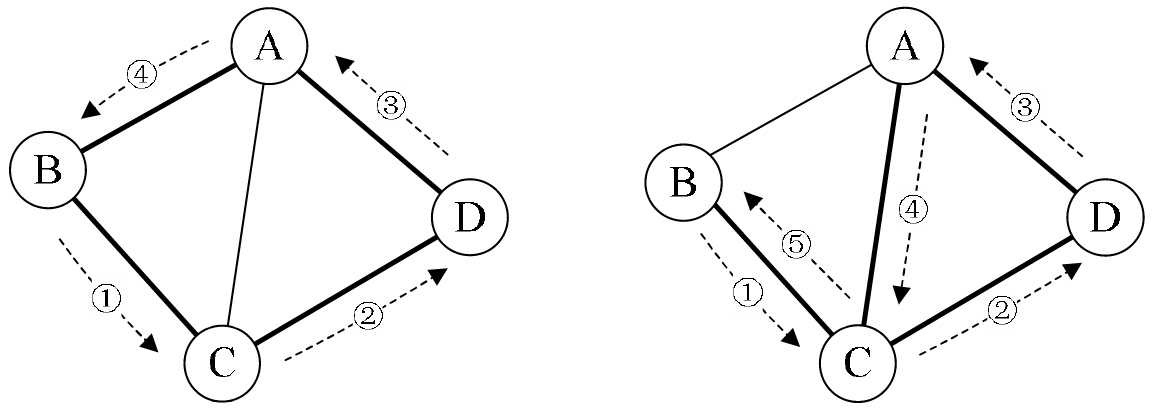
    无向图G=(V,{E})中从顶点v到顶点v’的路径（Path）是一个顶点序列(v=v i ,0,v i ,1,…,v i ,m=v’)，其中(v i ,j-1,v i ,j)∈E，1≤j≤m。例如图7-2-9中就列举了顶点B到顶点D四种不同的路径。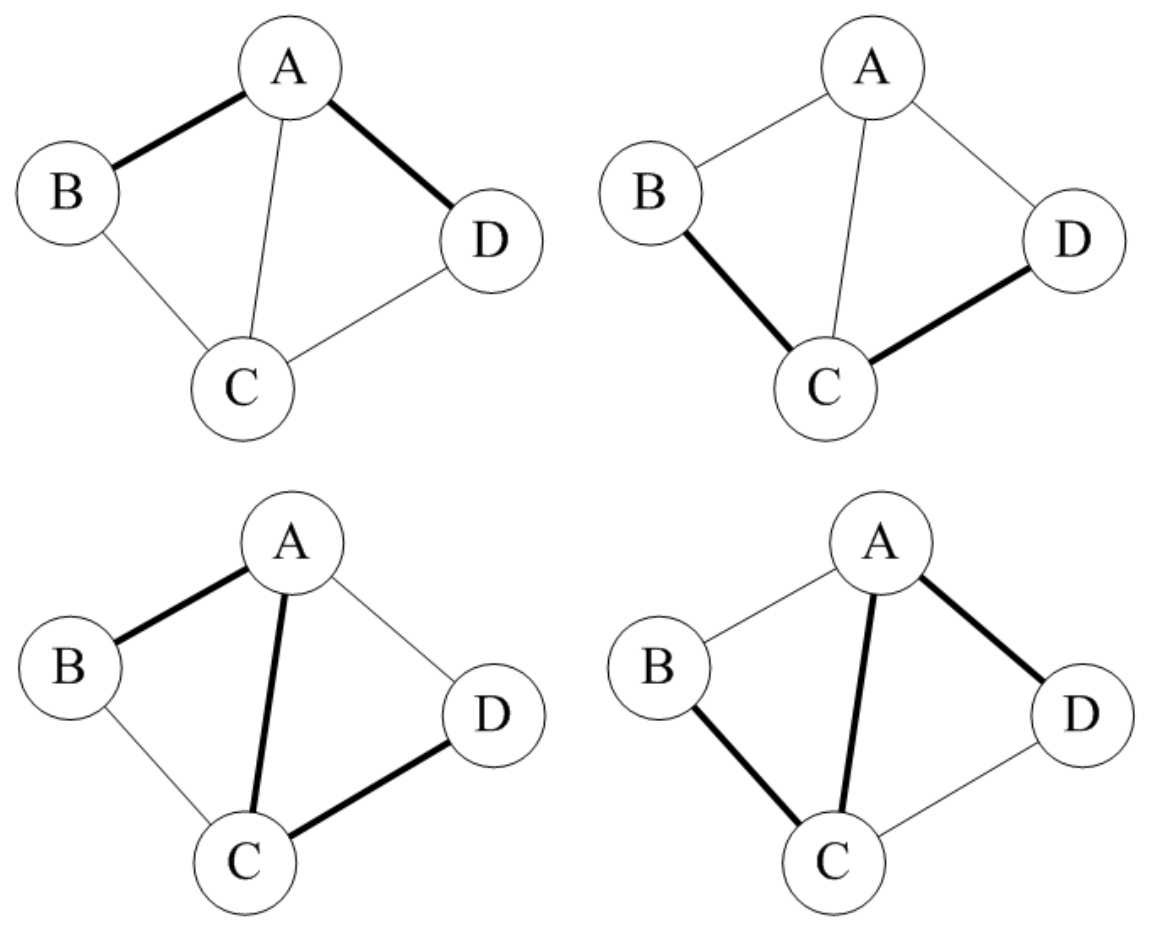
    image.png
    如果G是有向图，则路径也是有向的，顶点序列应满足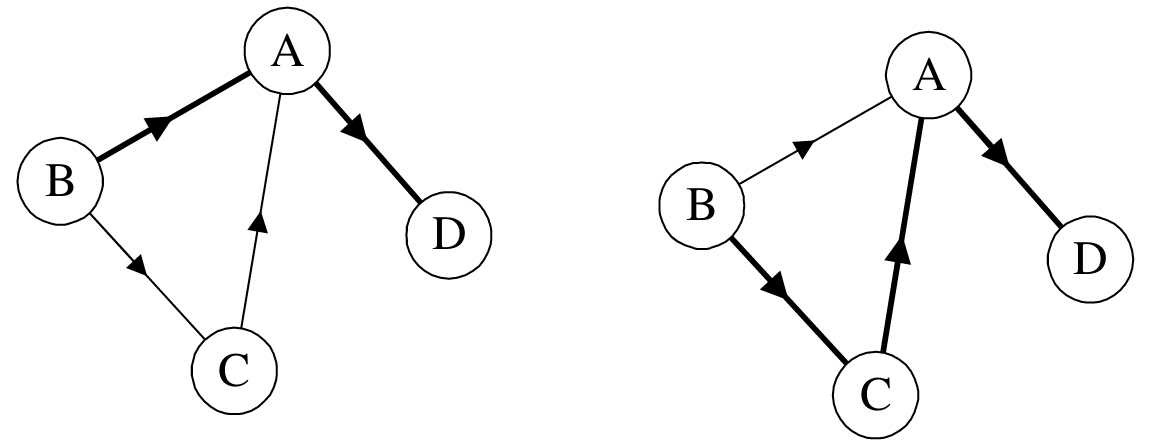∈E，1≤j≤m。例如图7-2-10，顶点B到D有两种路径。而顶点A到B，就不存在路径。
    image.png
    树中根结点到任意结点的路径是唯一的，但是图中顶点与顶点之间的路径却是不唯一的。

    路径的长度是路径上的边或弧的数目。图7-2-9中的上方两条路径长度为2，下方两条路径长度为3。图7-2-10左侧路径长为2，右侧路径长度为3。

    第一个顶点和最后一个顶点相同的路径称为回路或环（Cycle）。序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。图7-2-11中两个图的粗线都构成环，左侧的环因第一个顶点和最后一个顶点都是B，且C、D、A没有重复出现，因此是一个简单环。而右侧的环，由于顶点C的重复，它就不是简单环了。
    image.png