邻接矩阵是不错的一种图存储结构，但是我们也发现，对于边数相对顶点较少的图，这种结构是存在对存储空间的极大浪费的。比如说，如果我们要处理图7-4-5这样的稀疏有向图，邻接矩阵中除了arc[1][0]有权值外，没有其他弧，其实这些存储空间都浪费掉了。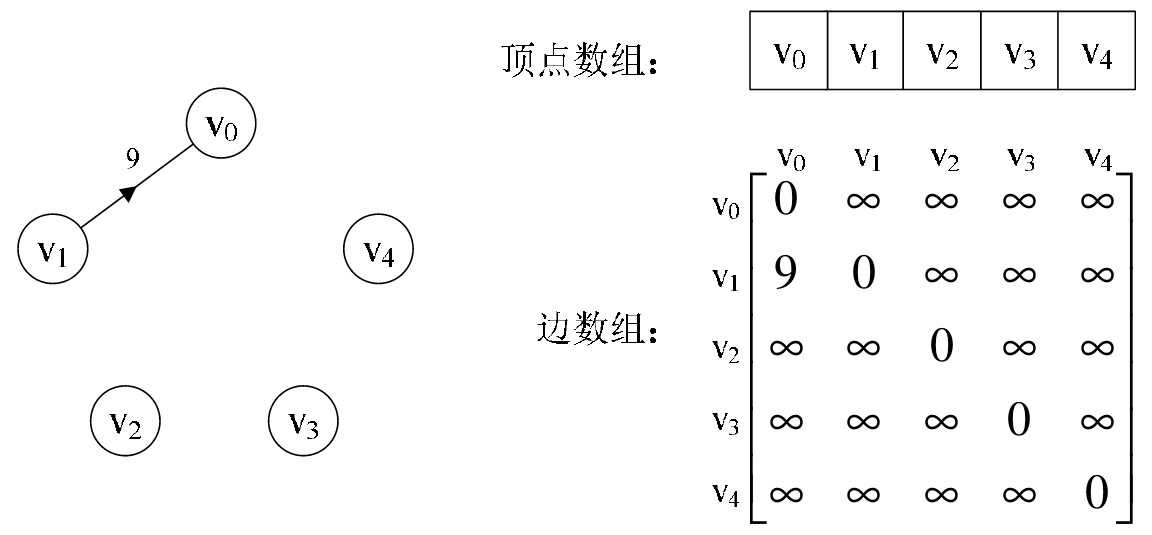
    image.png
    因此我们考虑另外一种存储结构方式。回忆我们在线性表时谈到，顺序存储结构就存在预先分配内存可能造成存储空间浪费的问题，于是引出了链式存储的结构。同样的，我们也可以考虑对边或弧使用链式存储的方式来避免空间浪费的问题。

    再回忆我们在树中谈存储结构时，讲到了一种孩子表示法，将结点存入数组，并对结点的孩子进行链式存储，不管有多少孩子，也不会存在空间浪费问题。这个思路同样适用于图的存储。我们把这种数组与链表相结合的存储方法称为邻接表（Adjacency List）。

    邻接表的处理办法是这样:

    1. 图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过数组可以较容易地读取顶点信息，更加方便。另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。
    2. 图中每个顶点v i 的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点v i 的边表，有向图则称为顶点v i 作为弧尾的出边表。

    例如图7-4-6所示的就是一个无向图的邻接表结构。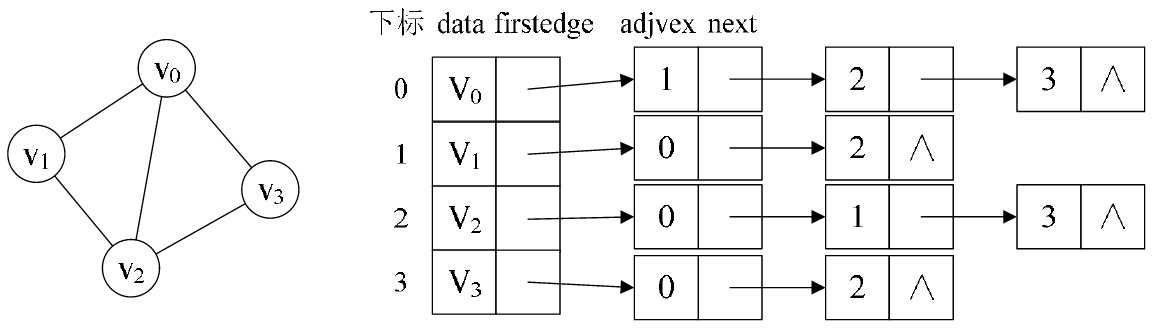
    image.png
    从图中我们知道，顶点表的各个结点由data和firstedge两个域表示，data是数据域，存储顶点的信息，firstedge是指针域，指向边表的第一个结点，即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标，next则存储指向边表中下一个结点的指针。比如v 1 顶点与v 0 、v 2 互为邻接点，则在v 1 的边表中，adjvex分别为v 0 的0和v 2 的2。

    这样的结构，对于我们要获得图的相关信息也是很方便的。比如我们要想知道某个顶点的度，就去查找这个顶点的边表中结点的个数。若要判断顶点v i 到v j 是否存在边，只需要测试顶点v i 的边表中adjvex是否存在结点v j 的下标j就行了。若求顶点的所有邻接点，其实就是对此顶点的边表进行遍历，得到的adjvex域对应的顶点就是邻接点。

    若是有向图，邻接表结构是类似的，比如图7-4-7中第一幅图的邻接表就是第二幅图。但要注意的是有向图由于有方向，我们是以顶点为弧尾来存储边表的，这样很容易就可以得到每个顶点的出度。但也有时为了便于确定顶点的入度或以顶点为弧头的弧，我们可以建立一个有向图的逆邻接表，即对每个顶点v i 都建立一个链接为v i 为弧头的表。如图7-4-7的第三幅图所示。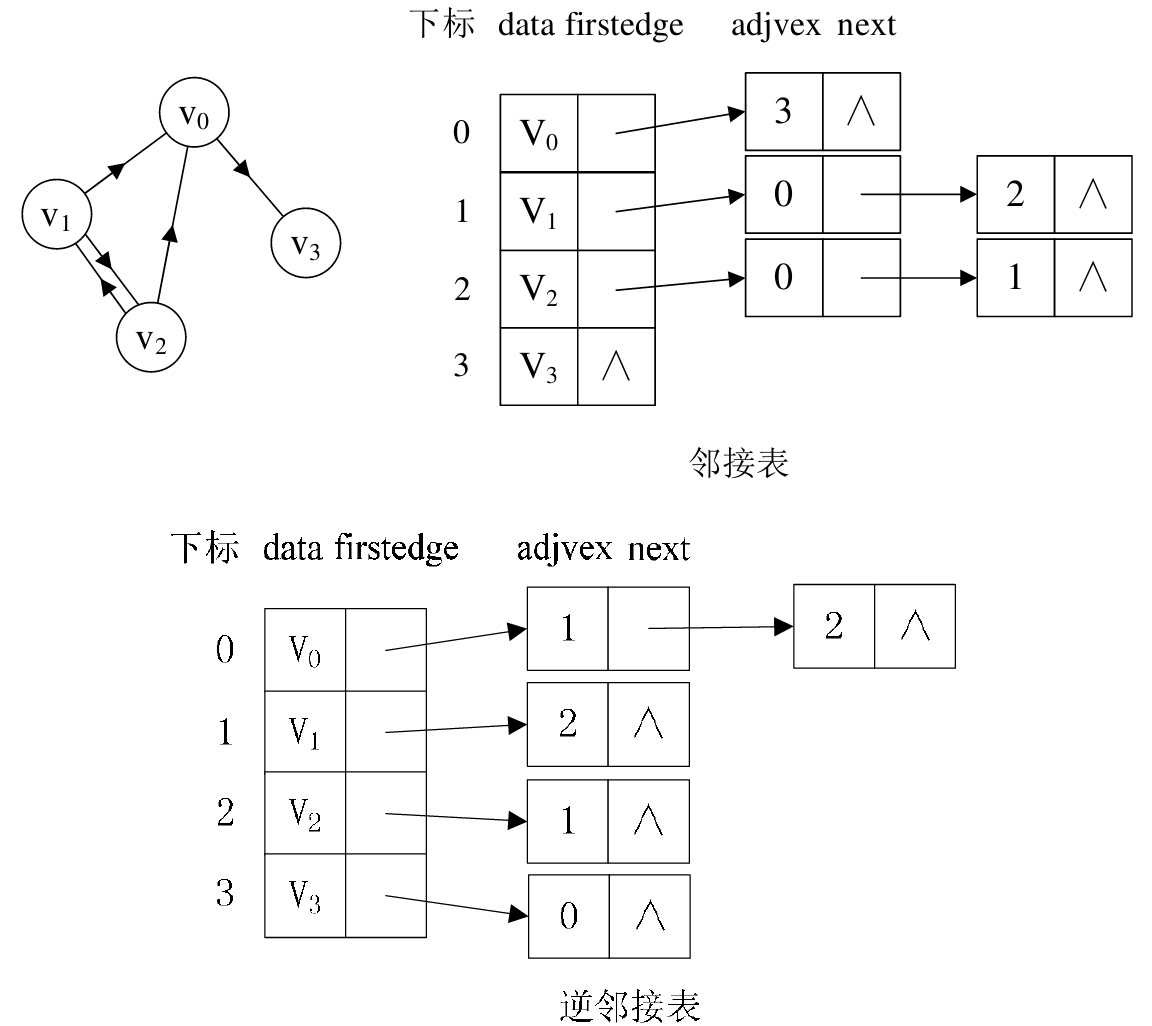
    image.png
    此时我们很容易就可以算出某个顶点的入度或出度是多少，判断两顶点是否存在弧也很容易实现。

    对于带权值的网图，可以在边表结点定义中再增加一个weight的数据域，存储权值信息即可，如图7-4-8所示。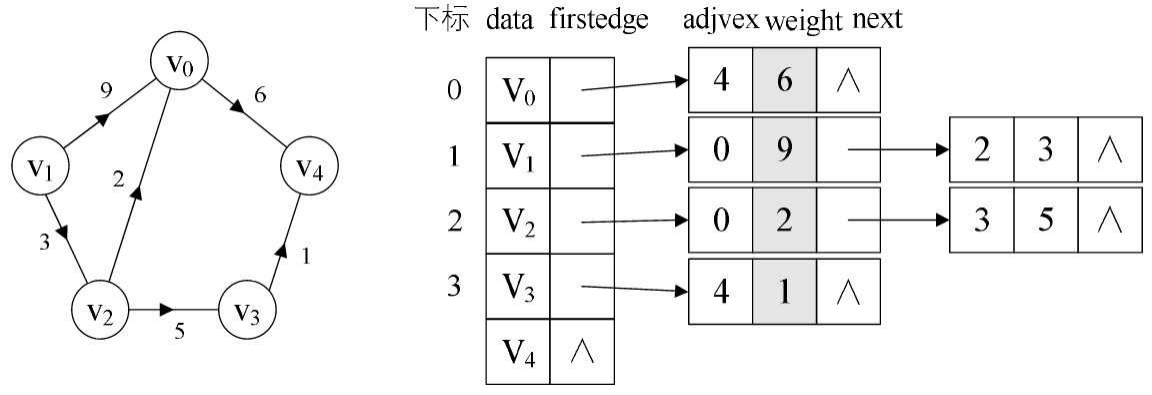
    image.png
    有了这些结构的图，下面关于结点定义的代码就很好理解了。

    1. /* 顶点类型应由用户定义 */
    2. typedef char VertexType;
    4. /* 边上的权值类型应由用户定义 */
    5. typedef int EdgeType;
    7. /* 边表结点 */
    8. typedef struct EdgeNode{
    10.     /* 邻接点域，存储该顶点对应的下标 */
    11.     int adjvex;
    13.     /* 用于存储权值，对于非网图可以不需要 */
    14.     EdgeType weight;
    16.     /* 链域，指向下一个邻接点　 */
    17.     struct EdgeNode *next;
    19. } EdgeNode;
    21. /* 顶点表结点 */
    22. typedef struct VertexNode{
    24.     /* 顶点域，存储顶点信息 */
    25.     VertexType data;
    27.     /* 边表头指针 */
    28.     EdgeNode *firstedge;
    30. } VertexNode, AdjList[MAXVEX];
    32. typedef struct{
    34.     AdjList adjList;
    36.     /* 图中当前顶点数和边数 */
    37.     int numVertexes, numEdges;
    39. } GraphAdjList;

    对于邻接表的创建，也就是顺理成章之事。无向图的邻接表创建代码如
    下。

    1. /* 建立图的邻接表结构 */
    2. void CreateALGraph(GraphAdjList *G){
    4.     int i, j, k;
    5.     EdgeNode *e;
    6.     printf("输入顶点数和边数:\n");
    8.     /* 输入顶点数和边数 */
    9.     scanf("%d,%d", &G->numVertexes,&G->numEdges);
    11.     /* 读入顶点信息，建立顶点表 */
    12.     for (i = 0; i < G->numVertexes; i++){
    14.         /* 输入顶点信息 */
    15.         scanf(&G->adjList[i].data);
    17.         /* 将边表置为空表 */
    18.         G->adjList[i].firstedge = NULL;
    20.     }
    22.     /* 建立边表 */
    23.     for (k = 0; k < G->numEdges; k++){
    25.         printf("输入边(vi,vj)上的顶点序号:\n");
    27.         /* 输入边(vi,vj)上的顶点序号 */
    28.         scanf("%d,%d", &i, &j);
    30.         /* 向内存申请空间，生成边表结点 */
    31.         e = (EdgeNode *)malloc(sizeof(EdgeNode));
    32.         /* 邻接序号为j */
    33.         e->adjvex = j;
    35.         /* 将e指针指向当前顶点指向的结点 */
    36.         e->next = G->adjList[i].firstedge;
    38.         /* 将当前顶点的指针指向e */
    39.         G->adjList[i].firstedge = e;
    41.         /* 向内存申请空间，生成边表结点 */
    42.         e = (EdgeNode *)malloc(sizeof(EdgeNode));
    44.         /* 邻接序号为i */
    45.         e->adjvex = i;
    47.         /* 将e指针指向当前顶点指向的结点 */
    48.         e->next = G->adjList[j].firstedge;
    50.         /* 将当前顶点的指针指向e */
    51.         G->adjList[j].firstedge = e;
    53.     } 
    55. }

    这里加粗代码，是应用了我们在单链表创建中讲解到的头插法，由于对于无向图，一条边对应都是两个顶点，所以在循环中，一次就针对i和j分别进行了插入。本算法的时间复杂度，对于n个顶点e条边来说，很容易得出是O(n+e)。