说如果兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。假设所有兔都不死，那么一年以后可以繁殖多少对兔子呢？

    我们拿新出生的一对小兔子分析一下：第一个月小兔子没有繁殖能力，所以还是一对；两个月后，生下一对小兔子数共有两对；三个月以后，老兔子又生下一对，因为小兔子还没有繁殖能力，所以一共是三对……依次类推可以列出下表。

    所经过的月数 1 2 3 4 5 6 7 8 9 10 11 12
    兔子对数 1 1 2 3 5 8 13 21 34 55 89 144

    表中数字1，1，2，3，5，8，13……构成了一个序列。这个数列有个十分明显的特点，那是：前面相邻两项之和，构成了后一项，如图4-8-2所示。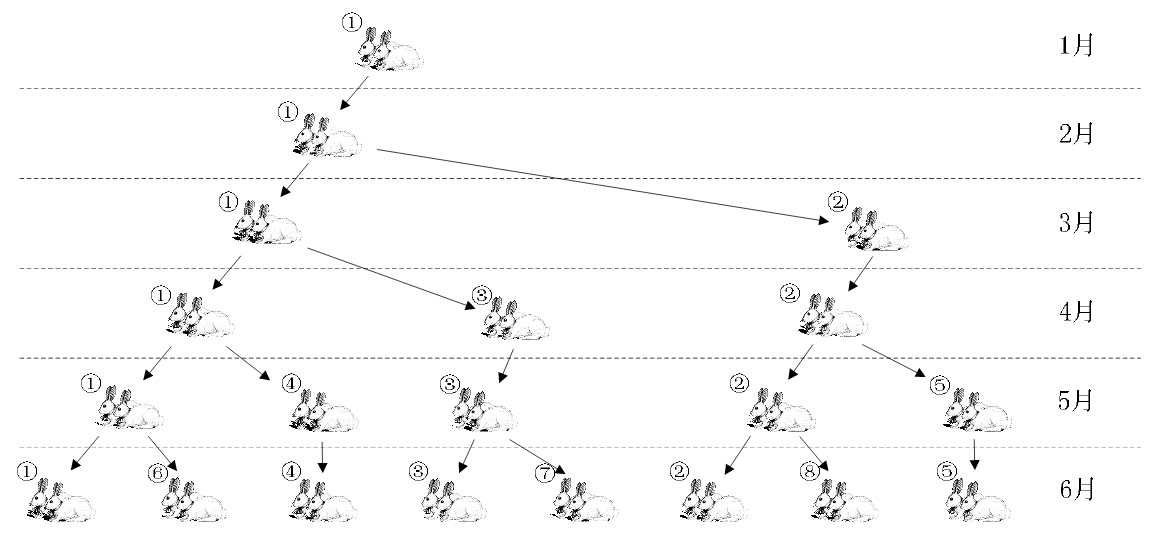
    image.png
    可以发现，编号①的一对兔子经过六个月就变成8对兔子了。如果我们
    用数学函数来定义就是：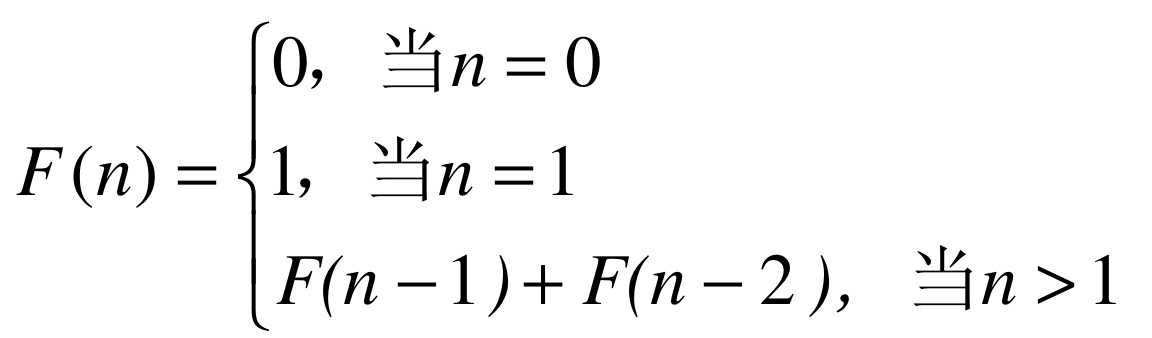
    image.png
    先考虑一下，如果我们要实现这样的数列用常规的迭代的办法如何实现？假设我们需要打印出前40位的斐波那契数列数。代码如下：

    1. int main(){
    3.     int i;
    4.     int a[40];
    6.     a[0] = 0;
    7.     a[1] = 1;
    9.     printf("%d ", a[0]);
    10.     printf("%d ", a[1]);
    12.     for (i = 2; i < 40; i++){
    14.         a[i] = a[i - 1] + a[i - 2];
    16.         printf("%d ", a[i]);
    18.     }
    20.     return 0;
    22. }

    代码很简单，几乎不用做什么解释。但其实我们的代码，如果用递归来实现，还可以更简单。

    1. /* 斐波那契的递归函数 */
    2. int Fbi(int i){
    4.     if (i < 2)
    5.         return i == 0 ? 0 : 1;
    7.     /* 这里Fbi就是函数自己，它在调用自己 */
    8.     return Fbi(i - 1) + Fbi(i - 2);
    10. }
    12. int main(){
    14.     int i;
    15.     for (i = 0; i < 40; i++)
    16.         printf("%d ", Fbi(i));
    18.     return 0;
    20. }

    怎么样，相比较迭代的代码，是不是干净很多。嘿嘿，不过要弄懂它得费点脑子。

    函数怎么可以自己调用自己？听起来有些难以理解，不过你可以不要把一个递归函数中调用自己的函数看作是在调用自己，而就当它是在调另一个函数。只不过，这个函数和自己长得一样而已。

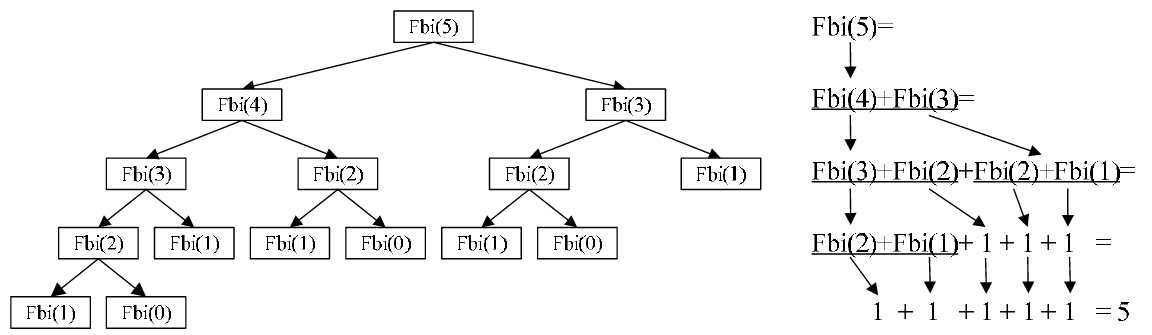
    我们来模拟代码中的Fbi(i)函数当i=5的执行过程，如图4-8-3所示。
    image.png