我们先把这两棵二叉树简化成叶子结点带权的二叉树(注:树结点间的边相关的数叫做权Weight),如图6-12-4所示。其中A表示不及格、B表示及格、C表示中等、D表示良好、E表示优秀。每个叶子的分支线上的数字就是刚才我们提到的五级分制的成绩所占百分比。
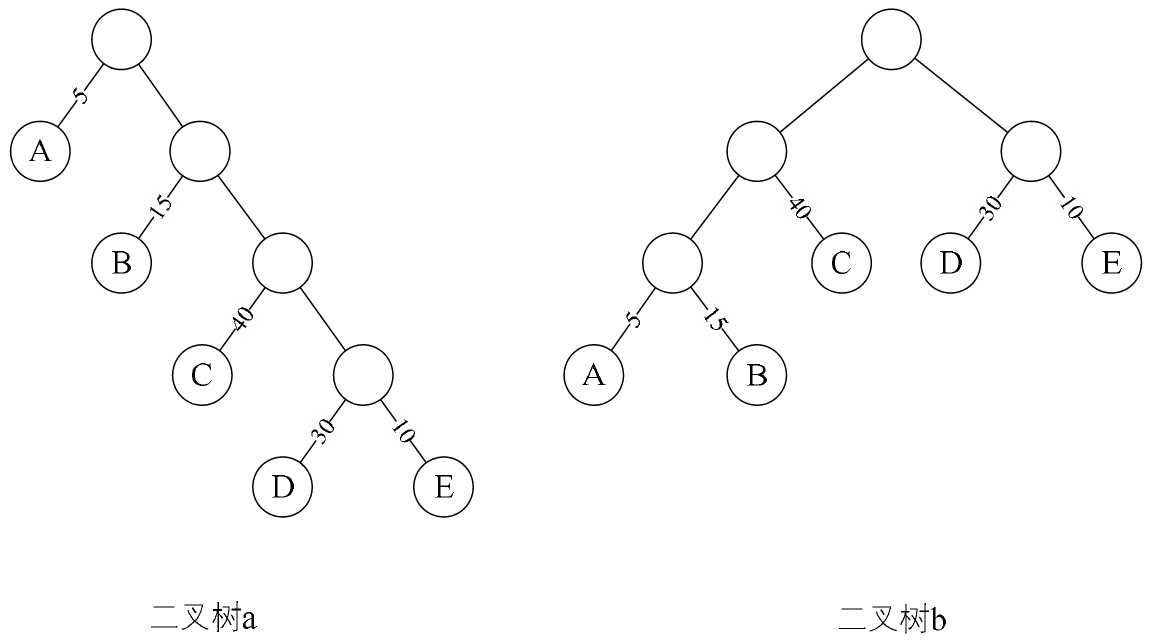
赫夫曼大叔说,从树中一个结点到另一个结点之间的分支构成两个结点之间的路径,路径上的分支数目称做路径长度。图6-12-4的二叉树a中,根结点到结点D的路径长度就为4,二叉树b中根结点到结点D的路径长度为2。树的路径长度就是从树根到每一结点的路径长度之和。二叉树a的树路径长度就为1+1+2+2+3+3+4+4=20。二叉树b的树路径长度就为1+2+3+3+2+1+2+2=16。
如果考虑到带权的结点,结点的带权的路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和。假设有n个权值{w 1 ,w 2 ,…,w n },构造一棵有n个叶子结点的二叉树,每个叶子结点带权w k ,每个叶子的路径长度为l k,我们通常记作,则其中带权路径长度WPL最小的二叉树称做赫夫曼树。
有了赫夫曼对带权路径长度的定义,我们来计算一下图6-12-4这两棵树的WPL值。
二叉树a的WPL=5×1+15×2+40×3+30×4+10×4=315
注意:这里5是A结点的权,1是A结点的路径长度,其他同理。
二叉树b的WPL=5×3+15×3+40×2+30×2+10×2=220
这样的结果意味着什么呢?如果我们现在有10000个学生的百分制成绩需要计算五级分制成绩,用二叉树a的判断方法,需要做31500次比较,而二叉树b的判断方法,只需要22000次比较,差不多少了三分之一量,在性能上提高不是一点点。
那么现在的问题就是,图6-12-4的二叉树b这样的树是如何构造出来的,这样的二叉树是不是就是最优的赫夫曼树呢?别急,赫夫曼大叔给了我们解决的办法。
- 先把有权值的叶子结点按照从小到大的顺序排列成一个有序序列,即:A5,E10,B15,D30,C40。
- 取头两个最小权值的结点作为一个新节点N 1 的两个子结点,注意相对较小的是左孩子,这里就是A为N 1 的左孩子,E为N 1 的右孩子,如图6-12-5所示。新结点的权值为两个叶子权值的和5+10=15。
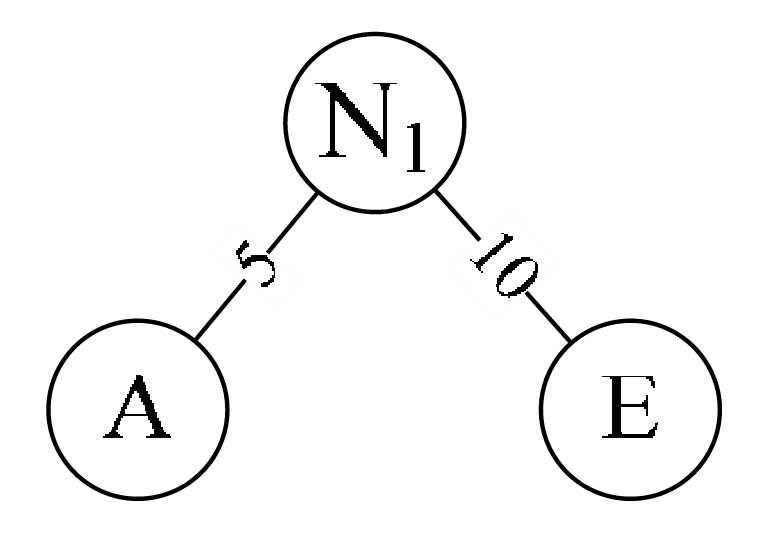
- 将N 1 替换A与E,插入有序序列中,保持从小到大排列。即:N 1 15,B 15,D 30,C 40。
- 重复步骤2。将N 1 与B作为一个新节点N 2 的两个子结点。如图6-12-6所示。N 2 的权值=15+15=30。
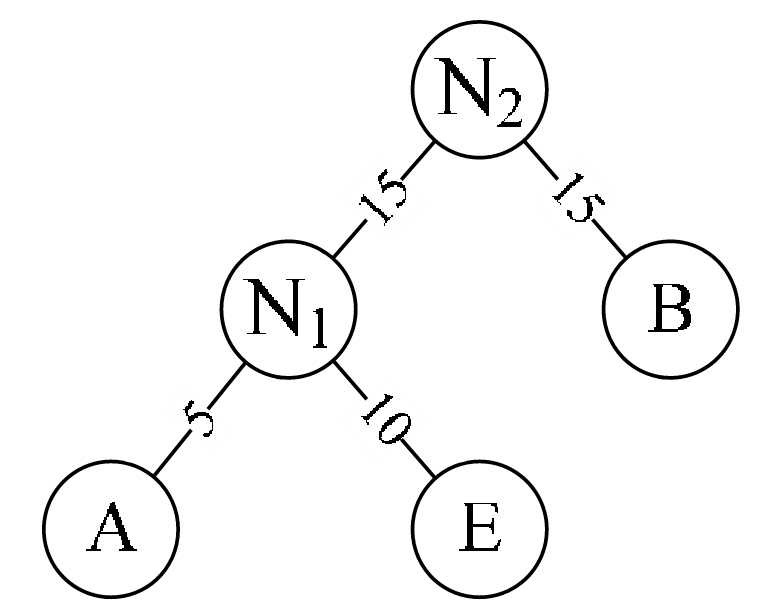
- 将N 2 替换N 1 与B,插入有序序列中,保持从小到大排列。即:N 2 30,D 30,C 40。
- 重复步骤2。将N 2 与D作为一个新节点N 3 的两个子结点。如图6-12-7所示。N 3 的权值=30+30=60。
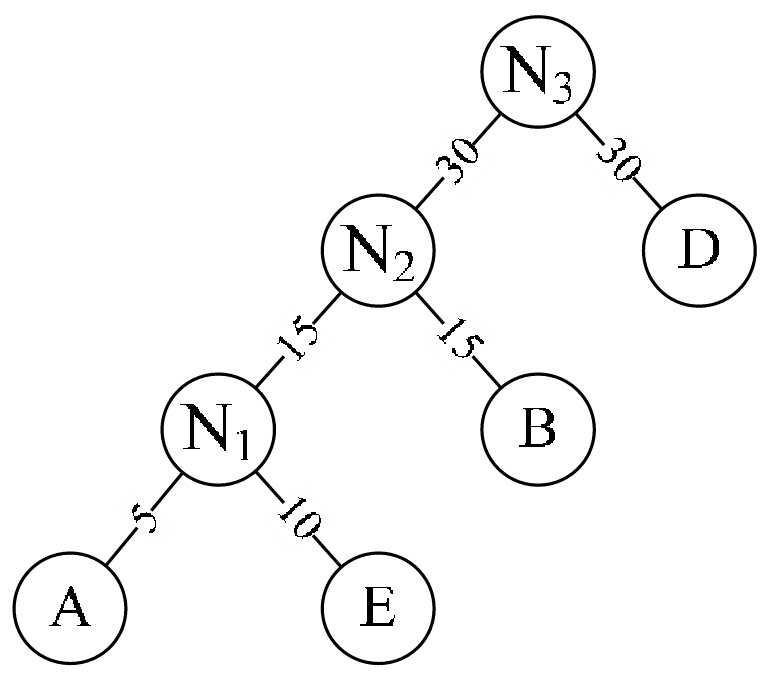
- 将N 3 替换N 2 与D,插入有序序列中,保持从小到大排列。即:C 40,N 3 60。
- 重复步骤2。将C与N3作为一个新节点T的两个子结点,如图6-12-8所示。由于T即是根结点,完成赫夫曼树的构造。
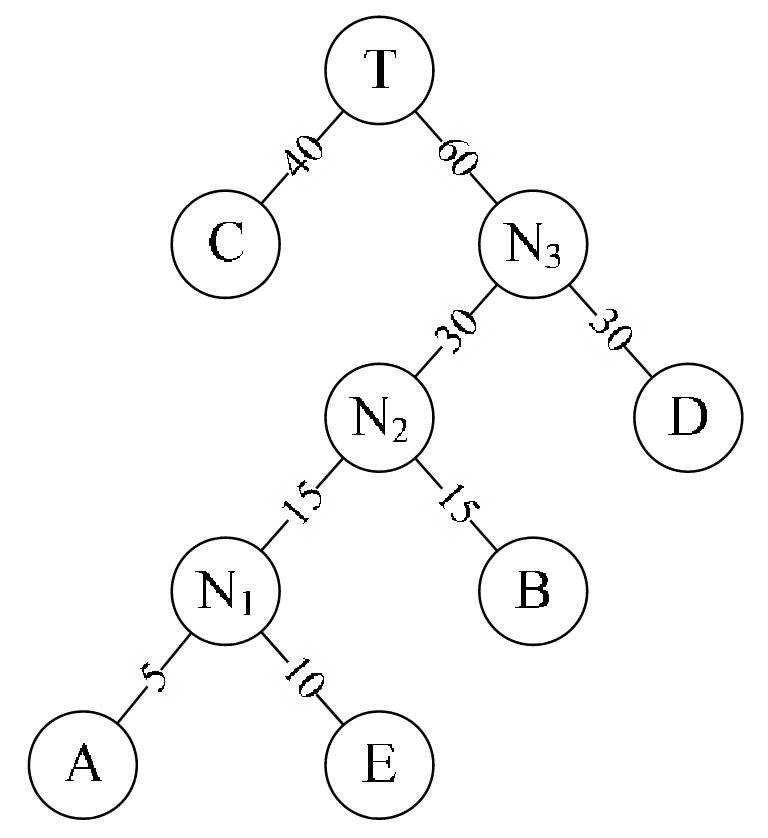
此时的图6-12-8二叉树的带权路径长度WPL=40×1+30×2+15×3+10×4+5×4=205。与图6-12-4的二叉树b的WPL值220相比,还少了15。显然此时构造出来的二叉树才是最优的赫夫曼树。
不过现实总是比理想要复杂得多,图6-12-8虽然是赫夫曼树,但由于每次判断都要两次比较(如根结点就是a<80&&a>=70,两次比较才能得到y或n的结果),所以总体性能上,反而不如图6-12-3的二叉树性能高。当然这并不是我们要讨论的重点了。
通过刚才的步骤,我们可以得出构造赫夫曼树的赫夫曼算法描述。
- 根据给定的n个权值{w 1 ,w 2 ,…,w n }构成n棵二叉树的集合F={T 1 ,T 2,…,T n },其中每棵二叉树T i 中只有一个带权为w i 根结点,其左右子树均为空。
- 在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
- 在F中删除这两棵树,同时将新得到的二叉树加入F中。
- 重复2和3步骤,直到F只含一棵树为止。
这棵树便是赫夫曼树。

