理解二进制交叉熵、对数损失函数:一种可视化解释

链接

介绍

如果您正在训练二进制分类器，则可能使用二进制交叉熵/对数损失作为损失函数。
你有没有想过使用这种损失函数究竟是什么意思？ 问题是，考虑到今天的库和框架的易用性，很容易忽略所使用的损失函数的真正含义。
动机
我正在寻找一篇博文，以一种视觉上清晰简洁的方式解释二进制交叉熵/对数损失背后的概念，所以我可以在Data Science Retreat向我的学生展示它。 由于我找不到任何符合我目的的东西，我自己负责编写任务:-)。
一个简单的分类问题
让我们从10个随机点开始：

x = [-2.2, -1.4, -0.8, 0.2, 0.4, 0.8, 1.2, 2.2, 2.9, 4.6]

这是我们唯一的特征：x。

现在，让我们为我们的点分配一些颜色：红色和绿色。 这些是我们的标签。

因此，我们的分类问题非常简单：鉴于我们的特征x，我们需要预测其标签：红色或绿色。

由于这是一个二元分类，我们也可以将这个问题描述为：“是点绿色”，或者更好的是，“点是绿色的概率是多少”？ 理想情况下，绿点的概率为1.0（绿色），而红点的概率为0.0（绿色）。

在此设置中，绿点属于正类（YES，它们是绿色），而红点属于负类（NO，它们不是绿色）。
如果我们拟合模型来执行此分类，它将预测每个点的绿色概率。 根据我们对点的颜色的了解，我们如何评估预测概率的优劣（或差）？ 这是损失功能的全部目的！ 它应该为错误预测返回高值，为良好预测返回低值。

对于像我们的例子那样的二进制分类，典型的损失函数是二进制交叉熵/对数损失函数。

损失函数：二进制交叉熵/对数损失函数

如果你观察这个损失函数，这就是你会发现的：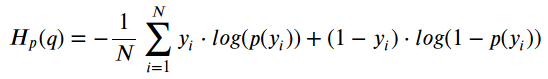

Binary Cross-Entropy / Log Loss
其中y是标签（绿点为1，红点为0），p(y)是所有N点的点为绿色的预测概率。

阅读这个公式，它告诉你，对于每个绿点（y = 1），它将log（p（y））添加到损失中，即它是绿色的对数概率。 相反，它为每个红点（y = 0）添加log（1-p（y）），即，它为红色的对数概率。 不一定很难，当然也不是那么直观……

此外，熵与这一切有什么关系？ 为什么我们首先记录概率？ 这些是有效的问题，我希望在下面的“给我看数学”部分回答它们。

计算损失-可视化方法

首先，让我们根据他们的类别（正面或负面）分割点数，如下图所示：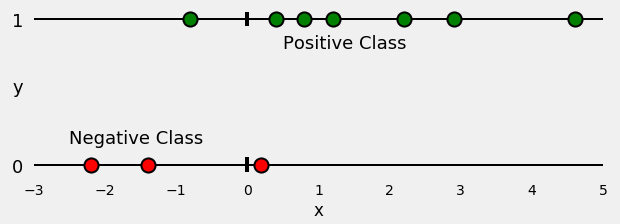

现在，让我们训练一个Logistic回归来对我们的点进行分类。 拟合回归是一个S形曲线，表示任何给定x点的绿色概率。 它看起来像这样：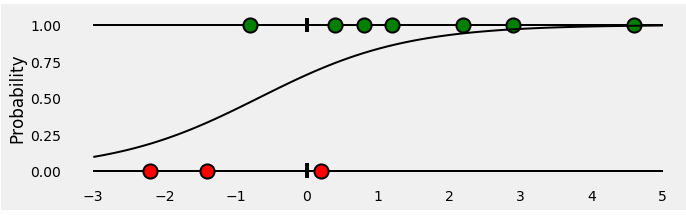

那么，对于属于正类（绿色）的所有点，我们的分类器给出的预测概率是多少？ 这些是S形曲线下的绿色条形，在与这些点对应的x坐标处。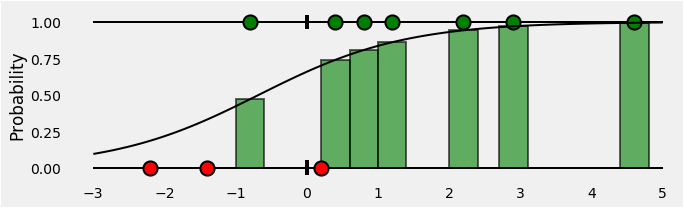

好的，到目前为止，真好！ 负面阶级的观点怎么样？ 请记住，S形曲线下的绿色条表示给定点为绿色的概率。 那么，给定点是红色的概率是多少？ 红色条在S形曲线上方，当然:-)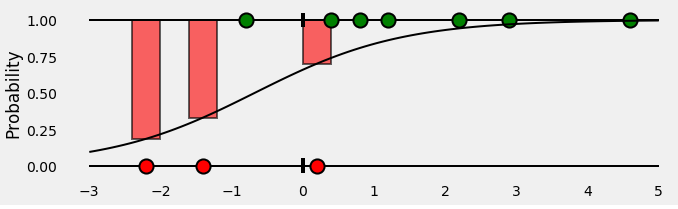

总而言之，我们最终会得到这样的结论：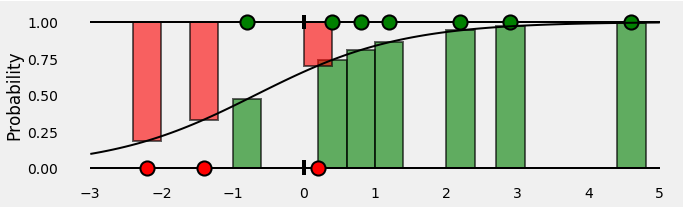

条形表示与每个点的相应真实类别相关联的预测概率！

好的，我们有预测的概率……通过计算二进制交叉熵/对数损失来评估它们的时间！

这些概率就是我们所需要的，所以，让我们摆脱x轴并将条带彼此相邻：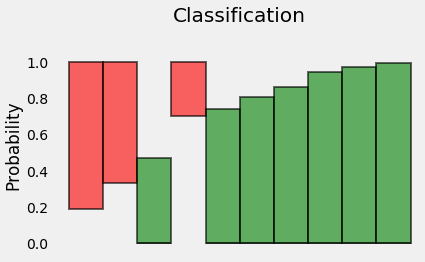

好吧，吊杆不再有意义了，所以让我们重新定位它们：

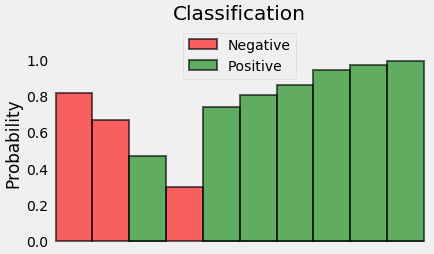
既然我们正试图计算损失，我们需要惩罚不好的预测，对吧？ 如果与真实类相关的概率为1.0，我们需要将其损失为零。 相反，如果这个概率很低，比如0.01，我们需要它的损失是巨大的！
事实证明，对于这个目的，取概率的（负）对数就足够了（因为0.0和1.0之间的值的对数是负的，我们采用负对数来获得损失的正值）。
实际上，我们使用日志的原因来自交叉熵的定义，请查看下面的“给我看数学”部分了解更多详情。
下图给出了一个清晰的图片 - 如果真实类的预测概率接近零，则损失呈指数增长：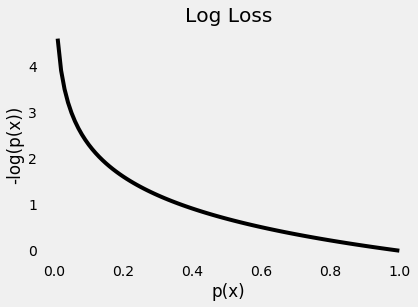

很公平！ 让我们采用概率的（负）对数 - 这些是每个点的相应损失。
最后，我们计算所有这些损失的平均值。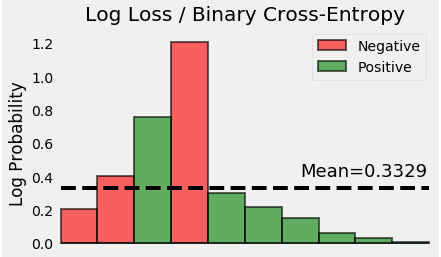

瞧！ 我们已经成功计算了这个玩具示例的二进制交叉熵/对数损失。 它是0.3329！
告诉我代码
如果你想仔细检查我们找到的值，只需运行下面的代码并亲自看看:-)

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import log_loss
import numpy as np
x = np.array([-2.2, -1.4, -.8, .2, .4, .8, 1.2, 2.2, 2.9, 4.6])
y = np.array([0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0])
logr = LogisticRegression(solver='lbfgs')
logr.fit(x.reshape(-1, 1), y)
y_pred = logr.predict_proba(x.reshape(-1, 1))[:, 1].ravel()
loss = log_loss(y, y_pred)
print('x = {}'.format(x))
print('y = {}'.format(y))
print('p(y) = {}'.format(np.round(y_pred, 2)))
print('Log Loss / Cross Entropy = {:.4f}'.format(loss))

告诉我数学（真的吗？！）
除了笑话之外，这篇文章并不打算在数学上倾向于……但是对于你们这些人，我的读者，想要了解熵的作用，所有这些中的对数，我们在这里:-)
如果你想深入了解信息理论，包括所有这些概念 - 熵，交叉熵等等 - 检查Chris Olah的帖子，它非常详细！

分布

让我们从分配点开始吧。 由于y表示我们的点的类（我们有3个红点和7个绿点），这就是它的分布，我们称之为q（y），如下所示：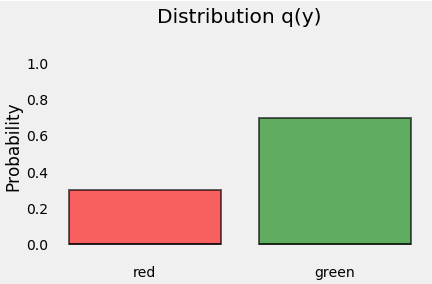

熵
熵是与给定分布q（y）相关的不确定性的度量。
如果我们所有的积分都是绿色怎么办 那个分布的不确定性是什么？ ZERO，对吗？ 毕竟，对于一个点的颜色毫无疑问：它总是绿色的！ 所以，熵是零！
另一方面，如果我们确切地知道一半的点是绿色而另一半点是红色的呢？ 那是最糟糕的情况，对吗？ 猜测点的颜色绝对没有优势：它完全是随机的！ 对于这种情况，熵由下面的公式给出（我们有两个类别（颜色） - 红色或绿色 - 因此，2）：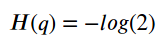

对于中间的其他情况，我们可以使用下面的公式计算分布的熵，如q（y），其中C是类的数量：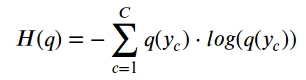

因此，如果我们知道随机变量的真实分布，我们就可以计算其熵。 但是，如果是这样的话，为什么首先要费心去训练分类器呢？ 毕竟，我们知道真正的分布……
但是，如果我们不这样做呢？ 我们可以尝试用其他一些分布近似真实分布，比如p（y）吗？ 我们当然可以！:-)

交叉熵

让我们假设我们的观点遵循其他分布p（y）。 但我们知道它们实际上来自真实（未知）分布q（y），对吧？
如果我们像这样计算熵，我们实际上是在计算两个分布之间的交叉熵：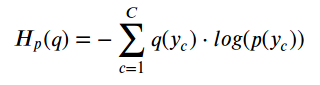

如果我们奇迹般地将p（y）与q（y）完美匹配，则交叉熵和熵的计算值也将匹配。
由于这可能永远不会发生，因此交叉熵将具有比在真实分布上计算的熵更大的BIGGER值。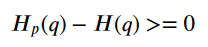

事实证明，交叉熵和熵之间的这个区别有一个名字……

Kullback-Leibler发散

Kullback-Leibler Divergence，简称“KL Divergence”，衡量两种发行版之间的差异：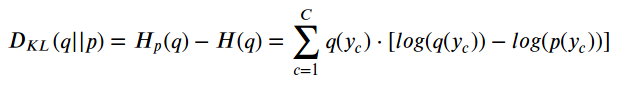

这意味着，p（y）越接近q（y），发散越低，因此交叉熵越低。
所以，我们需要找到一个好的p（y）来使用……但是，这是我们的分类器应该做的，不是吗？！ 确实如此！ 它寻找最好的p（y），这是最小化交叉熵的那个。

损失函数

在训练期间，分类器使用其训练集中的N个点中的每一个来计算交叉熵损失，有效地拟合分布p（y）！ 由于每个点的概率是1 / N，因此交叉熵由下式给出：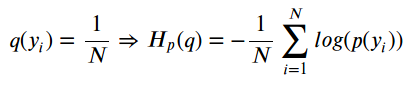

还记得上面的图6到10吗？ 我们需要在与每个点的真实类相关联的概率之上计算交叉熵。 这意味着使用绿色条形作为正类（y = 1）中的点，使用红色条形作为负类中的点（y = 0），或者数学上说：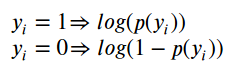

最后一步是计算两个类中所有点的平均值，正面和负面：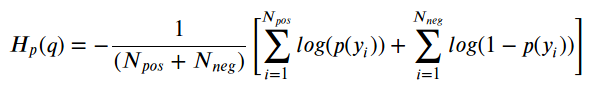

最后，通过一些操作，我们可以采用相同的公式，从正面或负面的类中获取任何一点：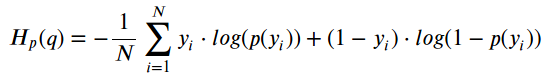

瞧！ 我们回到二进制交叉熵/日志丢失的原始公式:-)

最后的想法

我真的希望这篇文章能够对一个经常被认为理所当然的概念，即二元交叉熵作为损失函数的概念有所启发。 此外，我也希望它能够向您展示机器学习和信息理论如何联系在一起。