leetcode：84. 柱状图中最大的矩形

题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1：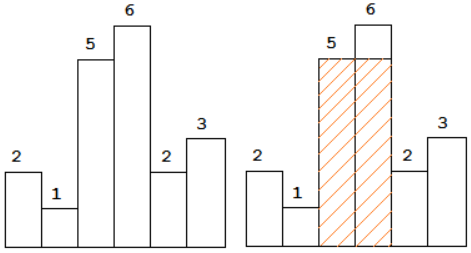
image.png

  1. 输入: [2,1,5,6,2,3]
  2. 输出: 10

示例 2：
[困难] 84. 柱状图中最大的矩形 - 图2

  1. 输入： heights = [2,4]
  2. 输出： 4

示例 3：
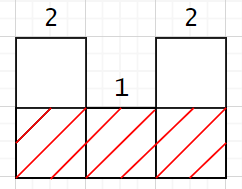
image.png

  1. 输入： heights = [2,1,2]
  2. 输出： 3

解答 & 代码

单调栈（栈中存储下标，下标对应的柱子高度严格单调递增）：

  1. 先借助单调栈，逆序遍历 heights 数组，求出每根柱子右边第一根比它矮的柱子的下标，存储在 rightLowerIdx
  2. 再借助单调栈，正序遍历 heights 数组，求出每根柱子左边第一根比它矮的柱子的下标，存储在 leftLowerIdx
  3. 最后再遍历 heights 数组，分别以每根柱子高度 heights[i] 作为矩形高度，那么 rightLowerIdx[i] - leftLowerIdx[i] - 1 就是这个高度能向两边拓展的最大宽度，计算得到一个矩形面积 curArea，如果大于全局最大矩形面积 maxArea，则更新 maxArea

  4. 返回 maxArea

    1. class Solution {
    2. public:
    3.  int largestRectangleArea(vector<int>& heights) {
    4.      int len = heights.size();
    5.        // 1. 先借助单调栈，逆序遍历 heights 数组，求出每根柱子右边第一根比它矮的柱子的下标，
    6.        // 存储在 rightLowerIdx
    7.      vector<int> rightLowerIdx(len, -1);
    8.      stack<int> s;        // 单调栈
    9.      for(int i = len - 1; i >= 0; --i)
    10.      {
    11.          while(!s.empty() && heights[s.top()] >= heights[i])
    12.              s.pop();
    13.          rightLowerIdx[i] = s.empty() ? len : s.top();
    14.          s.push(i);
    15.      }
    17.        // 2. 再借助单调栈，正序遍历 heights 数组，求出每根柱子左边第一根比它矮的柱子的下标，
    18.        // 存储在 leftLowerIdx
    19.      vector<int> leftLowerIdx(len, -1);
    20.      while(!s.empty())
    21.          s.pop();
    22.      for(int i = 0; i < len; ++i)
    23.      {
    24.          while(!s.empty() && heights[s.top()] >= heights[i])
    25.              s.pop();
    26.          leftLowerIdx[i] = s.empty() ? -1 : s.top();
    27.          s.push(i);
    28.      }
    30.        // 3. 最后再遍历 heights 数组，分别以每根柱子高度 heights[i] 作为矩形高度，
    31.        // 那么 rightLowerIdx[i] - leftLowerIdx[i] - 1 就是这个高度能向两边拓展的最大宽度，
    32.        // 计算得到一个矩形面积 curArea，如果大于全局最大矩形面积 maxArea，则更新 maxArea
    33.      int maxArea = 0;    // 柱状图中最大矩形面积
    34.      for(int i = 0; i < len; ++i)
    35.      {
    36.          int curArea = heights[i] * (rightLowerIdx[i] - leftLowerIdx[i] - 1);
    37.          maxArea = max(maxArea, curArea);
    38.      }
    39.      return maxArea;
    40.  }
    41. };

    复杂度分析：设 heights 数组长度为 N

  • 时间复杂度 O(N)：三次遍历数组
  • 空间复杂度 O(N)：两个数组 rightLowerIdx、leftLowerIdx 长度都为 N，单调栈 s 中最多同时存储 N 个数

执行结果：

  1. 执行结果：通过
  3. 执行用时：144 ms, 在所有 C++ 提交中击败了 12.72% 的用户
  4. 内存消耗：79.4 MB, 在所有 C++ 提交中击败了 5.01% 的用户