leetcode：142. 环形链表 II

题目

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
不允许修改 链表。

示例 1：
[中等] 142. 环形链表 II - 图1

  1. 输入：head = [3,2,0,-4], pos = 1
  2. 输出：返回索引为 1 的链表节点
  3. 解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：
[中等] 142. 环形链表 II - 图2

  1. 输入：head = [1,2], pos = 0
  2. 输出：返回索引为 0 的链表节点
  3. 解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

[中等] 142. 环形链表 II - 图3

  1. 输入：head = [1], pos = -1
  2. 输出：返回 null
  3. 解释：链表中没有环。

解答 & 代码

快慢指针：

  1. 先判断链表是否有环（快指针一次走两步，慢指针一次走一步，直到相遇）
  2. 寻找入环节点：快指针回到链表头节点，两个指针同时走，一次走一步，再次相遇的地方就是入环节点

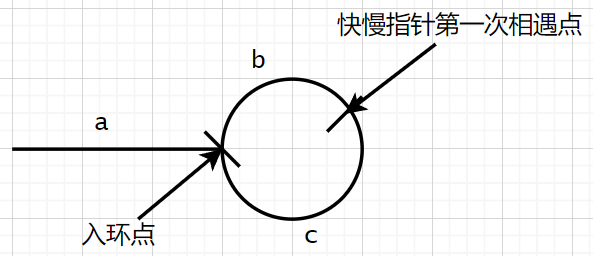
image.png

  • a + m(b + c) + b = 2(a + n(b + c) +b)
    • 快慢指针第一次相遇时，快指针走过的路程时慢指针走过路程的 2 倍

  • → a = (m - 2n)(b + c) - b

    • 快指针回到链表头节点，慢指针从第一次相遇点继续出发，每次都走一步，快指针走到入环点的距离 a = (m - 2n)(b + c) - b，慢指针也走了那么远，刚好是在入环点

      1. /**
      2. * Definition for singly-linked list.
      3. * struct ListNode {
      4. *     int val;
      5. *     ListNode *next;
      6. *     ListNode(int x) : val(x), next(NULL) {}
      7. * };
      8. */
      9. class Solution {
      10. public:
      11. ListNode *detectCycle(ListNode *head) {
      12.    ListNode* fast = head;    // 快指针
      13.    ListNode* slow = head;    // 慢指针
      14.    // 1. 先判断链表是否有环
      15.    while(fast != NULL && fast->next != NULL)
      16.    {
      17.        fast = fast->next->next;    // 快指针走两步
      18.        slow = slow->next;            // 慢指针走一步
      19.        // 快慢指针相遇，说明链表存在环
      20.        if(fast == slow)        
      21.            break;
      22.    }
      23.    // fast 走到链表尾部，说明链表中无环，直接返回 NULL
      24.    if(fast == NULL || fast->next == NULL)
      25.        return NULL;
      27.    // 2. 寻找入环节点
      28.    fast = head;    // 快指针回到链表头节点
      29.    // 快慢指针每次都走一步，直到相遇
      30.    while(fast != slow)
      31.    {
      32.        fast = fast->next;
      33.        slow = slow->next;
      34.    }
      35.    return fast;    // 相遇的节点就是入环节点
      36. }
      37. };

      复杂度分析：设链表节点数 N

  • 时间复杂度 O(N)：第一步判断两个链表是否有环（即判断快慢指针是否相遇）时，慢指针走过的距离不会超过链表总长度 N；第二步寻找入环节点慢指针走过的距离是入环前的这一段，也小于 N

  • 空间复杂度 O(1)

执行结果：

  1. 执行结果：通过
  3. 执行用时：4 ms, 在所有 C++ 提交中击败了 98.16% 的用户
  4. 内存消耗：7.5 MB, 在所有 C++ 提交中击败了 43.18% 的用户

拓展题

[中等] 287. 寻找重复数