题目

给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。
由于答案可能很大，因此 返回答案模 10^9 + 7 。

示例：

输入：arr = [3,1,2,4]
输出：17
解释：
子数组为 [3]，[1]，[2]，[4]，[3,1]，[1,2]，[2,4]，[3,1,2]，[1,2,4]，[3,1,2,4]。 
最小值为 3，1，2，4，1，1，2，1，1，1，和为 17。

输入：arr = [11,81,94,43,3]
输出：444

解答 & 代码

单调栈：本题思路同[困难] 84. 柱状图中最大的矩形

借助单调栈，求每个元素 arr[i] 左边严格比 **arr[i]** 小的最近的元素的位置，存储在 left 数组
借助单调栈，求每个元素 arr[i] 右边非严格比 **arr[i]** 小的最近元素的位置，存储在 right 数组

非严格比 arr[i] 小，指的是小于等于 **arr[i]** 的元素的位置
因为，如果左、右两边都取严格比 arr[i] 小的元素位置，那么后面第三步统计的时候，会出现一些子数组被重复统计两次
eg. 如下图所示，会重复统计。因此必须一边取严格小，一边取非严格小

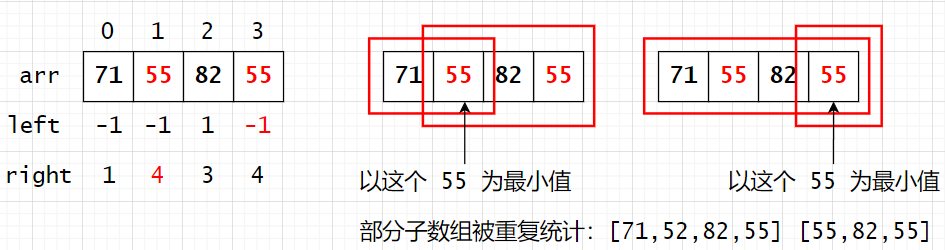
遍历 arr 数组，分别以每个元素 **arr[i]** 为最小值，统计以 arr[i] 为最小值的的子数组的个数 **= (i - left[i]) * (right[i] - i)**，乘上最小值 arr[i]，加到 result

class Solution {
public:
 int sumSubarrayMins(vector<int>& arr) {
     int len = arr.size();
     // 1. 借助单调栈，求每个元素 arr[i] 左边严格比 arr[i] 小的最近的元素的位置，存储在 left 数组
     vector<int> left(len);
     stack<int> s;
     for(int i = 0; i < len; ++i)
     {
         while(!s.empty() && arr[s.top()] >= arr[i])
             s.pop();
         left[i] = s.empty() ? -1 : s.top();
         s.push(i);
     }

     // 2. 借助单调栈，求每个元素 arr[i] 右边非严格比 arr[i] 小的最近元素的位置，存储在 right 数组
     // 非严格比 arr[i] 小，指的是小于等于 arr[i] 的元素
     vector<int> right(len);
     while(!s.empty())
         s.pop();
     for(int i = len - 1; i >= 0; --i)
     {
         while(!s.empty() && arr[s.top()] > arr[i])
             s.pop();
         right[i] = s.empty() ? len : s.top();
         s.push(i);
     }

     // 3. 遍历 arr 数组，计算以每个元素 arr[i] 为最小值的子数组的个数，乘上 arr[i]，加到 result 
     long long result = 0;
     int MOD = 1e9 + 7;
     for(int i = 0; i < len; ++i)
     {
         result += (((long long)(i - left[i]) * (right[i] - i) % MOD) * arr[i]) % MOD;
         result %= MOD;
     }

     return result;
 }
};

复杂度分析：设数组长为 n

时间复杂度 O(n)：
空间复杂度 O(n)：

执行结果：

执行结果：通过

执行用时：80 ms, 在所有 C++ 提交中击败了 51.73% 的用户
内存消耗：41.9 MB, 在所有 C++ 提交中击败了 24.39% 的用户

hot 100

[中等] 907. 子数组的最小值之和

题目

解答 & 代码