leetcode：1059. 从始点到终点的所有路径

题目

给定有向图的边 edges，以及该图的始点 source 和目标终点 destination，确定从始点 source 出发的所有路径是否最终结束于目标终点 destination，即：

  • 从始点 source 到目标终点 destination 存在至少一条路径
  • 如果存在从始点 source 到没有出边的节点的路径，则该节点就是路径终点。
  • 从始点 source 到目标终点 destination 可能路径数是有限数字

当从始点 source 出发的所有路径都可以到达目标终点 destination 时返回 true，否则返回 false。

示例 1：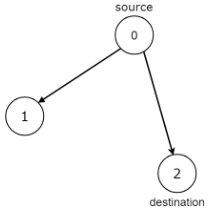
image.png

  1. 输入：n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
  2. 输出：false
  3. 说明：会卡在 节点 1，到不了目标终点节点 2。

示例 2：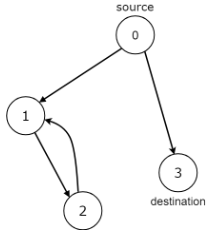
image.png

输入：n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
输出：false
说明：有两种可能：在节点 3 处结束，或是在节点 1 和节点 2 之间无限循环。

示例 3：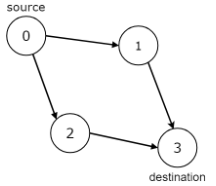
image.png

输入：n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
输出：true

示例 4：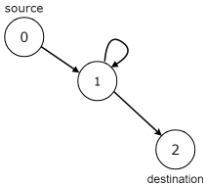
image.png

输入：n = 3, edges = [[0,1],[1,1],[1,2]], source = 0, destination = 2
输出：false
说明：从始点出发的所有路径都在目标终点结束，
但存在无限多的路径，如 0-1-2，0-1-1-2，0-1-1-1-2，0-1-1-1-1-2 等。

示例 5：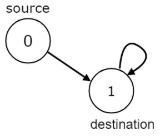
image.png

输入：n = 2, edges = [[0,1],[1,1]], source = 0, destination = 1
输出：false
说明：在目标节点上存在无限的自环。

解答 & 代码

递归回溯

#include <iostream>
#include <vector>
using namespace std;

// 递归回溯
bool backTrace(vector<vector<int>> graph, vector<bool> visited, int cur, int destination)
{
    // 递归结束条件：如果走到路径终点，若当前节点就是目标终点，则返回 true，否则返回 false
    if(graph[cur].size() == 0)
        return cur == destination;

    // 遍历当前节点所有可达的后继节点
    for(int i = 0; i < graph[cur].size(); ++i)
    {
        int next = graph[cur][i];
        // 如果该后继结点被访问过，说明这条路径存在环，因此存在无限多条路径，直接返回 false
        if(visited[next] == true)
            return false;
        // 选择；将该后继节点标为已访问
        visited[next] = true;
        // 递归回溯，如果结果为 false，则直接返回 false
        if(backTrace(graph, visited, next, destination) == false)
            return false;
        // 撤销选择：将该后继节点重新标为未访问
        visited[next] = false;
    }

    return true;
}

int main()
{
    int n = 2;                  // 节点数
    vector<vector<int>> edges = {{0, 1}, {1, 1}};   // 边
    int source = 0;             // 起点
    int destination = 1;        // 终点

    vector<vector<int>> graph(n);
    for(int i = 0; i < edges.size(); ++i)
        graph[edges[i][0]].push_back(edges[i][1]);

    bool result;
    // 如果目标终点后面还有后继节点，则直接返回 false
    if(!graph[destination].empty())
        result = false;

    vector<bool> visited(n, false);
    result = backTrace(graph, visited, source, destination);
    if(result == true)
        cout << "true" << endl;
    else
        cout << "false" << endl;

    return 0;
}