leetcode：124. 二叉树中的最大路径和

题目

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：
[困难] 124. 二叉树中的最大路径和 - 图1

  1. 输入：root = [1,2,3]
  2. 输出：6
  3. 解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：
[困难] 124. 二叉树中的最大路径和 - 图2

  1. 输入：root = [-10,9,20,null,null,15,7]
  2. 输出：42
  3. 解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

解答 & 代码

递归计算二叉树每个节点的最大贡献值 **nodeMaxGain()**（即以该节点为根节点的子树中，以该节点为起点的、节点值之和最大的路径，这条最大路径上的各节点值之和就是最大贡献值），计算步骤如下：

  1. 递归结束条件：如果当前节点为空，则对应的最大贡献值为 0，返回 0
  2. 递归计算左孩子节点的最大贡献值（若小于 0，则取 0，表示不选取左孩子节点）
  3. 递归计算右孩子节点的最大贡献值（若小于 0，则取 0，表示不选取右孩子节点）
  4. 计算当前节点的最大贡献值 = 当前节点的值 + 左/右孩子节点的最大贡献值的较大值，并返回

上面计算的每个节点的最大贡献值是以该节点为起点向某个子树方向延伸的路径对应的节点值之和，但对于以该节点为根的子树，并且要求经过该节点的路径中，最大路径和还要加上另一个未使用的孩子节点的贡献值，即最大路径和 = 左孩子节点的最大贡献值 + 当前节点的值 + 右孩子节点的最大贡献值

使用一个变量 maxSum 代表最大路径和，在上述 3、4 步之间插入一步求当前最大路径和（以该节点为根的子树中，并且要求经过该节点的路径中和最大的路径），若当前最大路径和 > maxSum，则更新 maxSum \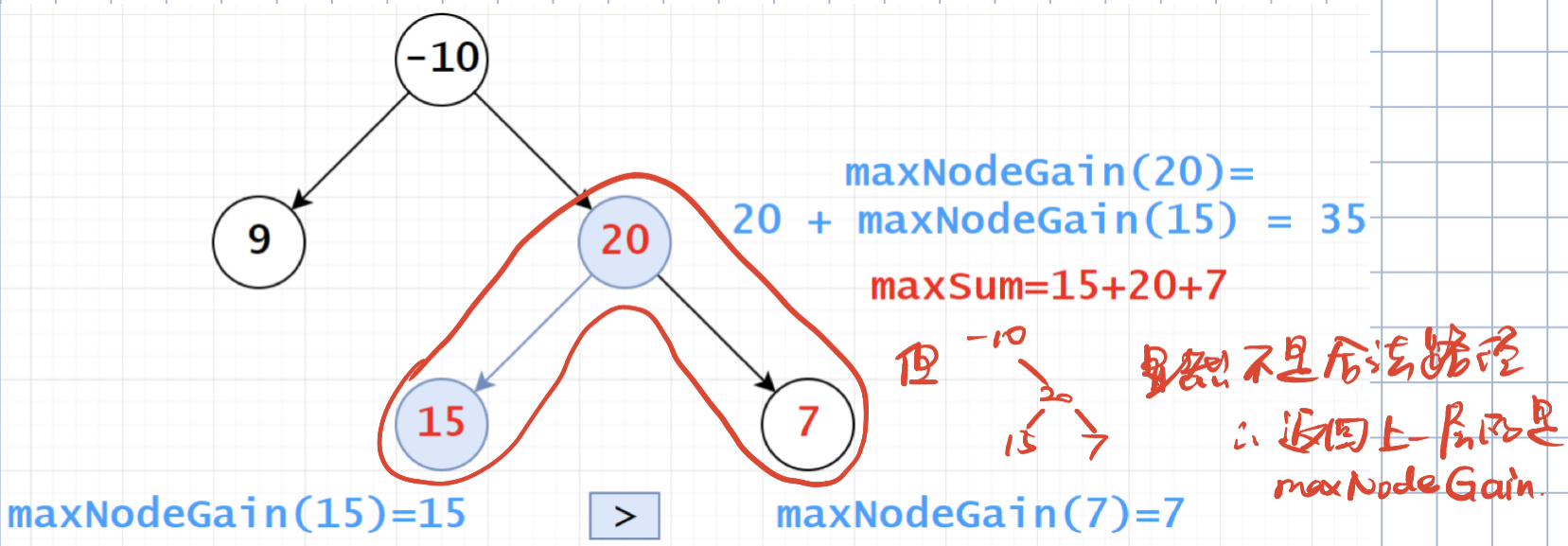
IMG_6932(20210716-150815).PNG
总结：核心在于计算结果的时候要计算左右子树，但递归返回的时候只能返回较大的一边

  1. /**
  2.  * Definition for a binary tree node.
  3.  * struct TreeNode {
  4.  *     int val;
  5.  *     TreeNode *left;
  6.  *     TreeNode *right;
  7.  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  8.  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  9.  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  10.  * };
  11.  */
  12. class Solution {
  13. private:
  14.     int result = INT_MIN;    // 结果，二叉树的最大路径和
  15.     /* 递归函数定义：输入根节点 root，返回该二叉树的高度。且要在后序位置更新二叉树的最大路径和 */
  16.     int dfsHeight(TreeNode* root)
  17.     {
  18.         if(root == nullptr)
  19.             return 0;
  21.         // 递归计算左/右子节点的最大贡献值
  22.         // 如果左/右子节点的最大贡献值小于 0，则不会选取左/右子节点，因此和 0 取 max
  23.         int leftHeight = max(dfsHeight(root->left), 0);
  24.         int rightHeight = max(dfsHeight(root->right), 0);
  26.         // 包含当前节点的最大路径和 = 左节点的最大贡献值 + 当前节点值 + 右节点的最大贡献值
  27.         int maxCurPathSum = leftHeight + root->val + rightHeight;
  28.         // 更新最大路径和
  29.         result = max(result, maxCurPathSum);
  31.         // 返回当前节点的最大贡献值
  32.         return max(leftHeight, rightHeight) + root->val;
  33.     }
  34. public:
  35.     int maxPathSum(TreeNode* root) {
  36.         dfsHeight(root);
  37.         return result;
  38.     }
  39. };

复杂度分析：设二叉树节点数为 N

  • 时间复杂度 O(N)：每个节点访问不超过 2 次
  • 空间复杂度 O(logN)：递归栈深度 = 二叉树的高度

执行结果：

  1. 执行结果：通过
  3. 执行用时：28 ms, 在所有 C++ 提交中击败了 32.58% 的用户
  4. 内存消耗：27.1 MB, 在所有 C++ 提交中击败了 26.52% 的用户