leetcode：877. 石子游戏

题目

Alice 和 Bob 用几堆石子在做游戏。一共有偶数堆石子，排成一行；每堆都有正整数颗石子，数目为 piles[i] 。
游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。
Alice 和 Bob 轮流进行，Alice 先开始 。每回合，玩家从行的开始或结束处取走整堆石头。这种情况一直持续到没有更多的石子堆为止，此时手中 石子最多 的玩家获胜。
假设 Alice 和 Bob 都发挥出最佳水平，当 Alice 赢得比赛时返回 true ，当 Bob 赢得比赛时返回 false 。

示例：

输入：piles = [5,3,4,5]
输出：true
解释：
Alice 先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果 Bob 拿走前 3 颗，那么剩下的是 [4,5]，Alice 拿走后 5 颗赢得 10 分。
如果 Bob 拿走后 5 颗，那么剩下的是 [3,4]，Alice 拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对 Alice 来说是一个胜利的举动，所以返回 true 。

输入：piles = [3,7,2,3]
输出：true

解答 & 代码

解法一：递归回溯（超时）

class Solution {
private:
    bool backTrace(vector<int>& files, int start, int end, int cntA, int cntB)
    {
        if(start > end)
            return cntA > cntB;

        return backTrace(files, start + 2, end, cntA + files[start], cntB + files[start + 1]) ||
                backTrace(files, start + 1, end - 1, cntA + files[start], cntB + files[end]) ||
                backTrace(files, start + 1, end - 1, cntA + files[end], cntB + files[start]) ||
                backTrace(files, start, end - 2, cntA + files[end], cntB + files[end - 1]);
    }
public:
    bool stoneGame(vector<int>& piles) {
        return backTrace(piles, 0, piles.size() - 1, 0, 0);
    }
};

解法二：区间 DP

区间动态规划：

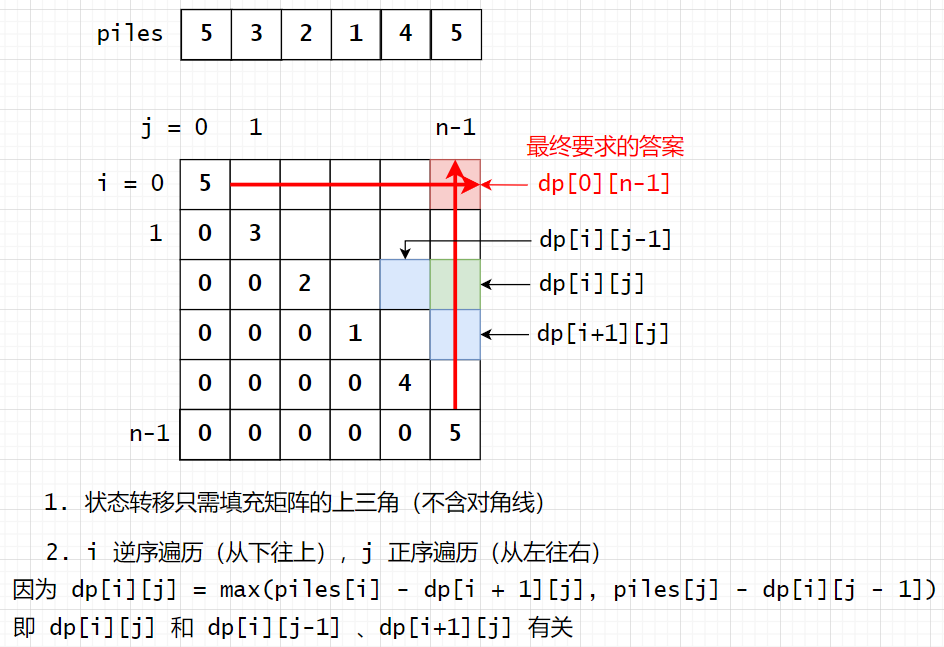
动态规划数组 **dp**：**dp[i][j]** 代表当前剩余第 **[i, j]** 堆石子，当前玩家（本轮取石子的玩家，不一定是全局先手 Alice）和另一个玩家最终的石子数量之差的最大值（只包含从第 [i, j] 堆取的石子）
- 题目最终求的就是 **dp[0][len-1]**，若 **dp[0][len-1] > 0**则说明 Alice 赢，否则 Bob 赢
状态转移方程：dp[i][j] = max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1])
- piles[i] - dp[i + 1][j] 代表当前玩家本轮选择了第 i 堆石子
- piles[j] - dp[i][j - 1] 代表当前玩家本轮选择了第 j 堆石子
初始化：**dp[i][i] = piles[i]**，即只剩下一堆石子时，当前玩家只能取走这堆石子
- 当 i > j 时，dp[i][j] = 0，不过可以不用管这种 case，因为状态转移时用不到这种 case

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        int len = piles.size();
        // dp[i][j] 代表当前剩余第 [i, j] 堆石子，当前玩家（本轮取石子的玩家，不一定是全局先手 Alice）
        // 和另一个玩家最终的石子数量之差的最大值（只包含从第 [i, j] 堆取的石子）
        vector<vector<int>> dp(len, vector<int>(len, 0));
        for(int i = 0; i < len; ++i)            // 初始化
            dp[i][i] = piles[i];

        for(int i = len - 1; i >= 0; --i)        // i 倒序
        {
            for(int j = i + 1; j < len; ++j)    // j 正序
                dp[i][j] = max(piles[i] - dp[i + 1][j],        // 当前玩家本轮选择了第 i 堆石子
                                piles[j] - dp[i][j - 1]);    // 当前玩家本轮选择了第 j 堆石子
        }
        return dp[0][len - 1] > 0;
    }
};

复杂度分析：设有 n 堆石子

时间复杂度：
空间复杂度：

执行结果：

执行结果：通过

执行用时：12 ms, 在所有 C++ 提交中击败了 45.44% 的用户
内存消耗：16 MB, 在所有 C++ 提交中击败了 28.55% 的用户

压缩：由于 dp[i][j] 只和和 dp[i][j-1] 、dp[i+1][j] 有关，即在计算 dp 数组第 i 行的值时，只需用到第 i 行和第 i+1 的值，因此可以用一维 **dp** 数组代替二维 **dp** 数组

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        int len = piles.size();
        vector<int> dp(len);
        for(int i = 0; i < len; ++i)
            dp[i] = piles[i];

        for(int i = len - 1; i >= 0; --i)
        {
            for(int j = i + 1; j < len; ++j)
                dp[j] = max(piles[i] - dp[j],
                            piles[j] - dp[j - 1]);
        }
        return dp[len - 1] > 0;
    }
};

复杂度分析：设有 n 堆石子

时间复杂度：
空间复杂度：压缩为一维 dp 数组

执行结果：

执行结果：通过

执行用时：4 ms, 在所有 C++ 提交中击败了 69.35% 的用户
内存消耗：7.4 MB, 在所有 C++ 提交中击败了 52.58% 的用户

解法三：数学分析

将 n 堆石子分成两组（n 是偶数），偶数下标 0, 2, 4, ..., n-2 的石子堆为 A 组，奇数下标 1, 3, 5, ..., n-1 的石子堆为 B 组。
作为先手的 Alice 可以在第一次取走石子时就决定取走哪一组的石子，并全程取走同一组的石子。因此，只需事先计算 A 组和 B 组的石子总数，Alice 拿总数多的这组石子即可。
解释：初始时 Alice 可以取第 0 堆（A 组）或者第 n - 1 堆（B 组）石子

假设 Alice 开始取第 0 堆石子，也就是 A 组；那么 Bob 只能取第 1 堆或者第 n - 1 堆，都是 B 组；不论 Bob 怎么取，下一轮两端又分别属于 A 组和 B 组，因此 Alice 可以继续选择 A 组的那一堆石子…… 也就是说，Alice 可以全程取走 A 组的石子
假设 Alice 开始取第 n-1 堆石子，也就是 B 组；那么 Bob 只能取第 0 堆或者第 n - 2 堆，都是 A 组；不论 Bob 怎么取，下一轮两端又分别属于 A 组和 B 组，因此 Alice 可以继续选择 A 组的那一堆石子…… 也就是说，Alice 可以全程取走 B 组的石子

因此，Alice 可以全程取走任意一组的石子

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        return true;
    }
};

复杂度分析：

时间复杂度：
空间复杂度：

执行结果：

执行结果：通过

执行用时：0 ms, 在所有 C++ 提交中击败了 100.00% 的用户
内存消耗：7.3 MB, 在所有 C++ 提交中击败了 62.61% 的用户

hot 100

[中等] 877. 石子游戏

题目

解答 & 代码

解法一：递归回溯（超时）

解法二：区间 DP

解法三：数学分析