leetcode：121. 买卖股票的最佳时机

题目

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

解答 & 代码

动态规划（此类题型通用框架）：

动态规划数组 **dp[i][k][0/1]**：代表今天是第 i 天，至今最多进行 k 次交易，今天（最终）手上不持有/持有股票的最大利润
- i 代表今天是第几天，0<=i<=n-1
- k 代表至今最多允许进行的交易次数，1<=k<=K
- 最后一位是持有状态， 0 代表今天最终没有持有股票，1 代表今天最终持有股票
- 题目最终要求的最大利润就是 **dp[n-1][K][0]**（本题中 **K=1**，即求的是 **dp[n-1][1][0]**）
  - n 是天数（即 prices 数组长度）
  - K 是允许的交易次数上限
    - 题目最终要求的最大利润是 dp[n-1][K][0]，而不是 dp[n-1][K][1]，因为后者代表最后一天手上还持有股票，而前者代表最后一天手上没有股票了（没有交易过或已经卖了，至少不会为负数，不会亏），因此前者显然大于后者

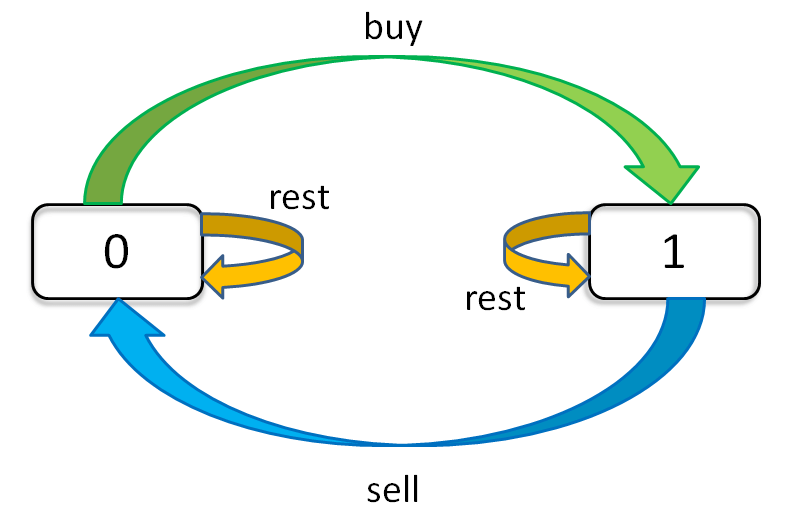
状态转移方程（参照上图的状态机）：
- **dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])**
  - dp[i-1][k][0] 代表今天不交易（rest）
  - dp[i-1][k][1] + prices[i] 代表今天卖出股票（sell）
- **dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])**
  - dp[i-1][k][1] 代表今天不交易（rest）
  - dp[i-1][k-1][0] - prices[i] 代表今天买入股票（buy）
初始化：
- dp[-1][...][0] = 0：第 -1 天还没开始（天数 i 从 0 开始计），因此最大利润为 0
- dp[-1][...][1] = -∞：还没开始，不可能持有股票，因此设为负无穷，使得状态转移方程中取 max 时抛弃这个选项
- dp[...][0][0] = 0：k=0 说明不允许交易，因此最大利润为 0
- dp[...][0][1] = -∞：k=0 代表不允许交易，因此不可能持有股票，因此设为负无穷，使得状态转移方程中取 max 时抛弃这个选项

本题解法：

本题中 K=1，即最终求的是 **dp[n-1][1][0]**
状态转移方程：
- **dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])**
- **dp[i][1][1] = **max(dp[i-1][1][1], dp[i-1][0][0] - prices[i])** = max(dp[i-1][1][1], -prices[i])**
  - 上面“初始化”部分已经解释过，k=0 代表不允许交易，因此最大利润为 0，因此 dp[i-1][0][0]=0
初始化：dp[-1][1][0] = 0，dp[-1][1][1] = -∞

本题中状态转移方程新的状态之和前一天的状态有关，因此不需要数组，直接存储前一天的状态即可

class Solution {
public:
    int maxProfit(vector<int>& prices) {
          // 初始化
        int dp_i_0 = 0;                // 即 dp[i][1][0]
        int dp_i_1 = INT_MIN;        // 即 dp[i][1][1]
          // 状态转移
        for(int i = 0; i < prices.size(); ++i)
        {
              // 今天（第 i 天）最终不持有股票的最大利润，取决于以下两者的最大值
              // - dp_i_0：昨天（第 i-1 天）就没有持有股票，今天休息不操作
              // - dp_i_1 + prices[i]：昨天（第 i-1 天）持有股票，今天卖掉
            dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
              // 今天（第 i 天）最终持有股票的最大利润，取决于以下两者的最大值
              // - dp_i_1：昨天（第 i-1 天）就持有股票，今天休息不操作
              // - -prices[i]：昨天（第 i-1 天）没有持有股票，今天买入
            dp_i_1 = max(dp_i_1, -prices[i]);
        }
        return dp_i_0;
    }
};

复杂度分析：设 prices 数组长度为 N

时间复杂度 O(N)
空间复杂度 O(1)

执行结果：

执行结果：通过
执行用时：92 ms, 在所有 C++ 提交中击败了 88.94% 的用户
内存消耗：91.1 MB, 在所有 C++ 提交中击败了 78.36% 的用户

非模板式解法：
[容易] 121. 买卖股票的最佳时机

hot 100

[简单] 121. 买卖股票的最佳时机

题目

解答 & 代码