题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：
[困难] 42. 接雨水 - 图1

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

输入：height = [4,2,0,3,2,5]
输出：9

本题详见之前的文档：
[困难] 42. 接雨水

解答 & 代码

本题用双指针（left、right）解

柱子 **i** 所在的位置能接雨水的容量：
如下图所示，根据木桶原理，柱子 i 能接水的最大高度取决于柱子 i 左边的最大高度 leftMax 和右边的最大高度 rightMax 的短板 min(leftMax, rightMax) = 2，而柱子 i 本身的高度 height[i] = 1，因此柱子 **i** 所在的位置能接雨水的容量为 **两侧短板高度 - height[i] = 2 - 1 = 1**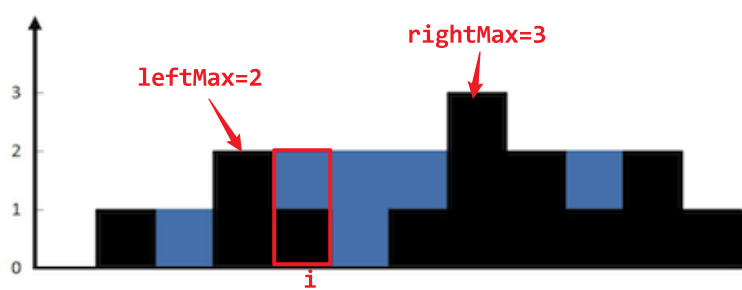

双指针解法：

初始化：
- cap 为题目要求的答案，即能接雨水的总量
- 左指针 left = 0，右指针 right = height.size() - 1
- 左指针及其左边（即 [0, left]）的最大柱子高度 leftMax = 0，右指针及其右边（即 [right, height.size() - 1]）的最大柱子高度 rightMax = 0

遍历 height 数组，即 left、right 收缩的过程

用左指针 left 的高度更新 leftMax，用右指针 right 的高度更新 rightMax
如果 leftMax < rightMax，则计算左指针 left 位置的容量（leftMax - height[left]），加到总容量 cap 上，左指针 left 右移
- 上面分析过一个柱子所在位置能接雨水的容量，left 位置的容量 = left 两侧短板高度 - height[left]。那么就要直到 left 两侧的短板高度：
  - leftMax 是准确的，代表 left 及其左侧（即 [0, left]）的最大柱子高度
  - 而 rightMax 是不准确的，只代表 right 及其右边（即 [right, height.size() - 1]）的最大柱子高度，并不代表 left 右边的最大柱子高度，随着之后 right 往里收缩，rightMax 有可能会变得更大（但至少不会更小）
  - 而当前 leftMax < rightMax，那么短板一定是 leftMax，因为上面提到 rightMax 有可能会变得更大（至少不会更小）

否则，计算右指针 right 位置的容量，右指针 right 左移

分析同上

class Solution {
public:
int trap(vector<int>& height) {
int cap = 0;                                        // 能接雨水的总容量
int left = 0;                                        // 左指针（下标）
int right = height.size() - 1;    // 右指针（下标）
int leftMax = 0;                                // 当前左指针左边最大高度（含当前左指针本身的高度）
int rightMax = 0;                                // 当前右指针右边最大高度（含当前右指针本身的高度）
while(left < right)
{
      // 更新左、右最大高度
    leftMax = max(leftMax, height[left]);
    rightMax = max(rightMax, height[right]);
      // 如果左边最大高度小于右边最大高度，则计算左指针位置的容量，左指针右移
    if(leftMax < rightMax)
    {
          // 对于 left 这根柱子，leftMax 是准确的，rightMax 是不准确的，
          // 因为随着 right 左移，rightMax 还可能变大，而 left 不能再右移（因为讨论的就是 left 这个位置本身）
          // leftMax < rightMax，因此对于 left 这根柱子，其两边界的短板就是 leftMax，
          // 木桶原理，柱子的容量取决于其两遍最大值的短板
        cap += leftMax - height[left];
        ++left;
    }
      // 否则，计算右指针位置的容量，右指针左移
    else
    {
        cap += rightMax - height[right];
        --right;
    }
}
return cap;
}
};

复杂度分析：设 height 数组长为 N

时间复杂度 O(N)
空间复杂度 O(1)

执行结果：

执行结果：通过
执行用时：4 ms, 在所有 C++ 提交中击败了 97.19% 的用户
内存消耗：17.3 MB, 在所有 C++ 提交中击败了 7.36% 的用户