leetcode：581. 最短无序连续子数组

题目

给你一个整数数组 nums ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组，并输出它的长度。

示例：

  1. 输入：nums = [2,6,4,8,10,9,15]
  2. 输出：5
  3. 解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。
  1. 输入：nums = [1,2,3,4]
  2. 输出：0
  1. 输入：nums = [1]
  2. 输出：0

解答 & 代码

解法一：排序

  1. class Solution {
  2. public:
  3.     int findUnsortedSubarray(vector<int>& nums) {
  4.         // 0. 拷贝创建一个数组，并排序
  5.         vector<int> sortedNums = nums;
  6.         sort(sortedNums.begin(), sortedNums.end());
  8.         // 1. 找到最左边的无序位置 left，
  9.         // 即 [0, left) 的元素都在其正确位置，排序后位置不变
  10.         int left = 0;
  11.         while(left < nums.size() && nums[left] == sortedNums[left])
  12.             ++left;
  14.         // 如果 left 越界，说明数组已经是有序的，最短无序连续子数组长度为 0，直接返回
  15.         if(left == nums.size())
  16.             return 0;
  18.         // 2. 找到最右边的无序位置 right，
  19.         // 即 (right, len - 1] 的元素都在其正确位置，排序后位置不变
  20.         int right = nums.size() - 1;
  21.         while(right >= 0 && nums[right] == sortedNums[right])
  22.             --right;
  24.         // 返回 最短无序连续子数组 长度
  25.         return right - left + 1;
  26.     }
  27. };

复杂度分析：设数组长为 N

  • 时间复杂度 O(NlogN)：排序的时间复杂度 O(NlogN)，后序两次遍历寻找 left、right 位置的时间复杂度 O(N)
  • 空间复杂度 O(N)：额外设置了一个等长的数组来存储排序后的数组元素

执行结果：

  1. 执行结果：通过
  3. 执行用时：36 ms, 在所有 C++ 提交中击败了 19.09% 的用户
  4. 内存消耗：26.7 MB, 在所有 C++ 提交中击败了 24.69% 的用户

解法二：两端往里遍历

image.png
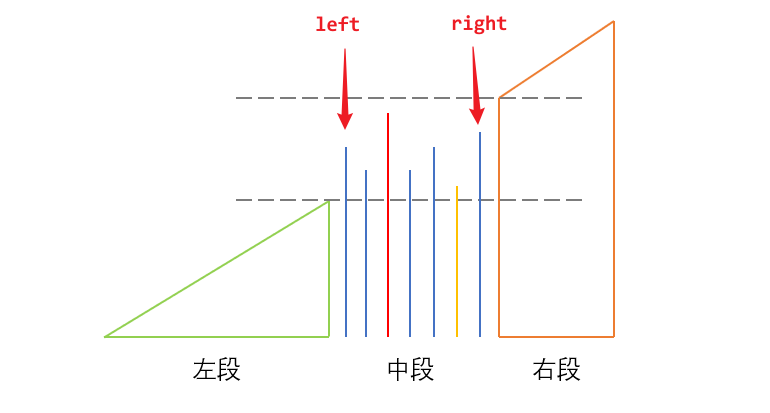
如上图所示，可以将数组分为左、中、右三段，左段和有段都是有序的（单调递增），只有中段是无序的，中段的长度 right - left + 1 就是最短无序连续子数组的长度。因此，我们要找到无序子数组的左边界 left 和右边界 right。

  1. 逆序遍历寻找中段的左边界 **left**：可以发现，左段是有序的，所以左段每个元素都小于其任意一个右侧元素，也就是说左段的每个元素都比其右侧的最小元素小。那么就可以从右往左遍历，实时得到当前位置 i 右侧的最小元素值 rightMin，如果 nums[i] > rightMin，那么 i 肯定在中段，因此更新中段的左边界 left = i。逆序遍历完数组后，最终 left 指向的元素就是最左边一个不满足小于其右侧最小元素的，就是中段的左边界。

  2. 正序遍历寻找中段的右边界 **right**：同理，右段是有序的，所以右段的每个元素都大于其任意一个左侧元素，也就是说右段的每个元素都比其左侧的最大元素大。那么就可以从左往右便利，实时得到当前位置 i 左侧的最大元素值 leftMax，如果 nums[i] < rightMax，那么 i 肯定在中段，因此更新中段的右边界 right = i。 正序遍历完数组后，最终 right 指向的元素就是最右边一个不满足大于其左侧最大元素的，就是中段的右边界。

    1. class Solution {
    2. public:
    3.  int findUnsortedSubarray(vector<int>& nums) {
    4.      int len = nums.size();
    6.      int rightMin = INT_MAX;        // 右侧的最小值
    7.      int left = -1;                // 中段（无序子数组）的左边界
    8.      // 1. 逆序遍历寻找中段的左边界（最左边不满足 小于其右侧最小值 的元素所在的位置）
    9.      for(int i = len - 1; i >= 0; --i)
    10.      {
    11.          // 如果当前元素 nums[i] 不满足小于右侧最小值 rightMin，
    12.          // 说明当前元素位于中段，则更新左边界 left
    13.          if(nums[i] > rightMin)
    14.              left = i;
    15.          // 否则，更新右侧最小值 rightMin
    16.          else
    17.              rightMin = nums[i];
    18.      }
    20.      // 注意：特判：如果数组本身是有序的，遍历完后中段左边界仍为 -1，直接返回 0
    21.      if(left == -1)
    22.          return 0;
    24.      int leftMax = INT_MIN;        // 左侧的最大值
    25.      int right = -1;                // 中段（无序子数组）的右边界
    26.      // 2. 正序遍历寻找中段的右边界（最右边不满足 大于其左侧最大值 的元素所在的位置）
    27.      for(int i = 0; i < len; ++i)
    28.      {
    29.          // 如果当前元素 nums[i] 不满足大于其左侧最大值 leftMax，
    30.          // 说明当前元素位于中段，则更新右边界 right
    31.          if(nums[i] < leftMax)
    32.              right = i;
    33.          // 否则，更新左侧最大值 leftMax
    34.          else
    35.              leftMax = nums[i];
    36.      }
    38.      // 返回中段（最短无序连续子数组）的长度
    39.      return right - left + 1;
    40.  }
    41. };

    复杂度分析：

  • 时间复杂度 O(N)
  • 空间复杂度 O(1)

执行结果：

  1. 执行结果：通过
  3. 执行用时：16 ms, 在所有 C++ 提交中击败了 97.97% 的用户
  4. 内存消耗：25.9 MB, 在所有 C++ 提交中击败了 59.11% 的用户