leetcode：312. 戳气球

题目

有 n 个气球，编号为 0 到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums 中。
现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1 或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。
求所能获得硬币的最大数量。

示例：

  1. 输入：nums = [3,1,5,8]
  2. 输出：167
  3. 解释：
  4. nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
  5. coins =  3*1*5    +   3*5*8   +  1*3*8  + 1*8*1 = 167
  1. 输入：nums = [1,5]
  2. 输出：10

解答 & 代码

只要涉及求最值，没有任何奇技淫巧，一定是穷举所有可能的结果，然后对比得出最值。
因此，只要遇到求最值的算法问题，首先要思考的就是：如何穷举出所有可能的结果？

  • 解法一：回溯算法，就是暴力穷举。
    • 本题就是穷举所有可能的戳破气球的顺序，计算每个顺序对应的分数，找最大值。因此，就是一个全排列问题。但全排列时间复杂度 O(N!)，本题超时
  • 解法二：动态规划，就是根据状态转移方程推到“状态”。

    解法一：递归回溯（超时）

    本题就是穷举所有可能的戳破气球的顺序，计算每个顺序对应的分数，找最大值。因此，就是一个全排列问题。但全排列时间复杂度 O(N!)，本题超时

    nums 数组长为 10 时都能正常运行，长为 11 时超时。

  1. class Solution {
  2. public:
  3.     // 递归回溯函数定义：输入一组气球 nums，返回戳破它们获得的最大分数
  4.     int maxCoins(vector<int>& nums) {
  5.         // 递归结束条件：数组为空 or 只有一个气球
  6.         if(nums.size() == 0)
  7.             return 0;
  8.         if(nums.size() == 1)
  9.             return nums[0];
  11.         int result = 0;        // 结果，戳破 nums 数组的气球能得到的最大分数
  12.         // 遍历气球数组
  13.         for(int i = 0; i < nums.size(); ++i)
  14.         {
  15.             // 以当前气球 nums[i] 作为第一个戳破的气球
  16.             int coin = nums[i];
  17.             // 只戳破当前气球能获得的分数
  18.             int curResult = (i - 1 >= 0 ? nums[i - 1] : 1) * coin * (i + 1 < nums.size() ? nums[i + 1] : 1);
  19.             // a. 做选择：在 nums 数组中删除当前元素 nums[i]
  20.             nums.erase(nums.begin() + i);
  21.             // b. 递归回溯：求剩余数组能获得的最大分数，和戳破当前气球的分数相加
  22.             //    得到先戳破当前气球，再戳破其它所有气球所能获得的最大分数 curResult
  23.             //    并更新全局最大分数 result
  24.             curResult += maxCoins(nums);
  25.             result = max(result, curResult);
  26.             // c. 撤销选择：将删掉的 nums[i] 重新插入 nums 数组第 i 个位置，以撤销改动
  27.             nums.insert(nums.begin() + i, coin); 
  28.         }
  29.         return result;
  30.     }
  31. };

复杂度分析：设 nums 数组长为 N

  • 时间复杂度 O(N!)：递归回溯解法等同于全排列，戳破第一个气球时有 N 个选择，戳破第二个气球时有 N-1 个选择，… …，要遍历完所有可能的情况，时间复杂度是阶乘级别
  • 空间复杂度 O(N)：递归深度 = 数组长度

执行结果：超时

解法二：动态规划

动态规划：

  1. 动态规划数组

    运用动态规划算法的一个重要条件：子问题必须独立。而本题，每戳破一个气球 nums[i]，得到的分数和该气球相邻的气球 nums[i-1] 和 nums[i+1] 是有相关性的。因此，需要想办法定义 dp 数组的含义，避免子问题产生相关性，才能推出合理的状态转移方程

**dp[i][j]** 代表：戳破 **(i, j)** 之间所有气球能得到的最大分数（注意是开区间！戳破 (i, j) 之间所有气球，还剩下气球 i 和气球 j 未戳破）

  • 因为是开区间，所以二维 dp 数组的行数、列数都为 n + 2（设数组 nums 长度为 n）
  • 题目最终要求的是 **dp[0][n + 1]**
  1. 初始化（bad case）

当 **j <= i + 1** 时，**dp[i][j] = 0**。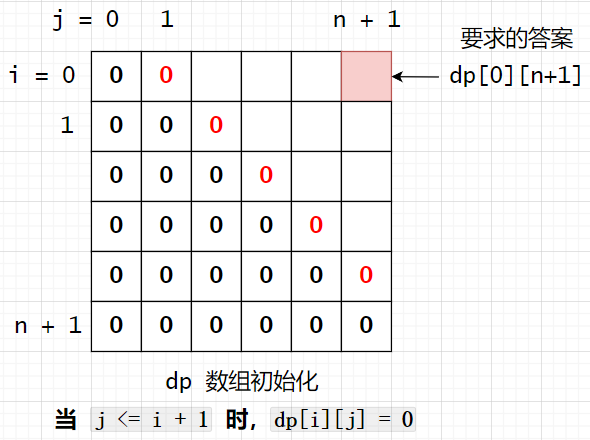
image.png

  1. 状态转移

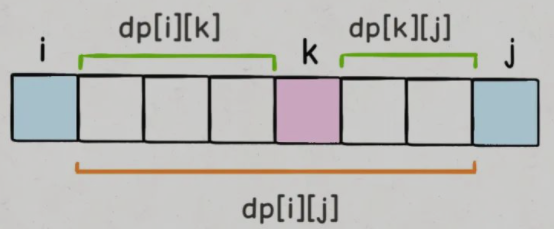
状态转移方程：**dp[i][j] = max(dp[i][k] + dp[k][j] + points[i] * points[k] * points[j])**，其中 **k∈(i, j)**

  • 假设 **k** 是 **(i, j)** 之间最后一个被戳破的气球，那么区间 (i, k) 、 (k, j) 的气球都已经被戳破了。
    • 戳破 (i, k) 之间所有气球的最大分数为 dp[i][k]
    • 戳破 (k, j) 之间所有气球的最大分数为 dp[i][k]
    • 最后戳破气球 k，注意此时和气球 k 相邻的两个气球是 **i** 和 **j**，而不是 k-1、k+1（之前就已经戳破了），因此戳破气球 k 的分数为 points[i] * points[k] * points[j])

image.png

  • 在开区间 (i, j) 遍历所有 k 可能的取值，计算如果最后一个戳破气球 k ，戳破 (i, j) 之间所有气球能得到的最大分数。去所有 `k 对应的最大分数，就是dp[i][j]` 的值

本题还要关注一个问题：进行状态转移时，按什么顺序穷举“状态”？

以下图为例进行说明，先在图中标好 bad case（即初始化）

  • 原则 1：遍历的终点必须是存储结果的位置
    • 如下图所示，本题的结果是 dp[0][n-1]，用红色标出
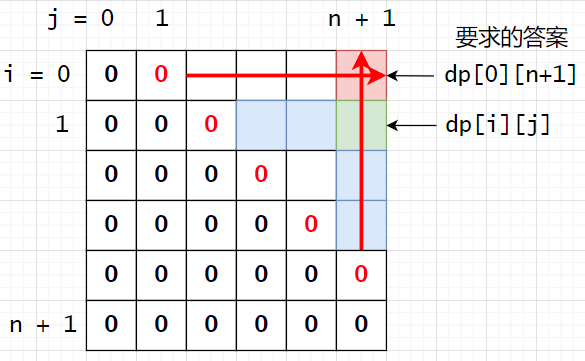
  • 原则 2：遍历的过程中，所依赖的状态必须是已经计算出来的
    • 本题，根据状态转移公式：dp[i][j] = max(dp[i][k] + dp[k][j] + points[i] * points[k] * points[j])，其中 **k∈(i, j)**。也就是说。在计算状态 **dp[i][j]** 时，要求状态** dp[i][k**] 和 **dp[k][j]** 已经计算好。
    • 因此，对于任意的 dp[i][j]，如下图的绿色方块，它的计算依赖于左侧的紫色方块 dp[i][k] 和下方的紫色方块 dp[k][j]，因此本题的遍历方法是 **i** 从下往上遍历（递减），**j** 从左往右遍历（递增）

image.png

  1. class Solution {
  2. public:
  3.     int maxCoins(vector<int>& nums) {
  4.         int len = nums.size();
  5.         // 扩充边界，在数组两侧添加虚拟气球，值为 1
  6.         vector<int> points(len + 2, 1);
  7.         for(int i = 0; i < len; ++i)
  8.             points[i + 1] = nums[i];
  10.         // 1. dp 数组：dp[i][j] 代表戳破 (i, j) 之间所有气球能得到的最大分数
  11.         // 注意是开区间！戳破 (i, j) 之间所有气球，还剩下气球 i 和气球 j 未戳破
  12.         // 2. 初始化（bad case）：当 j <= i + 1 时，dp[i][j] = 0，下面这行语句已顺带初始化
  13.         vector<vector<int>> dp(len + 2, vector<int>(len + 2, 0));
  14.         // 3. 状态转移
  15.         for(int i = len - 1; i >= 0; --i)            // i 应该从下往上遍历
  16.         {
  17.             for(int j = i + 2; j < len + 2; ++j)    // j 应该从左往右遍历
  18.             {
  19.                 // 根据状态转移公式，计算 dp[i][j]
  20.                 for(int k = i + 1; k < j; ++k)        // 枚举 k in [i + 1, j - 1]
  21.                 { 
  22.                     dp[i][j] = max(dp[i][j], 
  23.                                dp[i][k] + dp[k][j] + points[i] * points[k] * points[j]);
  24.                 }
  25.             }
  26.         }
  28.         // 返回结果
  29.         return dp[0][len + 1];
  30.     }
  31. };

复杂度分析：设 nums 数组长为 N

  • 时间复杂度 [困难] 312. 戳气球 - 图4：三重循环：二维 dp 数组状态数 [困难] 312. 戳气球 - 图5，状态转移（即遍历 k）时间复杂度 O(N)
  • 空间复杂度 [困难] 312. 戳气球 - 图6：二维 dp 数组
  1. 执行结果：通过
  3. 执行用时：384 ms, 在所有 C++ 提交中击败了 83.86% 的用户
  4. 内存消耗：10.1 MB, 在所有 C++ 提交中击败了 20.55% 的用户