B树
B树又叫做二叉搜索树,倒状的树形结构。如下图所示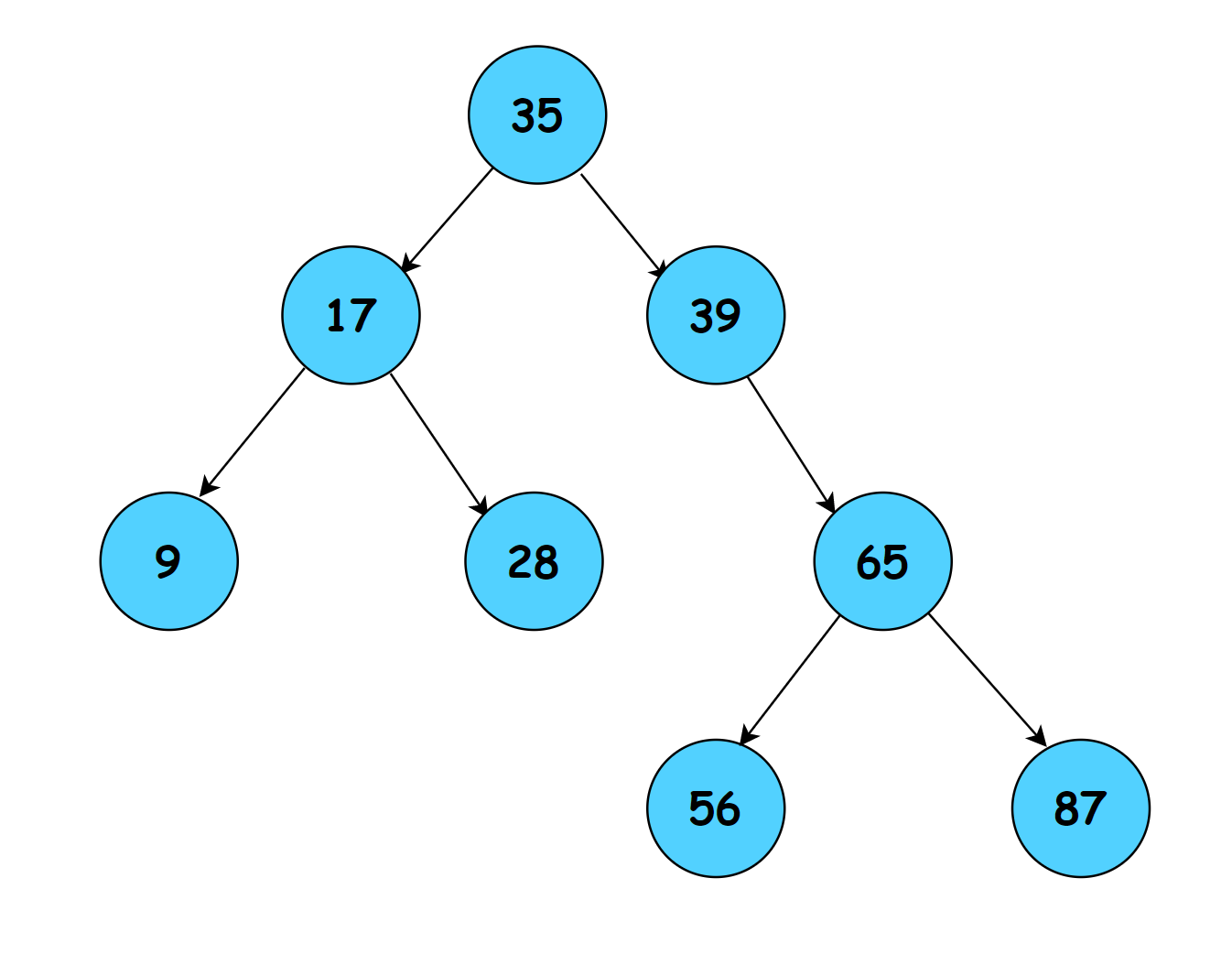
特点:
- 所有的非子夜节点最多拥有两个子节点树(左子树和右子树)。
- 所有结点存储一个关键字。
- 节点的左右儿子,左边是比该节点小的,右边是比该节点大的。
缺点:
因为二叉搜索树不存在平衡算法,所以在某些特殊的情况下,二叉搜索树等同于线性,出现蹩脚的情况,设计者们发现降低树的高度自然就可以提高查找效率。那么如何解决降低树的高度的问题?在这种基础上设计者给二叉树加入了平衡算法,出现了平衡树。
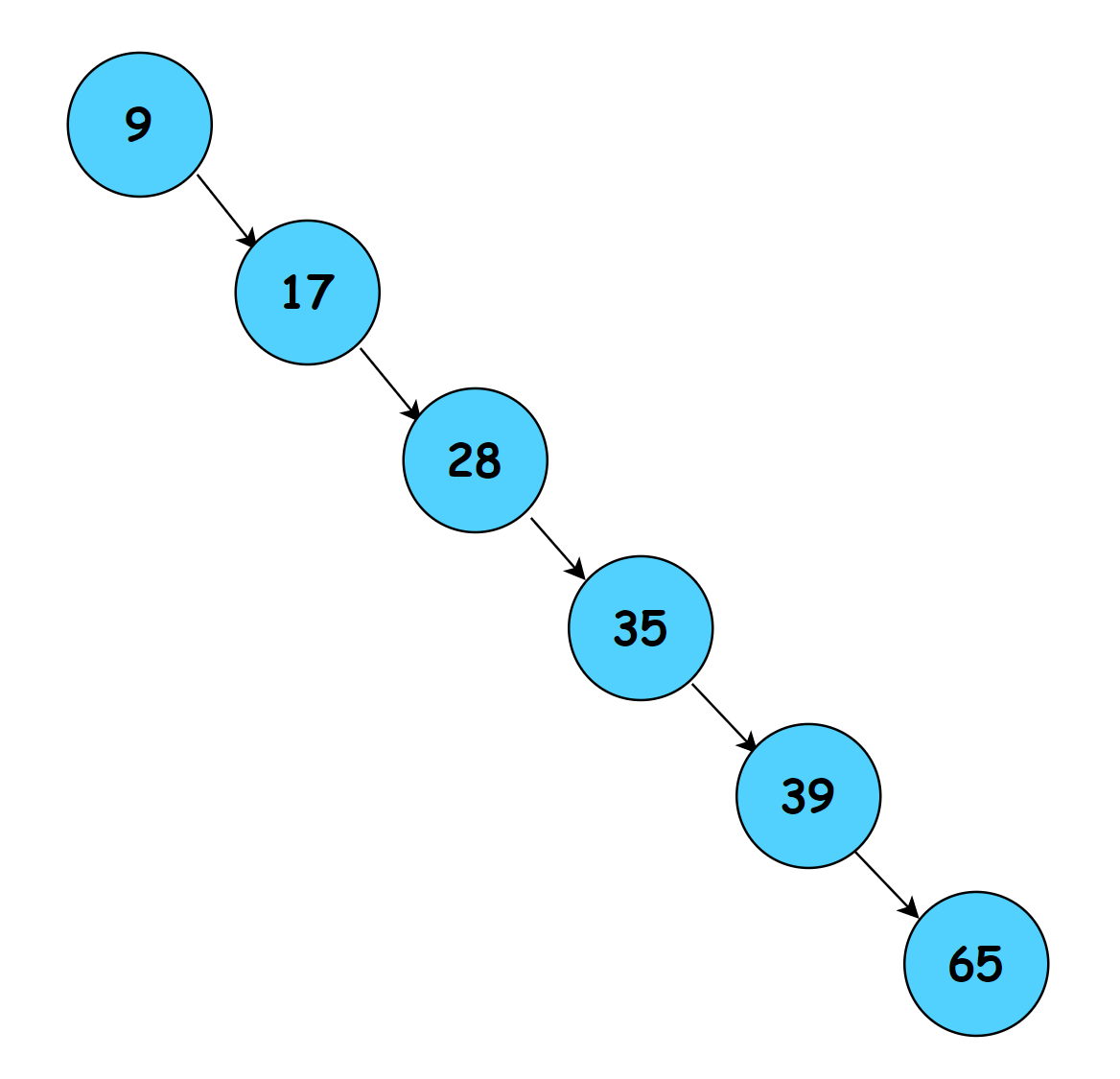
二叉树搜索树的查询原理,先从根节点开始,和根节点匹配,若是比根节点小就进入左子节点,若是比根节点大进行右子节点,依次按照这样的逻辑进行,找到就返回。
另一方面树的高度也会影响查询的效率,设计者又是怎么解决的呢? 假设大规模数据存储中,实现索引查询这样一个实际背景下,树节点存储的元素数量是有限的,即使存储在平衡二叉树中,在大量数据的储存情况下,这样导致二叉平衡查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下,那么如何减少树的深度(当然是不能减少查询的数据量),一个基本的想法就是:采用多叉树结构(由于树节点元素数量是有限的,自然该节点的子树数量也就是有限的)。在这种前提下,B-、B+、B*也就是这样的数据结构,多路搜索树,不再是只有二路。
所谓的平衡就是加上平衡算法,在B树在经过多次插入与删除后,有可能导致不同的结构,极端一点就是出现线性的蹩脚树,通过平衡算法(左旋和右旋),使树的节点分布均匀,是树的查找算法等同于二分查找。所以对于树而言要提高查找的效率,一个是保存平衡;另一个是减少树的高度。
B-树
基于减少树的高度上,B-树是一种多路搜索树,并不是二叉的。如下图所示: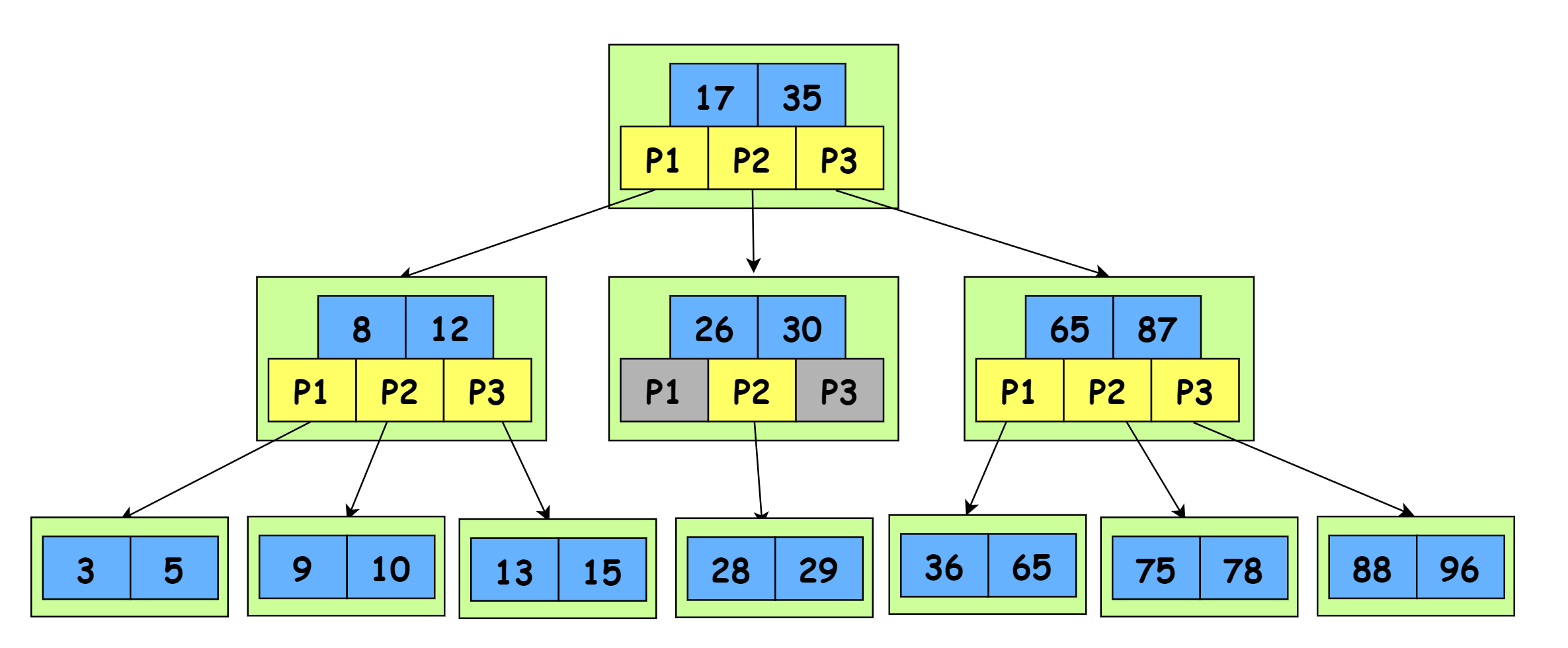
特点:
- 所有的非叶子结点最多有M个儿子(且M>2)。
- 根结点的儿子数为[2, M],其它非叶子结点的儿子数为[M/2, M]。
- 每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)。
- 非叶子结点的关键字个数=指向儿子的指针个数-1。
- 非叶子结点的关键字中从左到右由大到小排序。即A[1]
- 非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])范围的子树,最后一个指针P[M]指向大于随后一个关键字A[M-1]范围的值。
- 关键字集合分布在整颗树中,并且只会在节点中出现一次。
- 搜索可能在非子叶节点或者子叶节点结束,即非子叶节点也存储数据的身,这个与B+树有根本区别。
- 所有叶子结点位于同一层。
缺点:
- 当数据量大的时候不是依然会查询到最底层的叶子节点。这就是B-树的缺点,但是相比B树而言已经优化了很多。
B-树的性能总是等价于二分查找(与M值无关),也就没有B树平衡的问题。由于M/2的限制,在插入结点时,如果结点已满,需要将结点分裂为两个各占M/2的结点;删除结点时,需将两个不足M/2的兄弟结点合并。
B+树
B+树是B-树的变体,也是一种多路搜索树。如下图所示:
B+基本与B-树同,以下是与B-树的区别:
- 非叶子结点的指针与关键字个数相等,而B-树的关键字=指针个数-1;
- 指针P[i],指向关键字值属于[K[i], K[i+1])范围的子树,而在B-树是开区间。
- 所有叶子结点增加一个指针,指向下一个的兄弟叶子节点。
- 所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的,搜索只会在叶子节点结束,叶子节点存储所有关键字的值。
- 不可能在非叶子结点命中;非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储。
B树与B+树的区别:
- 所有的叶子节点包含了全部关键子信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。(而B树的叶子节点并没有包括全部需要查找的信息)。
- 所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。(而B树的非终节点也包含需要查找的有效信息)。
这些链指针在链表中是有序存储的,在搜索中能省大量的时间。那这些链指针可不可以加在所有的节点中呢,答案是可以的,除了根节点,所有的节点都可以加上链指针。这就是B*树索引。
B*树
B*树是在B+树的基础上,在B+树的非根和非叶子结点增加指向兄弟的指针,将结点的最低利用率从1/2提高到2/3。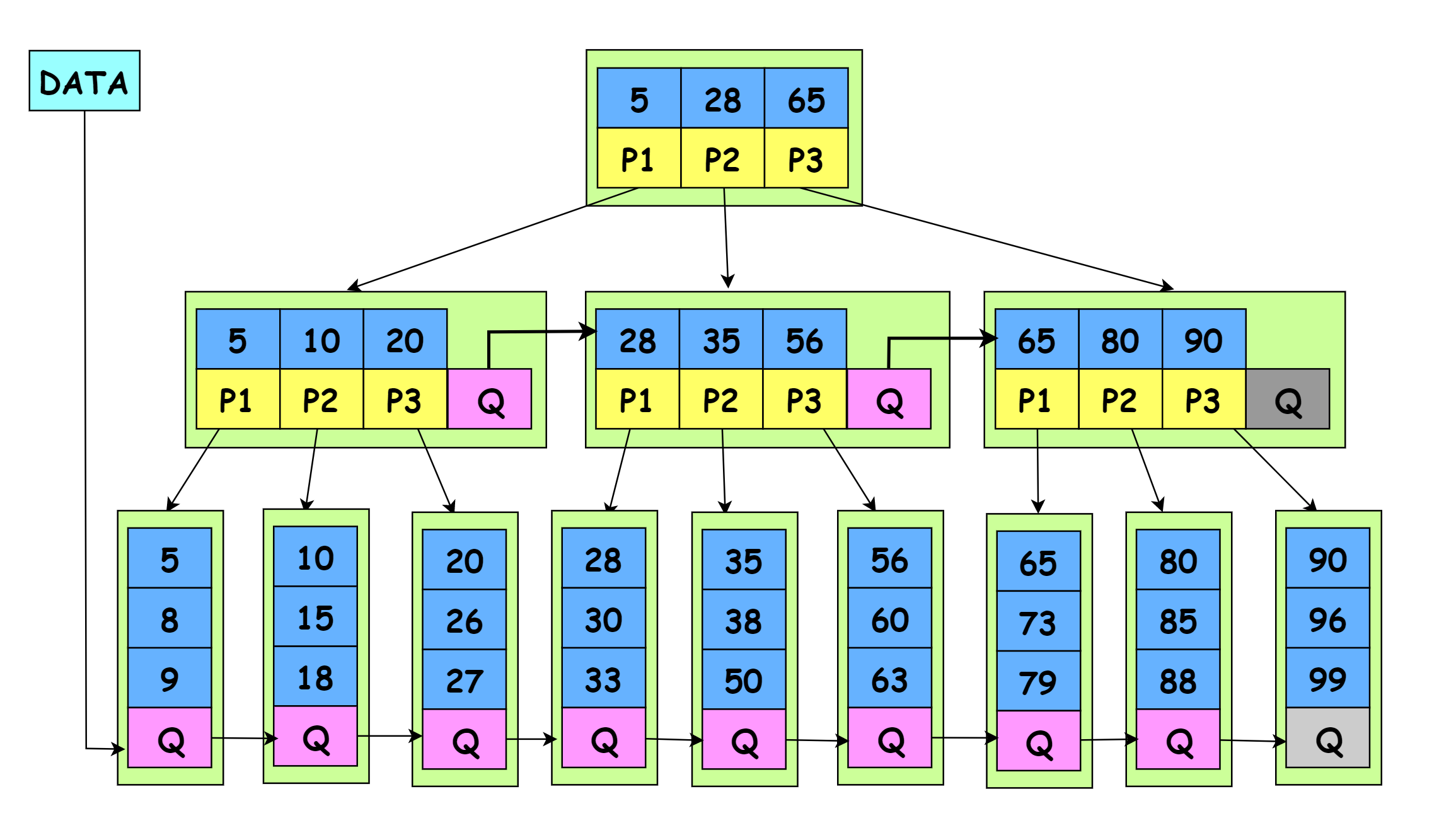
特点:
- B*树定义了非叶子结点关键字个数至少为(2/3)M,即块的最低使用率为2/3(代替B+树的1/2)
- 在非根和非叶子结点增加指向兄弟的指针。
B+树与B树的区别: (1)B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针。 (2)B树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针。 结论: 所以,B*树分配新结点的概率比B+树要低,空间使用率更高。
关于回表查询:
比如select name from table where id=?,如果name没有索引,那在查询的时候先得得到的是id对应这条数据所在的行数。拿着这个行数,再去表中查询这条数据,得到name字段。而拿着这个行数去得到name字段的动作,就是回表查询。

