RedisJava

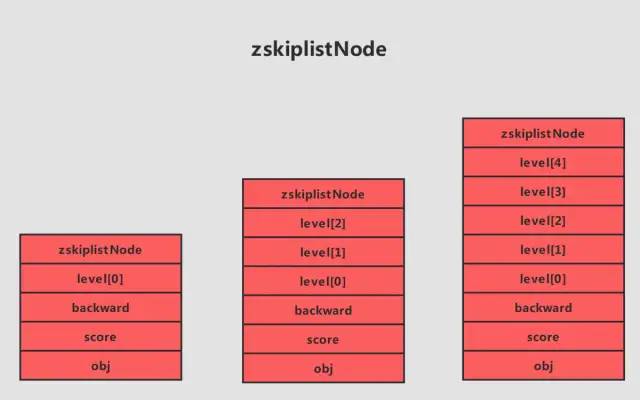
跳跃表

跳跃表是一种有序的随机数据结构。
它通过在每个节点中维持多个指向其他节点的指针，从而快速达到访问节点的目的。

什么是跳跃表 ？

对于一个单链表来说， 即便链表中存储的数据是有序的， 想要随机查找一个数据，那么也只能从头到尾遍历链表节点， 这样查找的效率就会很低，是件复杂度为 O(n)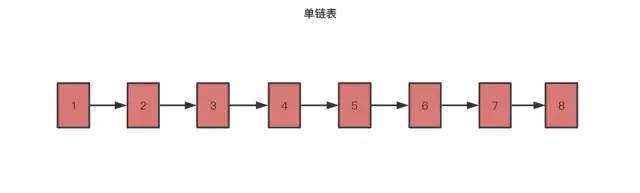
跳跃表基本原理和 Java实现 - 图1
如果想要提高其查找效率， 可以考虑在链表上建索引的方式。每2个节点提取一个节点到上一级，把抽出来的那一级叫作索引。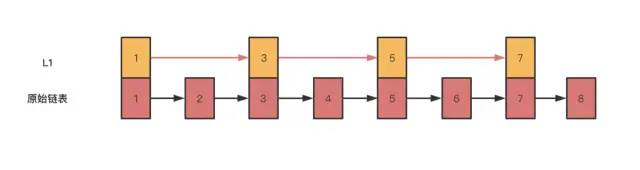
跳跃表基本原理和 Java实现 - 图2
这个时候，假设 要查找节点8 ，可以先在索引层遍历， 当遍历到索引层中7节点时，发现下一个节点是9， 那么要查询的节点8 一定在 7和9节点之间， 下降到 原始链表层，继续遍历就找到了8这个节点， 原来在单链表中要找到8这个节点要遍历8个节点，而现在有了一层索引后只需要遍历5个节点即可。
从上面例子里可以看出， 加了一层索引以后， 查找一个节点需要遍历的节点数少了， 也就是说查找效率提升了，同理可以再加一层索引。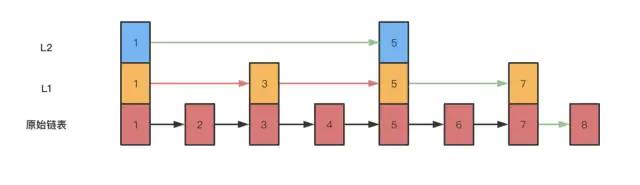
跳跃表基本原理和 Java实现 - 图3
从图中可以看出，查找效率又有提升。在例子中数据很少，当有大量的数据时，可以增加多级索引，其查找效率可以得到明显提升。
像这种链表加多级索引的结构，就是跳跃表!

Redis跳跃表

Redis使用跳跃表作为有序集合键的底层实现之一,如果一个有序集合包含的元素数量比较多,又或者有序集合中元素的成员是比较长的字符串时, Redis就会使用跳跃表来作为有序集合健的底层实现。
这里需要思考一个问题——为什么元素数量比较多或者成员是比较长的字符串的时候Redis要使用跳跃表来实现？
从上面可以知道，跳跃表在链表的基础上增加了多级索引以提升查找的效率，但其是一个空间换时间的方案，必然会带来一个问题——索引是占内存的。原始链表中存储的有可能是很大的对象，而索引结点只需要存储关键值值和几个指针，并不需要存储对象，因此当节点本身比较大或者元素数量比较多的时候，其优势必然会被放大，而缺点则可以忽略

Redis中跳跃表的实现

Redis的跳跃表由zskiplistNode和skiplist两个结构定义,其中 zskiplistNode结构用于表示跳跃表节点,而 zskiplist结构则用于保存跳跃表节点的相关信息,比如节点的数量,以及指向表头节点和表尾节点的指针等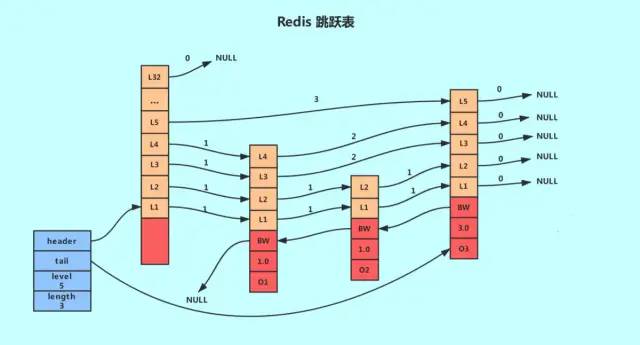
跳跃表基本原理和 Java实现 - 图4

  • header:指向跳跃表的表头节点，通过这个指针程序定位表头节点的时间复杂度就为O(1)
  • tail:指向跳跃表的表尾节点,通过这个指针程序定位表尾节点的时间复杂度就为O(1)
  • level:记录目前跳跃表内,层数最大的那个节点的层数(表头节点的层数不计算在内)，通过这个属性可以再O(1)的时间复杂度内获取层高最好的节点的层数。
  • length:记录跳跃表的长度,也即是,跳跃表目前包含节点的数量(表头节点不计算在内)，通过这个属性，程序可以再O(1)的时间复杂度内返回跳跃表的长度。

结构右方的是四个 zskiplistNode结构,该结构包含以下属性:

  • 层(level):
    节点中用1、2、L3等字样标记节点的各个层,L1代表第一层,L代表第二层,以此类推。
    每个层都带有两个属性:前进指针和跨度。前进指针用于访问位于表尾方向的其他节点,而跨度则记录了前进指针所指向节点和当前节点的距离(跨度越大、距离越远)。在上图中,连线上带有数字的箭头就代表前进指针,而那个数字就是跨度。当程序从表头向表尾进行遍历时,访问会沿着层的前进指针进行。
    每次创建一个新跳跃表节点的时候,程序都根据幂次定律(powerlaw,越大的数出现的概率越小)随机生成一个介于1和32之间的值作为level数组的大小,这个大小就是层的“高度”。
  • 后退(backward)指针：
    节点中用BW字样标记节点的后退指针,它指向位于当前节点的前一个节点。后退指针在程序从表尾向表头遍历时使用。与前进指针所不同的是每个节点只有一个后退指针，因此每次只能后退一个节点。
  • 分值(score):
    各个节点中的1.0、2.0和3.0是节点所保存的分值。在跳跃表中,节点按各自所保存的分值从小到大排列。
  • 成员对象(oj):
    各个节点中的o1、o2和o3是节点所保存的成员对象。在同一个跳跃表中,各个节点保存的成员对象必须是唯一的,但是多个节点保存的分值却可以是相同的:分值相同的节点将按照成员对象在字典序中的大小来进行排序,成员对象较小的节点会排在前面(靠近表头的方向),而成员对象较大的节点则会排在后面(靠近表尾的方向)。
    在比较的时候 如果分值相同则会比较保存的对象。

跳跃表基本原理和 Java实现 - 图5

简单跳跃表 JAVA 实现

  1. public class SkipNode<T> {
  2.     // 数据区
  3.     public Integer score;
  4.     public T value;
  6.     // 当前节点的 上下左右层级节点
  7.     public SkipNode up;
  8.     public SkipNode down;
  9.     public SkipNode left;
  10.     public SkipNode right;
  12.     public SkipNode(Integer score, T value) {
  13.         this.score = score;
  14.         this.value = value;
  15.     }
  16. }
  18. public class SkipList {
  19.     // 节点数量
  20.     public int num;
  22.     // 最高层数
  23.     public int max_hight;
  25.     public SkipNode head;
  26.     public SkipNode tail;
  28.     // 概率随机
  29.     private Random random;
  31.     public SkipList() {
  32.         this.max_hight = 6; // 设置最高层数为6层
  33.         this.num = 0; // 初始化时没有节点 这里设置 0
  34.         this.head = new SkipNode(Integer.MIN_VALUE, null);
  35.         this.tail = new SkipNode(Integer.MAX_VALUE, null);
  36.         this.random = new Random();
  37.         this.head.right = tail; // 将链表 头节点与尾节点关联
  38.         this.tail.left = head;
  39.     }
  41.     /**
  42.     * 基本操作   增加， 删除， 查找
  43.     * 但是 这些操作都离不开 查询， 首先要定位到数据 然后再进行 其他操作
  44.     */
  46.     // 查找 , 根据指定的分数值查找数据
  47.     private SkipNode find(Integer score) {
  48.         SkipNode start = this.head;
  49.         while (true) {
  50.             // 如果当前 节点的右节点 score 比要查询的小则 往右移动， 直到遇见比它大的
  51.             // 这里进来会一直往右去找
  52.             while (start.right.score <= score) {
  53.                 start = start.right;
  54.             }
  56.             // 如果已经定位到 当前这一层 右节点比要查询的大了 ， 那么将向下定位 ，这里判断下一层是否为null 不为null 则继续定位
  57.             if (start.down != null) {
  58.                 start = start.down;
  59.             } else {
  60.                 break;
  61.             }
  62.         }
  63.         return start;  // 注意 这里 start.score 分值是小雨等于 传入的 score 值
  64.         // 注意 这里 是小于等于 score值 ，右2种情况
  65.         // 1 如果查找的分值 存在，则返回该对象的底层节点；
  66.         // 2 如果查找的分值 不存在 ，则返回 最接近该对象的底层节点
  67.     }
  69.     // get操作 这里就可以获取 传入分数对应的节点， 如果完全匹配 那么返回该节点对应的value ， 不匹配 则 return null;
  70.     public Object get(Integer score) {
  71.         if (num < 1) {
  72.             return null;
  73.         }
  74.         SkipNode mark = find(score);
  75.         if (mark.score.equals(score)) {
  76.             return mark.value;
  77.         } else {
  78.             return null;
  79.         }
  80.     }
  82.     public void put(Integer score, Object value) {
  83.         // 寻找对应的 分值，如果不存在 则返回最近位置的分值 ，等于已经找到合适的插入位置
  84.         SkipNode mark = find(score);
  85.         // 如果找的节点分值 与要穿入的 相等 那么表示已存在，则进行更新
  86.         if (mark.score.equals(score)) {
  87.             mark.value = value;
  88.             return;
  89.         }
  90.         // 否则 进行插入
  91.         SkipNode brand_new = new SkipNode<>(score, value);
  92.         // 要在 查询到的 mark 右边进行插入，
  93.         // 即 新增的 节点 左边为 查询到的mark。  右边为 原来mark 的右边节点
  94.         brand_new.left = mark;
  95.         brand_new.right = mark.right;
  96.         // 原来 mark 右边节点的左节点更新为 新创建的节点。  将mark 的右节点 更新为 新创建的节点
  97.         mark.right.left = brand_new;
  98.         mark.right = brand_new;
  100.         // 使用变量标识 层级
  101.         int i = 0;
  102.         while (random.nextDouble() < 0.5) {
  103.             if (i > max_hight) {
  104.                 break;
  105.             }
  106.             // 这里 mark 在查询到的时候 已经是最下层 包含所有节点的 那一层的数据了， 然后这里 获取它的上层，看是否存在更高层
  107.             // 如果不存在，那么就切换到左边一个节点继续便利， 一直到获取到存在最高层的 节点
  108.             while (mark.up == null) {
  109.                 mark = mark.left;
  110.             }
  111.             // 找到左侧存在的高层节点
  112.             mark = mark.up;
  113.             // 设置为 新创建的节点的上层节点的 左节点
  114.             // 只有最底层的节点 保存 value ，其他节点只保存 分值即可
  115.             SkipNode up_new = new SkipNode<>(score, null);
  116.             up_new.left = mark;
  117.             up_new.right = mark.right;
  118.             mark.right.left = up_new;
  119.             mark.right = up_new;
  121.             up_new.down = brand_new;
  122.             brand_new.up = up_new;
  124.             // 将当前 全新引用 指向 新创建的 上层的 引用， 如果 while 继续循环，那么 mark 也 已经是 up， 上层的了
  125.             brand_new = up_new;
  126.             ++i;
  127.         }
  128.         ++num;
  129.     }
  131.     public boolean remove(Integer score) {
  132.         SkipNode mark = find(score);
  133.         // 如果 查询到的mark 的 score 与传入的 不同， 表示 根本不存在对应的分值对象， 只是返回了最接近的一个
  134.         if (!mark.score.equals(score)) {
  135.             return true;
  136.         }
  138.         // 查询到的mark 一定是 最底层的链表， 那么就是从最底层开始向上解除关联即 链表删除
  139.         SkipNode del;
  140.         while (mark != null) {
  141.             del = mark.up;
  142.             mark.left.right = mark.right;
  143.             mark.right.left = mark.left;
  144.             // 升一层 如果不为nul 继续处理
  145.             mark = del;
  146.         }
  147.         return true;
  148.     }
  149. }