Q：SVM 可以求解非线性问题吗？
A： 仅在部分数据集中可以

SVM 处理非线性问题理解：
(1) 利用核函数
(2) 软间隔和正则化
利用 SVM 处理非线性问题主要用到了两种方法：
到更高维度去找可以分类的超平面。
有限制地降低分类要求。
当然，这两种方法可以结合使用来达到更好的效果。

image.png

基本概念

SVM 定义

支持向量机是一种二分类模型

image.png

支持向量机分类

image.png
根据不同的数据学习不同类型的支持向量机

函数间隔

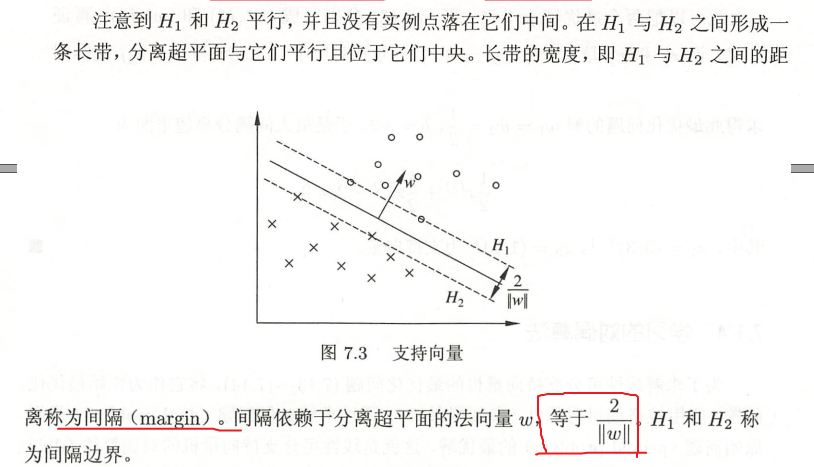
image.png

几何间隔

image.png

最大间隔分离超平面

image.png
image.png

线性可分支持向量机

问题构造

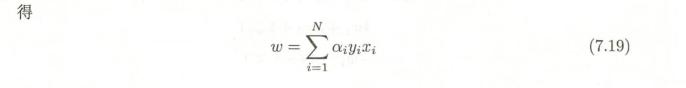
image.png

求解

image.png
image.png
image.pngimage.png
image.png
最终求解得

image.png

支持向量

image.png

线性支持向量机

问题构造

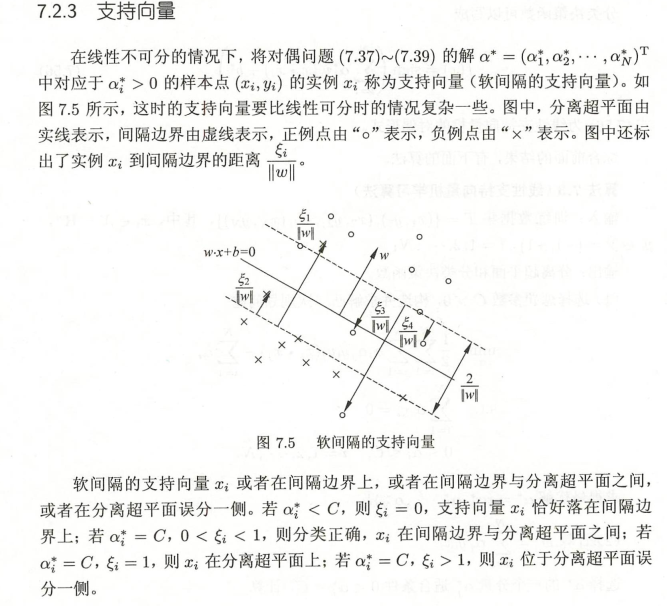
image.png

求解

image.png
image.png

image.png

支持向量

image.png

非线性支持向量机

image.png

支持向量机优缺点

支持向量机的优点是:

  1. 由于 SVM 是一个凸优化问题，所以求得的解一定是全局最优而不是局部最优。
  2. 不仅适用于线性线性问题还适用于非线性问题 (用核技巧)。
  3. 拥有高维样本空间的数据也能用 SVM，这是因为数据集的复杂度只取决于支持向量而不是数据集的维度，这在某种意义上避免了 “维数灾难”。
  4. 理论基础比较完善 (例如神经网络就更像一个黑盒子)。

支持向量机的缺点是:

  1. 二次规划问题求解将涉及 m 阶矩阵的计算 (m 为样本的个数), 因此 SVM 不适用于超大数据集。(SMO 算法可以缓解这个问题)
  2. 只适用于二分类问题。(SVM 的推广 SVR 也适用于回归问题；可以通过多个 SVM 的组合来解决多分类问题)