激活函数

参考

numpy 写激活函数代码：

• https://github.com/ddbourgin/numpy-ml/tree/master/numpy_ml/neural_nets/activation

激活函数可视化（中英文）

• https://dashee87.github.io/deep%20learning/visualising-activation-functions-in-neural-networks/
• https://www.jithub.cn/fileserver/activation_function_all_in_one.html

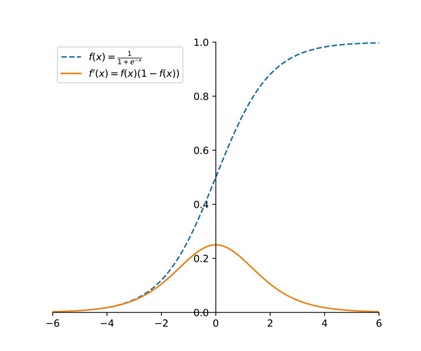
sigmoid

优点

Sigmoid函数具有非常好的可解释性，模拟了一个神经元在随着输入不断增加时从完全不激活到完全激活的过程，符合生物学上的原理，因此在神经网络的早期研究中被广泛使用。

缺陷

其一是函数的两端是饱和区，饱和区内梯度接近于0，会带来熟知的梯度消失问题。
一旦神经元的初始或者优化进入了饱和区域，将难以继续优化。另一方面，随着网络层数的增加，由于链式法则连乘的Sigmoid导数也会变得越来越小，导致梯度难以回传，这会降低网络的收敛速度，甚至导致网络不能收敛到好的状态。
其二是Sigmoid函数的输出值并不是以0为中心，即总是大于0，而权重参数的梯度与输入有关，这就会造成反向传播时一个样本的某一个权重的梯度总是同一个符号，这不利于权重的更新。

tanh

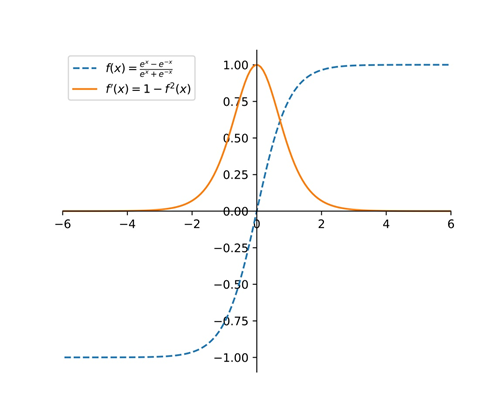
Tanh的导数区间在[0,1]区间，比Sigmoid函数的导数区间要大，在反向传播过程中，衰减速度要比Sigmoid慢，然而梯度消失的问题和幂运算的问题仍然存在。

relu

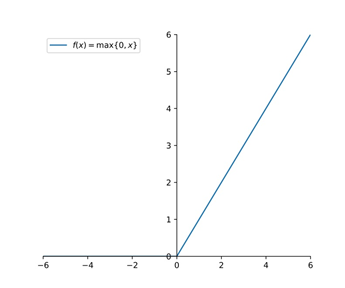
ReLU函数本质是一个取最大值函数，非全区间可导，但是在计算过程中可以取近似梯度。在x>0时，梯度为1，小于等于0时，梯度为0。

ReLU在正区间内解决了梯度消失问题，只需要判断输入是否大于0，所以计算速度非常快，收敛速度远快于Sigmoid和Tanh函数。

总结

sigmoid 和 tanh 幂运算和梯度消失的问题
sigmoid 不以 0 为中心
relu 解决了梯度消失的问题